Trójkąty równoboczne 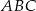 i
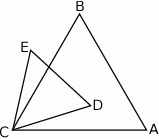
i 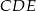 są położone tak, jak na poniższym rysunku. Wykaż, że
są położone tak, jak na poniższym rysunku. Wykaż, że 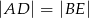 .
.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Trójkąty równoboczne 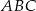 i
i 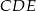 są położone tak, jak na poniższym rysunku. Wykaż, że
są położone tak, jak na poniższym rysunku. Wykaż, że 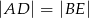 .
.

Na ramionach 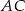 i
i 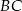 trójkąta równoramiennego
trójkąta równoramiennego 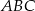 wybrano punkty
wybrano punkty 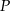 i
i 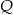 w ten sposób, że odcinek
w ten sposób, że odcinek 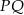 jest równoległy do podstawy
jest równoległy do podstawy 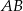 i styczny do okręgu wpisanego w trójkąt
i styczny do okręgu wpisanego w trójkąt 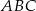 . Wykaż, że pole trójkąta
. Wykaż, że pole trójkąta 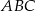 jest równe
jest równe
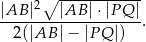
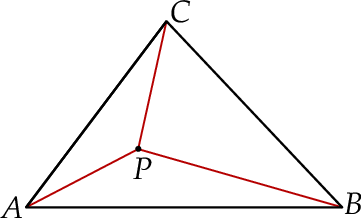
Każdy kąt trójkąta 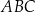 ma miarę mniejszą od
ma miarę mniejszą od 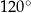 . Wyznacz taki punkt
. Wyznacz taki punkt 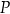 wewnątrz trójkąta
wewnątrz trójkąta 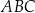 , dla którego suma
, dla którego suma 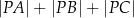 jest najmniejsza możliwa.
jest najmniejsza możliwa.
Na okręgu o promieniu  opisano trapez, w którym
opisano trapez, w którym 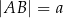 i
i 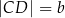 .
.
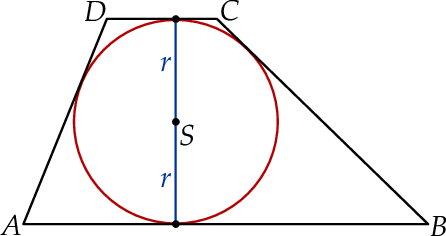
Wykaż, że 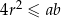 .
.
W trapezie 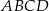 połączono środek
połączono środek 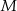 ramienia trapezu
ramienia trapezu 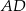 z końcami drugiego ramienia
z końcami drugiego ramienia 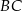 . Wykaż, że pole powstałego trójkąta
. Wykaż, że pole powstałego trójkąta 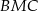 jest równe połowie pola trapezu
jest równe połowie pola trapezu 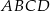 .
.
Punkt 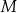 jest środkiem boku
jest środkiem boku 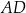 . Udowodnij, że pole trójkąta
. Udowodnij, że pole trójkąta 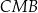 jest połową pola trapezu
jest połową pola trapezu 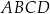 (
(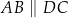 ).
).

Z punktu 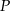 należącego do boku
należącego do boku 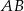 trójkąta równobocznego
trójkąta równobocznego 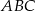 poprowadzono półprostą dzielącą trójkąt na dwie figury o równych polach. Oblicz tangens kąta jaki tworzy ta półprosta z odcinkiem
poprowadzono półprostą dzielącą trójkąt na dwie figury o równych polach. Oblicz tangens kąta jaki tworzy ta półprosta z odcinkiem 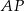 , jeśli
, jeśli 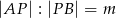 i
i 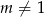 .
.
Dane są dwa półokręgi o wspólnym środku 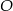 i średnicach odpowiednio
i średnicach odpowiednio 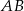 i
i 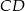 (punkty
(punkty 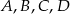 i
i 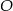 są współliniowe).
są współliniowe).
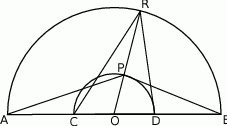
Punkt 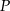 leży na wewnętrznym półokręgu, punkt
leży na wewnętrznym półokręgu, punkt 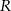 leży na zewnętrznym półokręgu, punkty
leży na zewnętrznym półokręgu, punkty 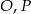 i
i 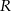 są współliniowe. Udowodnij, że
są współliniowe. Udowodnij, że 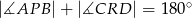 .
.
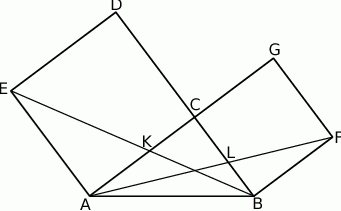
Na przyprostokątnych 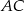 i
i 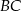 trójkąta prostokątnego
trójkąta prostokątnego 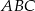 zbudowano, na zewnątrz trójkąta, kwadraty
zbudowano, na zewnątrz trójkąta, kwadraty 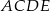 i
i 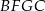 . Odcinek
. Odcinek 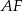 przecina przyprostokątną
przecina przyprostokątną 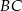 w punkcie
w punkcie 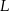 , a odcinek
, a odcinek 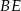 przecina przyprostokątną
przecina przyprostokątną 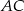 w punkcie
w punkcie 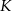 (zobacz rysunek). Udowodnij, że
(zobacz rysunek). Udowodnij, że 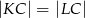 .
.
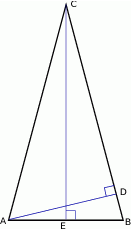
W trójkącie równoramiennym 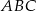 , w którym
, w którym 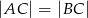 wysokość
wysokość 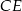 jest dwa razy dłuższa od wysokości
jest dwa razy dłuższa od wysokości 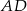 (patrz rysunek). Oblicz kosinusy wszystkich kątów wewnętrznych trójkąta
(patrz rysunek). Oblicz kosinusy wszystkich kątów wewnętrznych trójkąta  .
.
W trójkącie równobocznym  o wysokości
o wysokości 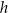 obrano punkt
obrano punkt 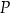 , z którego poprowadzono odcinki prostopadłe do boków tego trójkąta. Wykaż, że suma długości tych odcinków jest równa
, z którego poprowadzono odcinki prostopadłe do boków tego trójkąta. Wykaż, że suma długości tych odcinków jest równa 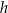 .
.
Wykaż, że trójkąt, którego długości boków są trzema kolejnymi wyrazami ciągu geometrycznego, miary kątów zaś trzema kolejnymi wyrazami ciągu arytmetycznego jest trójkątem równobocznym.
Na przyprostokątnych 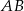 i
i 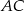 trójkąta prostokątnego równoramiennego
trójkąta prostokątnego równoramiennego 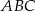 zaznaczono odpowiednio punkty
zaznaczono odpowiednio punkty 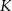 i
i 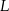 tak, że
tak, że 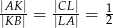 . Odcinki
. Odcinki 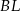 i
i 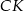 przecinają się w punkcie
przecinają się w punkcie 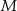 . Oblicz
. Oblicz 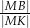 .
.
Wykaż, że jeżeli długości 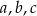 boków trójkąta spełniają równość
boków trójkąta spełniają równość
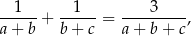
to promień okręgu opisanego na tym trójkącie jest równy 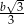 .
.
Wewnątrz trójąta 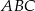 obrano punkt
obrano punkt 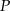 odległy od prostych
odległy od prostych 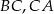 i
i 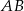 odpowiednio o
odpowiednio o 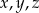 . Wykaż że
. Wykaż że
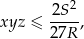
gdzie 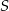 jest polem trójkąta, a
jest polem trójkąta, a 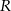 promieniem okręgu opisanego. Dla jakich punktów
promieniem okręgu opisanego. Dla jakich punktów 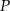 zachodzi równość?
zachodzi równość?
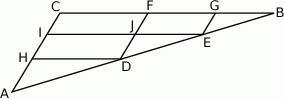
Odcinki 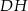 i
i 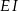 są równoległe do boku
są równoległe do boku 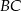 trójkąta
trójkąta 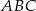 , a odcinki
, a odcinki 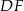 i
i 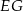 są równoległe do boku
są równoległe do boku 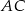 . Uzasadnij, że jeżeli
. Uzasadnij, że jeżeli 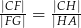 , to
, to 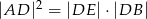 .
.
Trzy okręgi o promieniach 2, 4 i 6 są parami zewnętrznie styczne. Oblicz długość promienia okręgu zawierającego punkty styczności tych okręgów.
Podstawy trapezu mają długości  i
i 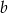 (
(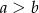 ). Suma miar kątów wewnętrznych przy dłuższej podstawie wynosi
). Suma miar kątów wewnętrznych przy dłuższej podstawie wynosi 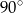 . Oblicz długość odcinka łączącego środki podstaw trapezu.
. Oblicz długość odcinka łączącego środki podstaw trapezu.
Podstawy trapezu 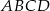 mają długości
mają długości 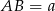 i
i 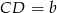 . Na ramionach trapezu wybrano punkty
. Na ramionach trapezu wybrano punkty 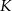 i
i 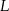 w ten sposób, że odcinek
w ten sposób, że odcinek 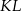 jest równoległy do podstaw oraz
jest równoległy do podstaw oraz 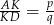 . Oblicz długość odcinka
. Oblicz długość odcinka 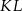 .
.
Odcinek 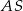 jest środkową trójkąta
jest środkową trójkąta 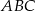 . Udowodnij, że
. Udowodnij, że 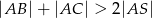 .
.
Okrąg wpisany w trójkąt 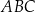 jest styczny do boków
jest styczny do boków 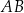 i
i 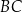 w punktach
w punktach 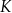 i
i 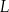 odpowiednio. Na bokach
odpowiednio. Na bokach 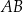 i
i 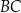 tego trójkąta wybrano punkty
tego trójkąta wybrano punkty 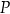 i
i 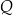 w ten sposób, że odcinek
w ten sposób, że odcinek 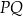 jest styczny do okręgu wpisanego w trójkąt
jest styczny do okręgu wpisanego w trójkąt 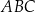 (zobacz rysunek).
(zobacz rysunek).

Wykaż, że jeżeli 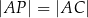 ,
, 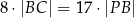 i
i 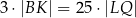 , to trójkąt
, to trójkąt 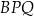 jest rozwartokątny.
jest rozwartokątny.
