Wykaż, że suma odległości dowolnego punktu wewnętrznego trójkąta od jego wierzchołków jest większa od połowy obwodu trójkąta.
/Konkursy/Zadania/Geometria/Planimetria
Uzasadnij, że środki boków dowolnego czworokąta są wierzchołkami równoległoboku. Jaka figurę otrzymamy, łącząc kolejno środki boków: a) rombu, b) prostokąta, c) kwadratu?
Uzasadnij, że środki boków dowolnego czworokąta są wierzchołkami równoległoboku.
Na bokach 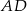 i
i 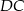 kwadratu
kwadratu 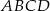 o polu 1 wybrano punkty
o polu 1 wybrano punkty 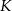 i
i  w ten sposób, że
w ten sposób, że 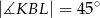 .
.
Oblicz odległość punktu  od prostej
od prostej 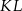 .
.
Dwa okręgi są styczne wewnętrznie w punkcie 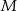 . Cięciwa
. Cięciwa 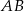 większego okręgu jest styczna do mniejszego okręgu w punkcie
większego okręgu jest styczna do mniejszego okręgu w punkcie 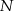 . Oznaczmy przez
. Oznaczmy przez 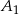 i
i 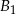 punkty przecięcia prostych
punkty przecięcia prostych 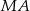 i
i 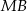 z mniejszym okręgiem. Udowodnić, że
z mniejszym okręgiem. Udowodnić, że
- prosta
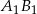 jest równoległa do prostej
jest równoległa do prostej 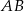 ;
; - prosta
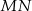 jest dwusieczną kąta
jest dwusieczną kąta 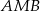 .
.
W trapezie 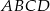 podstawa
podstawa 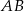 jest 3 razy dłuższa od podstawy
jest 3 razy dłuższa od podstawy 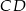 . Przekątne tego trapezu przecinają się w punkcie
. Przekątne tego trapezu przecinają się w punkcie 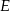 , a proste zawierające ramiona
, a proste zawierające ramiona 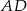 i
i 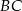 przecinają się w punkcie
przecinają się w punkcie 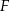 . Oblicz stosunek pola czworokąta
. Oblicz stosunek pola czworokąta 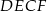 do pola trapezu
do pola trapezu 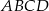 .
.
W trójkącie ostrokątnym 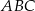 prawdziwa jest równość
prawdziwa jest równość 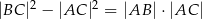 . Wykaż, że kąt
. Wykaż, że kąt 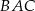 jest dwa razy większy od kąta
jest dwa razy większy od kąta 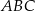 .
.
Przekątne czworokąta wypukłego 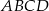 przecinają się w punkcie
przecinają się w punkcie 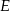 . Wiadomo, że trójkąty
. Wiadomo, że trójkąty 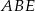 i
i 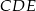 mają równe pola, długość boku
mają równe pola, długość boku 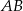 jest równa 4, a przekątna
jest równa 4, a przekątna 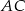 jest zawarta w dwusiecznej kąta
jest zawarta w dwusiecznej kąta 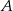 . Oblicz długość boku
. Oblicz długość boku 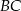 .
.
Wykaż, że jeżeli 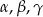 są kątami trójkąta, to
są kątami trójkąta, to
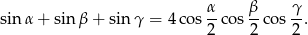
Wyznacz długości boków trójkąta wiedząc, że są one kolejnymi liczbami naturalnymi zaś największy kąt jest dwa razy większy od kąta najmniejszego.
Przez środek 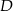 przyprostokątnej
przyprostokątnej 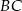 trójkąta prostokątnego
trójkąta prostokątnego 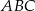 poprowadzono prostą prostopadłą do przeciwprostokątnej
poprowadzono prostą prostopadłą do przeciwprostokątnej 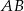 . Prosta ta przecina proste
. Prosta ta przecina proste 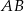 i
i 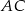 odpowiednio w punktach
odpowiednio w punktach 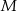 i
i 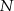 . Wykaż, że
. Wykaż, że 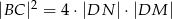 .
.
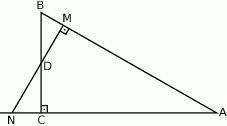
Przez środek  przyprostokątnej
przyprostokątnej  trójkąta prostokątnego
trójkąta prostokątnego  poprowadzono prostą prostopadłą do przeciwprostokątnej
poprowadzono prostą prostopadłą do przeciwprostokątnej 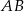 . Prosta ta przecina proste
. Prosta ta przecina proste 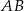 i
i 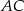 odpowiednio w punktach
odpowiednio w punktach 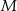 i
i 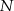 . Wykaż, że skala podobieństwa trójkątów
. Wykaż, że skala podobieństwa trójkątów 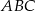 i
i 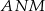 jest równa
jest równa 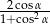 .
.
Trzy koła o promieniu 1 są parami styczne zewnętrznie. Oblicz pole obszaru zawartego między tymi kołami.
Ramiona kąta o mierze 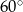 przecięto prostą
przecięto prostą 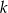 prostopadłą do jednego z ramion kąta i wpisano dwa koła styczne do obu ramion tego kąta i prostej
prostopadłą do jednego z ramion kąta i wpisano dwa koła styczne do obu ramion tego kąta i prostej 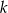 . Oblicz stosunek pól tych kół.
. Oblicz stosunek pól tych kół.
Na okręgu o środku 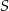 wybrano punkty
wybrano punkty 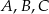 i
i 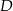 w ten sposób, że prosta
w ten sposób, że prosta 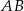 zawiera punkt
zawiera punkt 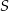 , a proste
, a proste 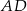 i
i 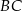 przecinają się w punkcie
przecinają się w punkcie 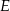 . Punkt
. Punkt 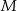 jest punktem wspólnym prostych
jest punktem wspólnym prostych 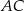 i
i 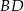 . Wykaż, że proste
. Wykaż, że proste 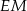 i
i 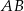 są prostopadłe.
są prostopadłe.
Na bokach  ,
, 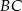 i
i 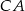 trójkąta
trójkąta 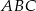 wybrano odpowiednio punkty
wybrano odpowiednio punkty 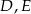 i
i 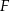 . Wykaż, że okręgi opisane na trójkątach
. Wykaż, że okręgi opisane na trójkątach 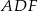 ,
, 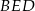 i
i 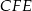 przecinają się w jednym punkcie.
przecinają się w jednym punkcie.
Oblicz długość boku rombu wiedząc, że prosta poprowadzona przez jeden z jego wierzchołków odcina na przedłużeniach dwóch jego boków odcinki o długościach 4 i 9.
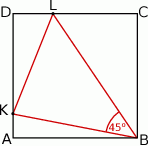
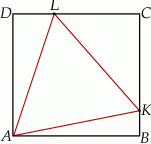
W prostokąt 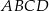 wpisany jest trójkąt równoboczny
wpisany jest trójkąt równoboczny 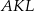 (patrz rysunek). Wierzchołek
(patrz rysunek). Wierzchołek 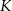 leży na boku
leży na boku 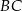 (
(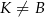 i
i 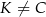 ), wierzchołek
), wierzchołek 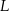 leży na boku
leży na boku 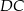 (
(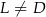 i
i 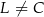 ). Udowodnij, że pole powierzchni trójkąta
). Udowodnij, że pole powierzchni trójkąta 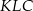 równe jest sumie pól trójkątów
równe jest sumie pól trójkątów 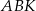 i
i 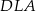 .
.
Na okręgu wybrano takich pięć różnych punktów: 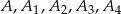 , że
, że
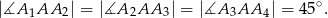
Udowodnij, że punkty  są wierzchołkami kwadratu.
są wierzchołkami kwadratu.
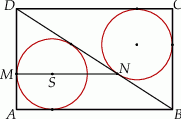
Dany jest prostokąt 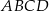 . Okrąg wpisany w trójkąt
. Okrąg wpisany w trójkąt 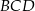 jest styczny do przekątnej
jest styczny do przekątnej 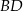 w punkcie
w punkcie 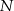 . Okrąg wpisany w trójkąt
. Okrąg wpisany w trójkąt 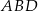 jest styczny do boku
jest styczny do boku 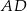 w punkcie
w punkcie 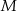 , a środek
, a środek 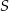 tego okręgu leży na odcinku
tego okręgu leży na odcinku 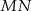 , jak na rysunku.
, jak na rysunku.
Wykaż, że 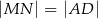 .
.
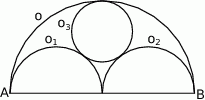
W półkolu  o średnicy
o średnicy 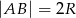 narysowano dwa przystające i zewnętrznie styczne półkola
narysowano dwa przystające i zewnętrznie styczne półkola 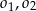 , których środki leżą na odcinku
, których środki leżą na odcinku 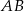 , i które są wewnętrznie styczne do półkola
, i które są wewnętrznie styczne do półkola  . Oblicz promień okręgu
. Oblicz promień okręgu 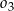 , który jest styczny do
, który jest styczny do 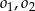 i
i  .
.
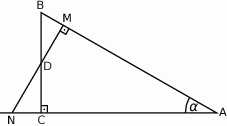
W trójkącie prostokątnym  o kącie prostym w wierzchołku
o kącie prostym w wierzchołku  obrano taki punkt
obrano taki punkt  , że pola trójkątów
, że pola trójkątów 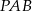 ,
, 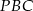 i
i 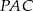 są równe. Oblicz długość odcinka
są równe. Oblicz długość odcinka 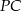 , wiedząc, że
, wiedząc, że 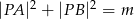 .
.

