Dla jakich wartości parametru 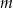 równanie
równanie 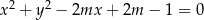 opisuje okrąg?
opisuje okrąg?
- Podaj współrzędne środka i długość promienia okręgu.
- Dla jakich wartości parametru
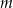 okrąg ten jest styczny do prostej o równaniu
okrąg ten jest styczny do prostej o równaniu 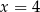 ?
?
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Dla jakich wartości parametru 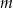 równanie
równanie 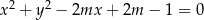 opisuje okrąg?
opisuje okrąg?
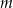 okrąg ten jest styczny do prostej o równaniu
okrąg ten jest styczny do prostej o równaniu 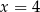 ?
?Punkty 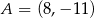 i
i 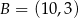 są końcami cięciwy okręgu o środku
są końcami cięciwy okręgu o środku 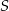 . Napisz równanie prostej prostopadłej do tej tej cięciwy i przechodzącej przez punkt
. Napisz równanie prostej prostopadłej do tej tej cięciwy i przechodzącej przez punkt  .
.
Znajdź równanie okręgu stycznego do prostej 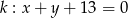 i do prostej
i do prostej 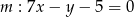 w punkcie
w punkcie 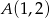 .
.
Środek okręgu przechodzącego przez punkty 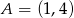 i
i 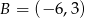 leży na osi
leży na osi 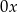 .
.
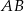 i oddalonej od początku układu współrzędnych o
i oddalonej od początku układu współrzędnych o 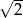 .
.Wyznacz równania prostych stycznych do okręgu o równaniu 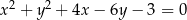 i zarazem prostopadłych do prostej
i zarazem prostopadłych do prostej 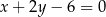 .
.
Wyznacz równania prostych stycznych do okręgu o równaniu 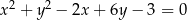 i zarazem prostopadłych do prostej
i zarazem prostopadłych do prostej 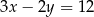 .
.
Wyznacz równania prostych stycznych do okręgu o równaniu 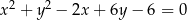 i zarazem prostopadłych do prostej
i zarazem prostopadłych do prostej 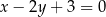 .
.
Znajdź równania stycznych do okręgu 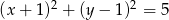 poprowadzonych z punktu
poprowadzonych z punktu 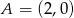 .
.
Znajdź równania stycznych do okręgu 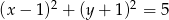 poprowadzonych z punktu
poprowadzonych z punktu 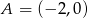 .
.
Wyznacz równania stycznych do okręgu 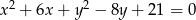 równoległych do osi
równoległych do osi 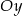 .
.
Wyznacz równania stycznych do okręgu o równaniu 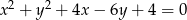 , równoległych do osi rzędnych układu współrzędnych.
, równoległych do osi rzędnych układu współrzędnych.
Wyznacz równania stycznych do okręgu o równaniu 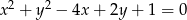 , równoległych do osi odciętych układu współrzędnych.
, równoległych do osi odciętych układu współrzędnych.
Określ wzajemne położenie okręgów 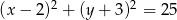 i
i 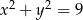 .
.
Określ wzajemne położenie okręgów 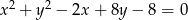 i
i 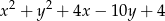 .
.
Określ wzajemne położenie okręgów: 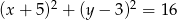 i
i 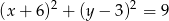 .
.
Napisz równanie okręgu stycznego do osi 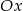 układu współrzędnych o promieniu równym 5 oraz środku należącym do prostej
układu współrzędnych o promieniu równym 5 oraz środku należącym do prostej 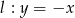 i do drugiej ćwiartki układu współrzędnych. Napisz równanie stycznej do tego okręgu prostopadłej do
i do drugiej ćwiartki układu współrzędnych. Napisz równanie stycznej do tego okręgu prostopadłej do 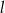 .
.
Dany jest okrąg 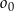 o równaniu
o równaniu 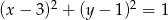 . W pierwszej „ćwiartce” układu współrzędnych istnieją dwa okręgi
. W pierwszej „ćwiartce” układu współrzędnych istnieją dwa okręgi 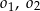 styczne zewnętrznie do okręgu
styczne zewnętrznie do okręgu 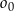 i jednocześnie styczne do obu osi układu współrzędnych. Oblicz odległość środków okręgów
i jednocześnie styczne do obu osi układu współrzędnych. Oblicz odległość środków okręgów 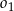 oraz
oraz 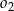 .
.
Dany jest okrąg 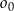 o równaniu
o równaniu 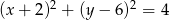 . W drugiej „ćwiartce” układu współrzędnych istnieją dwa okręgi
. W drugiej „ćwiartce” układu współrzędnych istnieją dwa okręgi 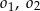 styczne zewnętrznie do okręgu
styczne zewnętrznie do okręgu 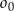 i jednocześnie styczne do obu osi układu współrzędnych. Oblicz odległość środków okręgów
i jednocześnie styczne do obu osi układu współrzędnych. Oblicz odległość środków okręgów 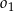 oraz
oraz 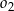 .
.
Dany jest okrąg o równaniu 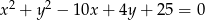 . Napisz równania stycznych do tego okręgu, przechodzących przez początek układu współrzędnych.
. Napisz równania stycznych do tego okręgu, przechodzących przez początek układu współrzędnych.
Wyznacz równania stycznych do okręgu 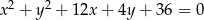 , przechodzących przez początek układu współrzędnych.
, przechodzących przez początek układu współrzędnych.
Okrąg o środku 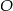 jest wpisany w trójkąt
jest wpisany w trójkąt 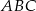 , gdzie
, gdzie 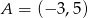 . Wiedząc, że okrąg ten jest styczny do boków
. Wiedząc, że okrąg ten jest styczny do boków 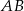 i
i 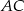 odpowiednio w punktach
odpowiednio w punktach 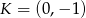 i
i 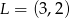 oblicz długość odcinka
oblicz długość odcinka 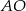 .
.
Wyznacz równanie okręgu przechodzącego przez punkt 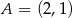 i stycznego do obu osi układu współrzędnych. Rozważ wszystkie przypadki.
i stycznego do obu osi układu współrzędnych. Rozważ wszystkie przypadki.
Prosta 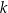 przecina okrąg o środku
przecina okrąg o środku 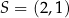 w punktach
w punktach 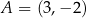 i
i 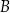 , przy czym
, przy czym 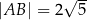 . Wyznacz równanie prostej
. Wyznacz równanie prostej 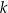 .
.
Napisz równanie okręgu o środku 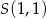 , który na prostej o równaniu
, który na prostej o równaniu 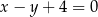 odcina cięciwę
odcina cięciwę 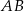 długości
długości 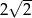 . Wykonaj rysunek.
. Wykonaj rysunek.
Prosta o równaniu 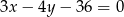 przecina okrąg o środku
przecina okrąg o środku 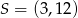 w punktach
w punktach 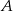 i
i 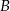 . Długość odcinka
. Długość odcinka 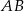 jest równa 40. Wyznacz równanie tego okręgu.
jest równa 40. Wyznacz równanie tego okręgu.
Wyznacz środek okręgu przechodzącego przez punkty 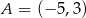 i
i 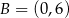 , którego środek leży na prostej o równaniu
, którego środek leży na prostej o równaniu 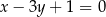 .
.
Wykaż, że styczne do okręgu 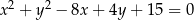 poprowadzone przez punkt
poprowadzone przez punkt 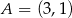 są prostopadłe.
są prostopadłe.
Podaj współrzędne środka i długość promienia okręgu o równaniu: 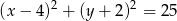 .
.
Podaj współrzędne środka i długość promienia okręgu o równaniu: 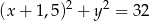 .
.
Podaj współrzędne środka i długość promienia okręgu o równaniu: 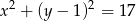 .
.
Podaj współrzędne środka i długość promienia okręgu o równaniu: 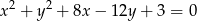 .
.
Wyznacz współrzędne środka i promień okręgu o równaniu 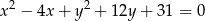 .
.
Podaj współrzędne środka i długość promienia okręgu o równaniu 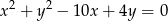 .
.
Okrąg 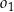 o równaniu
o równaniu 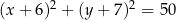 oraz okrąg
oraz okrąg 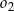 o środku
o środku 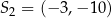 są wewnętrznie styczne, przy czym okrąg
są wewnętrznie styczne, przy czym okrąg 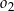 zawiera się w kole opisanym nierównością
zawiera się w kole opisanym nierównością 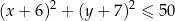 . Napisz równanie wspólnej stycznej do obu okręgów.
. Napisz równanie wspólnej stycznej do obu okręgów.
Napisz równanie okręgu o środku w punkcie 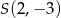 , stycznego do osi
, stycznego do osi 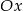 .
.
Środek okręgu, stycznego do osi 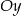 i do prostej o równaniu
i do prostej o równaniu 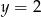 , ma obie współrzędne ujemne. Promień okręgu ma długość 5. Wyznacz równanie tego okręgu.
, ma obie współrzędne ujemne. Promień okręgu ma długość 5. Wyznacz równanie tego okręgu.
Napisz równanie okręgu o promieniu 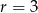 , stycznego do obu osi układu.
, stycznego do obu osi układu.
