Styczne do okręgu o równaniu 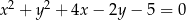 , które są równoległe do prostej o równaniu
, które są równoległe do prostej o równaniu 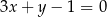 , przecinają prostą
, przecinają prostą 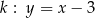 w punktach
w punktach 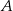 i
i 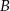 . Oblicz pole trójkąta
. Oblicz pole trójkąta 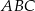 , jeśli
, jeśli 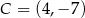 .
.
/Szkoła średnia/Geometria/Geometria analityczna/Okrąg
Prosta o równaniu 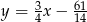 jest styczna od okręgu o środku
jest styczna od okręgu o środku 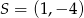 . Wyznacz promień tego okręgu.
. Wyznacz promień tego okręgu.
Prosta o równaniu 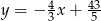 jest styczna od okręgu o środku
jest styczna od okręgu o środku 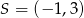 . Wyznacz promień tego okręgu.
. Wyznacz promień tego okręgu.
Okrąg o równaniu 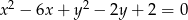 i prosta
i prosta 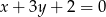 przecinają się w punktach
przecinają się w punktach 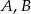 . Wyznacz długość cięciwy
. Wyznacz długość cięciwy 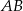 tego okręgu.
tego okręgu.
Dla jakiej wartości 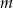 wykres funkcji
wykres funkcji 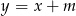 ma co najmniej jeden punkt wspólny z okręgiem o promieniu
ma co najmniej jeden punkt wspólny z okręgiem o promieniu  , którego środkiem jest początek układu współrzędnych?
, którego środkiem jest początek układu współrzędnych?
Okrąg o środku 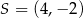 przechodzi przez punkt
przechodzi przez punkt 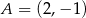 . Napisz równanie stycznej do tego okręgu przechodzącej przez punkt
. Napisz równanie stycznej do tego okręgu przechodzącej przez punkt 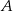 .
.
Okrąg o równaniu 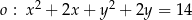 jest styczny do prostych
jest styczny do prostych 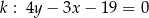 i
i 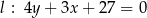 w punktach
w punktach  i
i 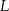 odpowiednio. Wyznacz równania wszystkich okręgów, które są jednocześnie styczne do okręgu
odpowiednio. Wyznacz równania wszystkich okręgów, które są jednocześnie styczne do okręgu  , prostych
, prostych 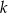 i
i 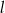 , oraz nie przechodzą przez punkty
, oraz nie przechodzą przez punkty 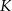 i
i 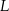 .
.
Określ wzajemne położenie okręgów: 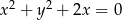 i
i 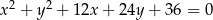 .
.
Końce cięciwy 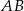 okręgu o równaniu
okręgu o równaniu 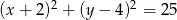 leżą na prostej
leżą na prostej 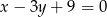 . Oblicz sinus kąta wypukłego
. Oblicz sinus kąta wypukłego 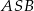 , gdzie
, gdzie 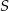 jest środkiem danego okręgu.
jest środkiem danego okręgu.
Wyznacz środek okręgu wpisanego w trójkąt, którego boki zwierają się w prostych o równaniach 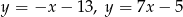 oraz
oraz 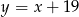 .
.
Oblicz miarę kąta między stycznymi do okręgu  poprowadzonymi przez punkt
poprowadzonymi przez punkt 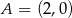 .
.
Oblicz miarę kąta między stycznymi do okręgu 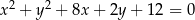 poprowadzonymi przez punkt
poprowadzonymi przez punkt 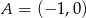 .
.
Znajdź równanie obrazu krzywej 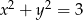 w przesunięciu o wektor
w przesunięciu o wektor ![u = [− 4 ,2 ]](https://img.zadania.info/zad/4910174/HzadT1x.gif) .
.
Oblicz odległość środka okręgu 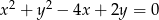 od prostej
od prostej 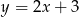 .
.
Dane są dwa okręgi o równaniach 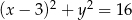 i
i 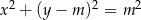 ,
, 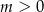 . Wyznacz wszystkie wartości parametru
. Wyznacz wszystkie wartości parametru 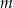 , dla których te okręgi mają jeden punkt wspólny.
, dla których te okręgi mają jeden punkt wspólny.
Dane są dwa okręgi o równaniach 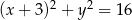 i
i 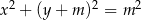 ,
, 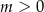 . Wyznacz wszystkie wartości parametru
. Wyznacz wszystkie wartości parametru 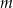 , dla których te okręgi mają jeden punkt wspólny.
, dla których te okręgi mają jeden punkt wspólny.
Wyznacz współrzędne punktów wspólnych prostej 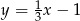 i okręgu
i okręgu 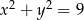 .
.
Wyznacz punkty wspólne okręgu 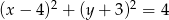 oraz prostej
oraz prostej 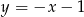 .
.
Napisz równanie okręgu, którego środek znajduje się na prostej 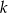 , przechodzącego przez punkty
, przechodzącego przez punkty 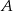 i
i 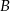 , jeśli
, jeśli 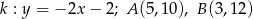 .
.
Okrąg przechodzi przez punkty 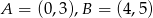 , a jego środek należy do prostej o równaniu
, a jego środek należy do prostej o równaniu 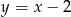 . Wyznacz równanie tego okręgu.
. Wyznacz równanie tego okręgu.
Napisz równanie okręgu, którego środek znajduje się na prostej 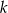 , przechodzącego przez punkty
, przechodzącego przez punkty 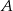 i
i 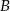 , jeśli
, jeśli 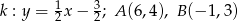 .
.
Oblicz długość cięciwy, którą wycina z prostej 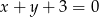 okrąg o środku w punkcie
okrąg o środku w punkcie 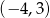 i promieniu 10.
i promieniu 10.
Oblicz długość cięciwy, którą wycina z prostej 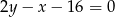 okrąg o środku w punkcie
okrąg o środku w punkcie 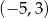 i promieniu 5.
i promieniu 5.
Przez początek układu współrzędnych poprowadzono prostą przecinającą okrąg 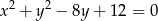 w dwóch punktach
w dwóch punktach 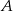 i
i 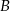 . Uzasadnij, że liczba
. Uzasadnij, że liczba  nie zależy od wyboru prostej i oblicz wartość tego iloczynu.
nie zależy od wyboru prostej i oblicz wartość tego iloczynu.
Napisz równanie okręgu przechodzącego przez punkt 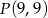 i stycznego do osi
i stycznego do osi  w punkcie
w punkcie 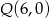 .
.
Do okręgu należy punkt 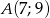 , oraz jest on styczny do osi
, oraz jest on styczny do osi 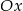 w punkcie
w punkcie 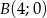 . Podaj równanie tego okręgu.
. Podaj równanie tego okręgu.
Punkt 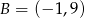 należy do okręgu stycznego do osi
należy do okręgu stycznego do osi 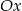 w punkcie
w punkcie 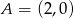 . Wyznacz równanie tego okręgu.
. Wyznacz równanie tego okręgu.
Do okręgu należy punkt 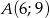 , oraz jest on styczny do osi
, oraz jest on styczny do osi 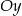 w punkcie
w punkcie 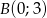 . Podaj równanie tego okręgu.
. Podaj równanie tego okręgu.
Napisz równanie okręgu przechodzącego przez punkt 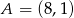 i stycznego do osi
i stycznego do osi 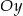 w punkcie
w punkcie 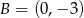 .
.
Punkty 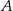 i
i 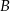 są punktami wspólnymi prostej o równaniu
są punktami wspólnymi prostej o równaniu 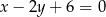 oraz okręgu o środku
oraz okręgu o środku 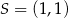 . Długość odcinka
. Długość odcinka 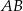 jest równa
jest równa 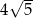 . Wyznacz współrzędne punktów
. Wyznacz współrzędne punktów 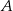 i
i 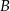 .
.
Punkt 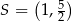 leży wewnątrz figury
leży wewnątrz figury 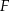 opisanej układem nierówności
opisanej układem nierówności
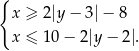
Wyznacz równanie największego okręgu o środku 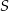 , który jest zawarty wewnątrz figury
, który jest zawarty wewnątrz figury 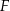 .
.

