Punkt 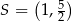 leży wewnątrz figury
leży wewnątrz figury 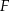 opisanej układem nierówności
opisanej układem nierówności
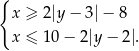
Wyznacz równanie największego okręgu o środku 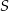 , który jest zawarty wewnątrz figury
, który jest zawarty wewnątrz figury 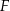 .
.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Punkt 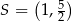 leży wewnątrz figury
leży wewnątrz figury 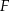 opisanej układem nierówności
opisanej układem nierówności
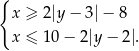
Wyznacz równanie największego okręgu o środku 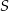 , który jest zawarty wewnątrz figury
, który jest zawarty wewnątrz figury 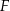 .
.
Wyznacz równanie okręgu o środku 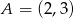 , stycznego do prostej o równaniu
, stycznego do prostej o równaniu 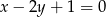 .
.
Wyznacz równanie okręgu o środku 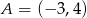 , stycznego do prostej o równaniu
, stycznego do prostej o równaniu 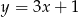 .
.
Wyznacz równanie okręgu o środku 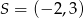 stycznego do prostej
stycznego do prostej 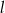 o równaniu
o równaniu 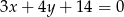 .
.
Wyznacz równanie prostej prostopadłej do wektora ![→ u = [0,− 3]](https://img.zadania.info/zad/6101909/HzadT0x.gif) i stycznej do okręgu
i stycznej do okręgu 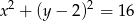 .
.
Wyznacz równania prostych stycznych do okręgu o równaniu 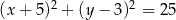 równoległych do prostej o równaniu
równoległych do prostej o równaniu 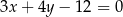 .
.
Wyznacz równania prostych stycznych do okręgu o równaniu 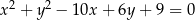 równoległych do prostej o równaniu
równoległych do prostej o równaniu 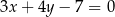 .
.
Uzasadnij, że koło o środku 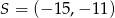 i promieniu
i promieniu 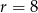 jest w całości zawarte w trójkącie o wierzchołkach
jest w całości zawarte w trójkącie o wierzchołkach 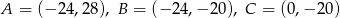 .
.
Znajdź równanie okręgu o środku w punkcie 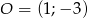 , wiedząc, że okrąg jest styczny do prostej
, wiedząc, że okrąg jest styczny do prostej 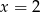 .
.
Środki okręgów 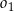 i
i 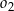 znajdują się po różnych stronach prostej
znajdują się po różnych stronach prostej 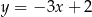 , która zawiera punkty wspólne tych okręgów. Wiedząc, że promień okręgu
, która zawiera punkty wspólne tych okręgów. Wiedząc, że promień okręgu 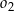 jest równy
jest równy 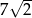 oraz, że okrąg
oraz, że okrąg 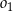 ma równanie
ma równanie 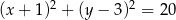 , wyznacz równanie okręgu
, wyznacz równanie okręgu 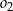 .
.
Dane są okrąg 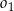 o równaniu
o równaniu 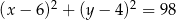 oraz okrąg
oraz okrąg 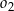 o promieniu
o promieniu 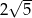 . Środki okręgów
. Środki okręgów 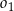 i
i 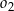 leżą po różnych stronach prostej
leżą po różnych stronach prostej 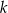 o równaniu
o równaniu 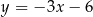 , a punkty wspólne obu okręgów leżą na prostej
, a punkty wspólne obu okręgów leżą na prostej 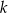 . Wyznacz równanie okręgu
. Wyznacz równanie okręgu 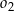 .
.
Wyznacz wszystkie wartości parametru 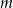 , dla których prosta o równaniu
, dla których prosta o równaniu 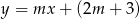 ma dokładnie dwa punkty wspólne z okręgiem o środku w punkcie
ma dokładnie dwa punkty wspólne z okręgiem o środku w punkcie 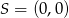 i promieniu
i promieniu 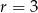 .
.
Prosta 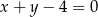 przecina oś
przecina oś 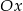 w punkcie
w punkcie 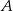 i oś
i oś 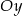 w punkcie
w punkcie 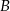 . Punkt
. Punkt 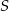 jest środkiem odcinka
jest środkiem odcinka 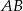 . Znajdź równanie okręgu o środku w punkcie
. Znajdź równanie okręgu o środku w punkcie 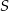 i promieniu
i promieniu 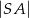 .
.
Dany jest okrąg o środku w punkcie 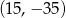 i promieniu 16. Sprawdź czy okrąg ten jest styczny do
i promieniu 16. Sprawdź czy okrąg ten jest styczny do
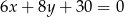 ,
, 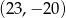 i promieniu 2?
i promieniu 2?Uzasadnij swoją odpowiedź.
Napisz równanie okręgu o środku 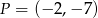 , którego punkty wspólne z okręgiem o równaniu
, którego punkty wspólne z okręgiem o równaniu 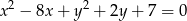 są końcami odcinka o długości
są końcami odcinka o długości 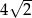 .
.
Okrąg o środku w punkcie 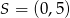 ma promień długości 1 i jest styczny do okręgu o środku
ma promień długości 1 i jest styczny do okręgu o środku 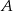 i promieniu długości 10. Punkt
i promieniu długości 10. Punkt 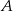 leży na osi
leży na osi 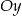 . Jakie ma współrzędne?
. Jakie ma współrzędne?
Znajdź równanie okręgu przechodzącego przez punkt 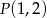 i stycznego jednocześnie do prostych
i stycznego jednocześnie do prostych 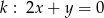 i
i 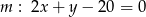 .
.
Napisz równanie okręgu stycznego do osi 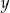 w punkcie
w punkcie 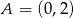 i przechodzącego przez punkt
i przechodzącego przez punkt 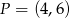 . Wyznacz na okręgu takie punkty
. Wyznacz na okręgu takie punkty 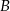 i
i 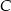 , aby trójkąt
, aby trójkąt 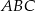 był równoboczny.
był równoboczny.
Wyznacz równanie okręgu stycznego wewnętrznie do okręgu o równaniu 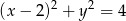 i do prostej
i do prostej 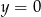 , którego środek ma współrzędne różnych znaków i leży na wykresie funkcji
, którego środek ma współrzędne różnych znaków i leży na wykresie funkcji 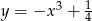 .
.
Ile punktów wspólnych ma okrąg o równaniu 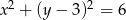 z prostą o równaniu
z prostą o równaniu 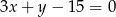 ?
?
Okrąg  ma środek
ma środek 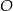 i jest styczny prostej
i jest styczny prostej 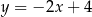 w punkcie
w punkcie 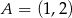 . Wyznacz równanie okręgu
. Wyznacz równanie okręgu  , jeżeli
, jeżeli ![−→ OA = [2,1]](https://img.zadania.info/zad/7820974/HzadT5x.gif) .
.
Znajdź równania prostych stycznych do dwóch okręgów: 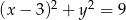 i
i 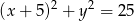 .
.
Okrąg o równaniu 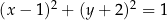 przecina jedną z gałęzi hiperboli o równaniu
przecina jedną z gałęzi hiperboli o równaniu 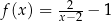 , gdzie
, gdzie 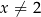 , w punktach
, w punktach 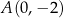 i
i 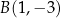 .
.
Narysuj obie krzywe we wspólnym układzie współrzędnych.
Na drugiej gałęzi hiperboli wyznacz współrzędne takiego punktu 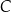 , który jest równo odległy od punktów
, który jest równo odległy od punktów 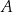 i
i 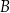 .
.
Dane są punkty 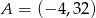 i
i 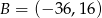 . Wykaż, że koło o średnicy
. Wykaż, że koło o średnicy 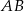 jest zawarte w II ćwiartce prostokątnego układu współrzędnych.
jest zawarte w II ćwiartce prostokątnego układu współrzędnych.
