Okrąg jest styczny do osi układu współrzędnych w punktach 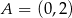 i
i 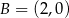 oraz jest styczny do prostej
oraz jest styczny do prostej 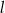 w punkcie
w punkcie 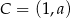 , gdzie
, gdzie 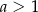 . Wyznacz równanie prostej
. Wyznacz równanie prostej 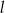 .
.
/Szkoła średnia/Geometria/Geometria analityczna/Okrąg
Okrąg jest styczny do osi układu współrzędnych w punktach 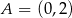 i
i 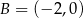 oraz jest styczny do prostej
oraz jest styczny do prostej 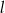 w punkcie
w punkcie 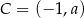 , gdzie
, gdzie 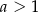 . Wyznacz równanie prostej
. Wyznacz równanie prostej 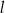 .
.
Dany jest okrąg o równaniu 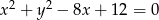 .
.
- Wyznacz równania stycznych do okręgu przechodzących przez początek układu współrzędnych.
- Oblicz pole figury ograniczonej stycznymi i łukiem okręgu wyznaczonym przez punkty styczności.
Z punktu 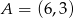 poprowadzono styczne do okręgu
poprowadzono styczne do okręgu 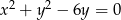 .
.
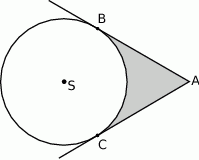
- Wyznacz równania tych stycznych.
- Oblicz odległość punktów styczności.
- Oblicz pole figury zaznaczonej na rysunku.
Dany jest okrąg o równaniu 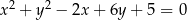 .
.
- Napisz równania stycznych do danego okręgu, prostopadłych do prostej o równaniu
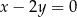 .
. - Oblicz pole trójkąta
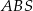 , gdzie
, gdzie 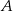 i
i 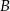 są punktami przecięcia się stycznych z prostą o równaniu
są punktami przecięcia się stycznych z prostą o równaniu 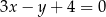 , zaś
, zaś 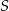 jest środkiem danego okręgu.
jest środkiem danego okręgu.
W układzie współrzędnych dany jest okrąg  opisany równaniem
opisany równaniem 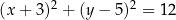 . Sprawdź, czy prosta o równaniu
. Sprawdź, czy prosta o równaniu 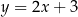 jest styczna do okręgu
jest styczna do okręgu  .
.
Wyznacz równanie okręgu stycznego do osi 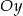 , którego środkiem jest punkt
, którego środkiem jest punkt 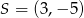 .
.
Okrąg o środku w punkcie 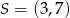 jest styczny do prostej o równaniu
jest styczny do prostej o równaniu 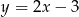 . Oblicz współrzędne punktu styczności.
. Oblicz współrzędne punktu styczności.
Okrąg o środku w punkcie 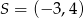 jest styczny do prostej o równaniu
jest styczny do prostej o równaniu 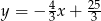 . Oblicz współrzędne punktu styczności.
. Oblicz współrzędne punktu styczności.
Okrąg o środku w punkcie 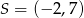 jest styczny do prostej o równaniu
jest styczny do prostej o równaniu 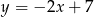 . Oblicz współrzędne punktu styczności.
. Oblicz współrzędne punktu styczności.
Okrąg o środku w punkcie 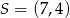 jest styczny do prostej o równaniu
jest styczny do prostej o równaniu 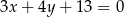 . Oblicz promień tego okręgu oraz współrzędne punktu styczności.
. Oblicz promień tego okręgu oraz współrzędne punktu styczności.
Napisz równanie okręgu, który jest styczny do prostej 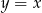 w punkcie
w punkcie 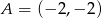 , oraz który odcina z prostej
, oraz który odcina z prostej 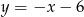 cięciwę o długości 8.
cięciwę o długości 8.
Zapisz równanie okręgu o środku 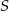 i promieniu
i promieniu  , jeśli
, jeśli 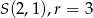 .
.
Zapisz równanie okręgu o środku 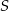 i promieniu
i promieniu  , jeśli
, jeśli 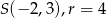 .
.
Dany jest okrąg o równaniu 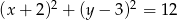 oraz punkt
oraz punkt 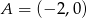 . Napisz równanie symetralnej odcinka, którego końcami są dany punkt
. Napisz równanie symetralnej odcinka, którego końcami są dany punkt 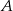 i środek
i środek 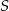 danego okręgu.
danego okręgu.
Z punktu 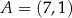 poprowadzono styczne do okręgu
poprowadzono styczne do okręgu 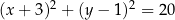 . Oblicz pole trójkąta
. Oblicz pole trójkąta 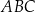 , gdzie
, gdzie 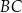 jest odcinkiem łączącym punkty styczności.
jest odcinkiem łączącym punkty styczności.
Z punktu 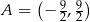 poprowadzono styczne do okręgu
poprowadzono styczne do okręgu 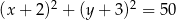 . Oblicz pole trójkąta
. Oblicz pole trójkąta 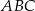 , gdzie
, gdzie 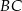 jest odcinkiem łączącym punkty styczności.
jest odcinkiem łączącym punkty styczności.
Wyznacz wszystkie wartości parametru 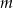 , dla których okrąg o równaniu
, dla których okrąg o równaniu 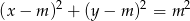 jest styczny do prostej
jest styczny do prostej 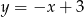 .
.
Z punktu 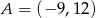 poprowadzono styczne do okręgu o równaniu
poprowadzono styczne do okręgu o równaniu 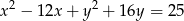 . Oblicz długość odcinka łączącego punkty styczności.
. Oblicz długość odcinka łączącego punkty styczności.
Z punktu 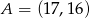 poprowadzono styczne do okręgu o równaniu
poprowadzono styczne do okręgu o równaniu 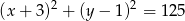 . Oblicz długość odcinka łączącego punkty styczności.
. Oblicz długość odcinka łączącego punkty styczności.
W układzie współrzędnych punkty 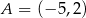 i
i 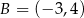 są końcami cięciwy okręgu
są końcami cięciwy okręgu  . Średnica
. Średnica 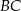 tego okręgu jest zwarta w prostej o równaniu
tego okręgu jest zwarta w prostej o równaniu 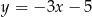 . Wyznacz współrzędne punktu
. Wyznacz współrzędne punktu 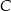 .
.
Wyznacz równanie okręgu o promieniu  , który przechodzi przez punkty wspólne okręgów o równaniach
, który przechodzi przez punkty wspólne okręgów o równaniach 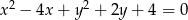 i
i 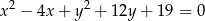 .
.
Sprawdź, czy odległość środka okręgu 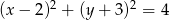 od prostej
od prostej 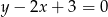 jest równa promieniowi okręgu.
jest równa promieniowi okręgu.
Wykaż, że prosta 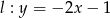 jest styczna do okręgu
jest styczna do okręgu 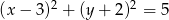 .
.
Sprawdź, czy prosta 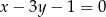 jest styczna do okręgu
jest styczna do okręgu 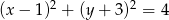 .
.
Wyznacz równanie prostych przechodzących przez początek układu współrzędnych i stycznych do okręgu o środku w punkcie 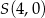 i promieniu
i promieniu 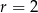 .
.
Dany jest odcinek o końcach 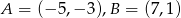 .
.
- Wyznacz równanie symetralnej tego odcinka.
- Wyznacz równanie okręgu o średnicy
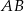 .
.
Dany jest odcinek o końcach 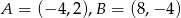 .
.
- Wyznacz równanie okręgu o średnicy
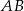 .
. - Wyznacz równanie średnicy prostopadłej do średnicy
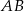 .
.
Wyznacz równanie prostej przechodzącej przez początek układu współrzędnych i przez środek okręgu o równaniu 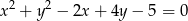 .
.
Wyznacz równanie prostej przechodzącej przez początek układu współrzędnych i przez środek okręgu o równaniu 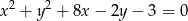 .
.
Wyznacz równanie prostej przechodzącej przez początek układu współrzędnych i przez środek okręgu o równaniu 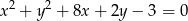 .
.
Ile punktów wspólnych ma prosta 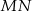 z okręgiem
z okręgiem 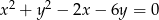 jeśli
jeśli 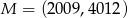 oraz
oraz 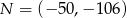 .
.

