Pole trapezu jest równe 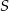 , a stosunek długości jego podstaw wynosi
, a stosunek długości jego podstaw wynosi 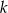 . Przekątne dzielą trapez na cztery trójkąty. Oblicz pole każdego z tych trójkątów.
. Przekątne dzielą trapez na cztery trójkąty. Oblicz pole każdego z tych trójkątów.
/Szkoła średnia/Geometria/Planimetria/Czworokąt/Trapez
W trapezie 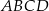 mamy
mamy 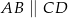 oraz
oraz 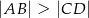 . Punkt
. Punkt 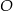 jest środkiem ramienia
jest środkiem ramienia 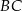 , a punkt
, a punkt 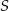 jest punktem wspólnym prostych
jest punktem wspólnym prostych 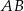
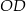 . Udowodnij, że pole trójkąta
. Udowodnij, że pole trójkąta 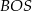 jest równe polu trójkąta
jest równe polu trójkąta 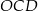 .
.
Dany jest trapez równoramienny 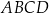 , w którym podstawa
, w którym podstawa 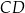 ma długość 6, ramię
ma długość 6, ramię 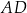 ma długość 4, a kąty
ma długość 4, a kąty 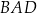 oraz
oraz  mają miarę
mają miarę 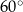 (zobacz rysunek).
(zobacz rysunek).
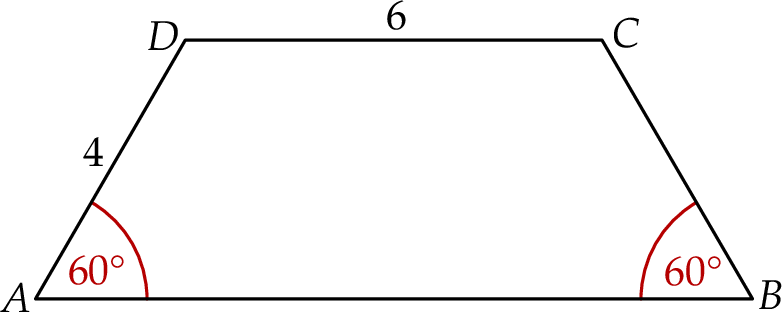
Oblicz pole tego trapezu.
Dany jest trapez równoramienny  , w którym podstawa
, w którym podstawa 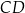 ma długość 8, ramię
ma długość 8, ramię 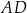 ma długość 6, a kąty
ma długość 6, a kąty 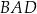 oraz
oraz 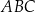 mają miarę
mają miarę 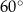 (zobacz rysunek).
(zobacz rysunek).
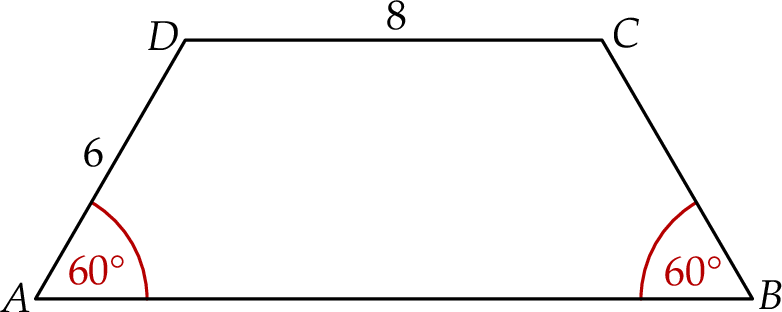
Oblicz pole tego trapezu.
Trapez 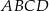 jest wpisany w okrąg, przekątna
jest wpisany w okrąg, przekątna 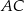 jest zawarta w dwusiecznej kąta
jest zawarta w dwusiecznej kąta 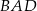 , a długość podstawy
, a długość podstawy 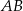 jest dwa razy większa niż długość podstawy
jest dwa razy większa niż długość podstawy 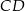 . Oblicz pole trapezu i obwód wiedząc że jego wysokość jest równa
. Oblicz pole trapezu i obwód wiedząc że jego wysokość jest równa 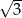 .
.
Dany jest trapez 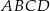 o podstawach
o podstawach 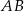 i
i 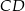 , w którym
, w którym 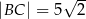 . Okrąg opisany na trójkącie
. Okrąg opisany na trójkącie 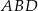 przecina prostą
przecina prostą 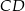 w takim punkcie
w takim punkcie 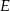 , że
, że 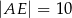 i
i 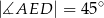 . Oblicz długość podstawy
. Oblicz długość podstawy 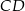 trapezu
trapezu 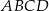 .
.
Wykaż, że w trapezie prostokątnym różnica kwadratów długości przekątnych równa jest różnicy kwadratów długości podstaw.
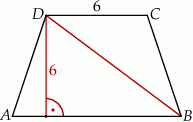
W trapezie równoramiennym 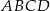 krótsza podstawa
krótsza podstawa 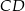 ma długość równą 6 i jest równa wysokości trapezu. Długość dłuższej podstawy
ma długość równą 6 i jest równa wysokości trapezu. Długość dłuższej podstawy 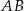 jest równa długości przekątnej trapezu. Oblicz pole tego trapezu.
jest równa długości przekątnej trapezu. Oblicz pole tego trapezu.
Podstawy trapezu prostokątnego mają długości 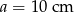 i
i 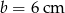 , zaś bok prostopadły do podstaw ma długość
, zaś bok prostopadły do podstaw ma długość 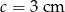 .
.
- Oblicz odległość punktu przecięcia się przekątnych tego trapezu od podstawy długości
 i ramienia długości
i ramienia długości  .
. - Czy w trapez można wpisać okrąg? Odpowiedź uzasadnij.
Trapez równoramienny jest opisany na okręgu. Obwód trapezu wynosi 16cm, a przekątna ma długość 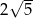 . Oblicz długości boków tego trapezu.
. Oblicz długości boków tego trapezu.
Oblicz pole trapezu  , którego podstawy mają długości
, którego podstawy mają długości 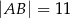 i
i 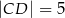 , a ramiona mają długości
, a ramiona mają długości 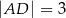 i
i 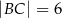 .
.
W trapezie równoramiennym o podstawach długości 20 i 40, oraz kącie ostrym o mierze 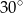 połączono środki wszystkich boków. Oblicz pole otrzymanego czworokąta.
połączono środki wszystkich boków. Oblicz pole otrzymanego czworokąta.
W trapezie  dane są długości podstaw:
dane są długości podstaw: 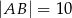 ,
, 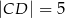 i ramion:
i ramion: 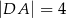 ,
, 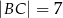 . Oblicz długość przekątnej
. Oblicz długość przekątnej 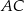 tego trapezu.
tego trapezu.
W trapezie 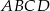 o podstawach
o podstawach 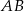 i
i 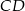 punkt
punkt 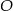 jest punktem wspólnym przekątnych. Oblicz pole trapezu wiedząc, że pole trójkąta
jest punktem wspólnym przekątnych. Oblicz pole trapezu wiedząc, że pole trójkąta 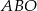 jest równe 5, a pole trójkąta
jest równe 5, a pole trójkąta 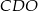 jest równe 4.
jest równe 4.
W trapezie 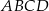 ramię
ramię 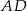 i podstawa
i podstawa 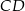 mają długość 4, a ramię
mają długość 4, a ramię 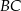 i przekątna
i przekątna 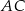 mają długość 6. Oblicz długość podstawy
mają długość 6. Oblicz długość podstawy 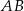 .
.
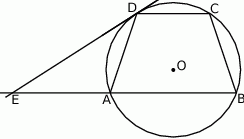
W okrąg wpisano trapez równoramienny 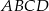 , którego podstawy mają długości:
, którego podstawy mają długości: 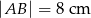 ,
, 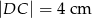 . Styczna do okręgu w punkcie
. Styczna do okręgu w punkcie 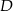 przecina prostą
przecina prostą 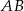 w punkcie
w punkcie 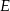 (rys). Wiedząc, że
(rys). Wiedząc, że 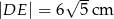 oblicz promień okręgu opisanego na trapezie
oblicz promień okręgu opisanego na trapezie 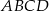 .
.
Podstawy trapezu równoramiennego mają długości  i
i 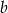 , a jego przekątna ma długość
, a jego przekątna ma długość 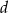 . Wyznacz cosinus kąta między przekątnymi tego trapezu.
. Wyznacz cosinus kąta między przekątnymi tego trapezu.
Podstawy trapezu prostokątnego  mają długości:
mają długości: 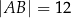 oraz
oraz 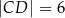 . Wysokość
. Wysokość 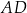 tego trapezu ma długość 24. Na odcinku
tego trapezu ma długość 24. Na odcinku 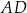 leży punkt
leży punkt 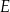 taki, że
taki, że 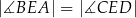 (zobacz rysunek).
(zobacz rysunek).
Oblicz długość odcinka  .
.
Dany jest trapez 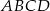 o podstawach
o podstawach 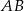 i
i 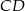 . Przekątne tego trapezu przecinają się w punkcie
. Przekątne tego trapezu przecinają się w punkcie 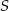 . Wykaż, że
. Wykaż, że 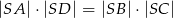 .
.
W trapezie 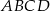 o podstawach
o podstawach 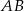 i
i 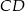 punkt
punkt 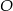 jest punktem wspólnym przekątnych. Oblicz pole trapezu wiedząc, że pole trójkąta
jest punktem wspólnym przekątnych. Oblicz pole trapezu wiedząc, że pole trójkąta 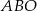 jest równe
jest równe 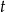 , a pole trójkąta
, a pole trójkąta 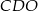 jest równe
jest równe  .
.
W okrąg o średnicy 26 wpisano trapez równoramienny w ten sposób, że suma kwadratów długości jego podstaw jest równa 914, a sinus kąta ostrego wynosi 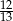 . Oblicz pole tego trapezu.
. Oblicz pole tego trapezu.

