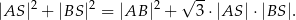Punkt 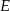 jest punktem wspólnym dwusiecznych kątów
jest punktem wspólnym dwusiecznych kątów 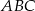 i
i 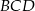 trapezu
trapezu 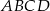 o podstawach
o podstawach 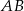 i
i 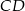 . Punkt
. Punkt 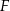 jest środkiem odcinka
jest środkiem odcinka 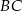 (zobacz rysunek).
(zobacz rysunek).
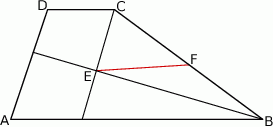
Wykaż, że 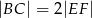 .
.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Punkt 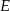 jest punktem wspólnym dwusiecznych kątów
jest punktem wspólnym dwusiecznych kątów 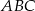 i
i 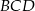 trapezu
trapezu 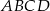 o podstawach
o podstawach 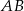 i
i 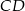 . Punkt
. Punkt 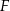 jest środkiem odcinka
jest środkiem odcinka 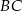 (zobacz rysunek).
(zobacz rysunek).

Wykaż, że 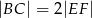 .
.
Na okręgu o promieniu 8 cm opisano trapez. Kąty, które tworzą ramiona z dłuższą podstawą mają miarę 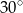 . Oblicz pole tego trapezu.
. Oblicz pole tego trapezu.
W trapezie prostokątnym 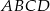 na rysunku poniżej dane są:
na rysunku poniżej dane są: 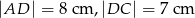 oraz
oraz 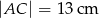 .
.
Oblicz:
 ,
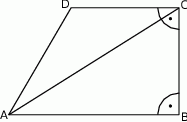
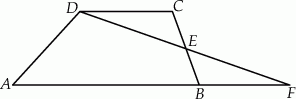
, Na rysunku przedstawiono trapez 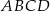 i trójkąt
i trójkąt 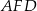 . Punkt
. Punkt 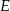 leży w połowie odcinka
leży w połowie odcinka 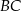 . Uzasadnij, że pole trapezu
. Uzasadnij, że pole trapezu 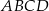 i pole trójkąta
i pole trójkąta 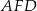 są równe.
są równe.
Oblicz pole trapezu, którego podstawy mają długości 2 i 3, a przekątne długości 3 i 4.
W trapezie prostokątnym 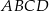 krótsze ramię
krótsze ramię 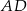 i krótsza podstawa
i krótsza podstawa 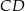 mają tę samą długość oraz
mają tę samą długość oraz 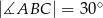 . Na podstawie
. Na podstawie 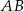 wybrano punkt
wybrano punkt 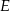 tak, że
tak, że 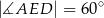 oraz
oraz 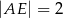 (zobacz rysunek). Oblicz długość odcinka
(zobacz rysunek). Oblicz długość odcinka 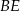 .
.
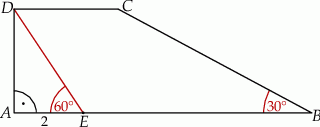
Wiedząc, że 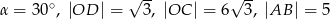 oraz
oraz 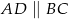 , oblicz pole i obwód trapezu
, oblicz pole i obwód trapezu  przedstawionego na rysunku.
przedstawionego na rysunku.
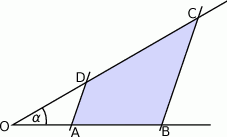
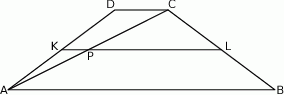
W trapezie równoramiennym 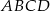 punkty
punkty 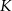 i
i 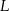 są odpowiednio środkami ramion
są odpowiednio środkami ramion 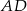 i
i 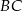 . Przekątna
. Przekątna 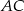 przecina odcinek
przecina odcinek 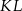 w punkcie
w punkcie 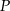 . Wiedząc, że
. Wiedząc, że 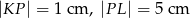 oraz wysokość trapezu jest równa 3 cm, oblicz długość boków trapezu.
oraz wysokość trapezu jest równa 3 cm, oblicz długość boków trapezu.
Na okręgu o promieniu  opisano trapez, w którym
opisano trapez, w którym 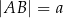 i
i 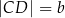 .
.
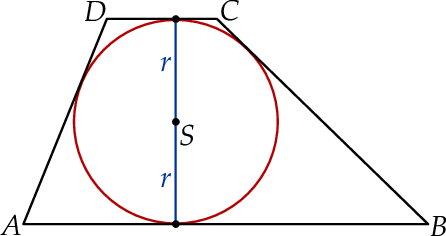
Wykaż, że 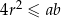 .
.
W trapezie 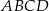 połączono środek
połączono środek 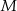 ramienia trapezu
ramienia trapezu 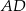 z końcami drugiego ramienia
z końcami drugiego ramienia 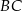 . Wykaż, że pole powstałego trójkąta
. Wykaż, że pole powstałego trójkąta 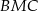 jest równe połowie pola trapezu
jest równe połowie pola trapezu 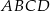 .
.
Punkt 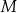 jest środkiem boku
jest środkiem boku 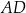 . Udowodnij, że pole trójkąta
. Udowodnij, że pole trójkąta 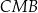 jest połową pola trapezu
jest połową pola trapezu 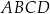 (
(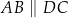 ).
).

W trapez równoramienny o obwodzie 20 i przekątnej długości 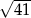 można wpisać okrąg. Oblicz odległości punktu przecięcia przekątnych tego trapezu od prostych zawierających jego boki.
można wpisać okrąg. Oblicz odległości punktu przecięcia przekątnych tego trapezu od prostych zawierających jego boki.
W trapezie równoramiennym 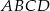 , wysokość
, wysokość 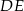 ma długość 6 cm. Punkt
ma długość 6 cm. Punkt 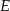 dzieli dłuższą podstawę
dzieli dłuższą podstawę 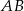 na dwa odcinki. Wiedząc, że
na dwa odcinki. Wiedząc, że 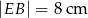 , oblicz pole trapezu
, oblicz pole trapezu 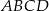 .
.
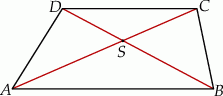
Dwusieczne kątów wewnętrznych trapezu 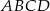 przecinają się w punktach
przecinają się w punktach 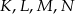 (patrz rysunek). Wykaż, że
(patrz rysunek). Wykaż, że 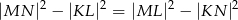 .
.
W trapezie prostokątnym 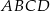 dłuższa podstawa
dłuższa podstawa 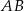 ma długość 8. Przekątna
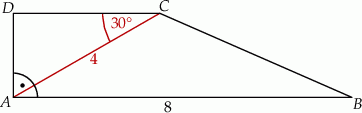
ma długość 8. Przekątna 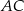 tego trapezu ma długość 4 i tworzy z krótszą podstawą trapezu kąt o mierze
tego trapezu ma długość 4 i tworzy z krótszą podstawą trapezu kąt o mierze 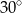 (zobacz rysunek). Oblicz długość przekątnej
(zobacz rysunek). Oblicz długość przekątnej 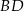 tego trapezu.
tego trapezu.
W trapezie prostokątnym 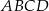 dłuższa podstawa
dłuższa podstawa 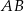 ma długość 15. Przekątna
ma długość 15. Przekątna 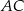 tego trapezu ma długość 6 i tworzy z krótszą podstawą trapezu kąt o mierze
tego trapezu ma długość 6 i tworzy z krótszą podstawą trapezu kąt o mierze 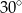 (zobacz rysunek). Oblicz długość przekątnej
(zobacz rysunek). Oblicz długość przekątnej 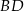 tego trapezu.
tego trapezu.
Dany jest trapez 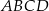 o podstawach
o podstawach 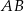 i
i 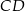 . Przekątne
. Przekątne 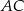 i
i 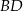 tego trapezu przecinają się w punkcie
tego trapezu przecinają się w punkcie 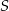 (zobacz rysunek) tak, że
(zobacz rysunek) tak, że 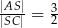 . Pole trójkąta
. Pole trójkąta 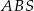 jest równe 12. Oblicz pole trójkąta
jest równe 12. Oblicz pole trójkąta 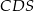 .
.
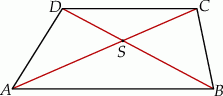
Dany jest trapez 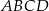 o podstawach
o podstawach 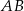 i
i 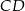 . Przekątne
. Przekątne 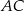 i
i 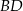 tego trapezu przecinają się w punkcie
tego trapezu przecinają się w punkcie 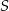 (zobacz rysunek) tak, że
(zobacz rysunek) tak, że 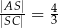 . Pole trójkąta
. Pole trójkąta 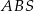 jest równe 24. Oblicz pole trójkąta
jest równe 24. Oblicz pole trójkąta 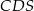 .
.
W trapezie równoramiennym 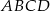 przekątna
przekątna 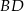 jest prostopadła do ramienia
jest prostopadła do ramienia 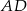 (zobacz rysunek). Podstawy trapezu mają długość:
(zobacz rysunek). Podstawy trapezu mają długość: 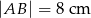 i
i 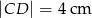 . Oblicz pole oraz miary kątów trapezu.
. Oblicz pole oraz miary kątów trapezu.
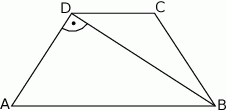
W trapezie równoramiennym 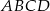 przekątna
przekątna 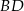 jest prostopadła do ramienia
jest prostopadła do ramienia 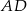 (zobacz rysunek). Podstawy trapezu mają długość:
(zobacz rysunek). Podstawy trapezu mają długość: 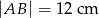 i
i 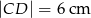 . Oblicz pole oraz miary kątów trapezu.
. Oblicz pole oraz miary kątów trapezu.
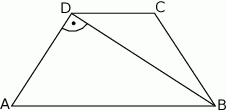
Dany jest trapez prostokątny 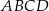 . Podstawa
. Podstawa 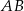 tego trapezu jest równa 26, a ramię
tego trapezu jest równa 26, a ramię 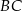 ma długość 24. Przekątna
ma długość 24. Przekątna 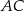 tego trapezu jest prostopadła do ramienia
tego trapezu jest prostopadła do ramienia 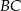 (zobacz rysunek).
(zobacz rysunek).
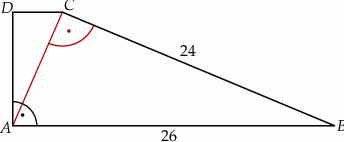
Oblicz długość ramienia 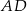 .
.
Oblicz pole i obwód trapezu prostokątnego, w którym podstawy mają długości 13 cm i 22 cm, a tangens kąta ostrego jest równy 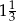 .
.
Przekątne trapezu 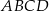 przecinają się w punkcie
przecinają się w punkcie 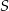 , jego podstawy mają długości
, jego podstawy mają długości 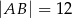 i
i 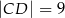 , a wysokość ma długość 8. Punkt
, a wysokość ma długość 8. Punkt 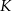 jest środkiem odcinka
jest środkiem odcinka 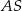 (zobacz rysunek).
(zobacz rysunek).
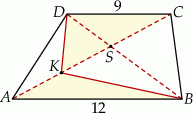
Oblicz stosunek pól trójkątów 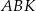 i
i 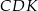 .
.
Przekątne trapezu 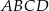 przecinają się w punkcie
przecinają się w punkcie 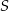 . Promień okręgu opisanego na trójkącie ostrokątnym
. Promień okręgu opisanego na trójkącie ostrokątnym 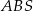 jest o 1 większy od promienia okręgu opisanego na trójkącie
jest o 1 większy od promienia okręgu opisanego na trójkącie 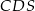 , a długości podstaw trapezu spełniają warunek
, a długości podstaw trapezu spełniają warunek 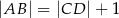 . Wykaż, że
. Wykaż, że