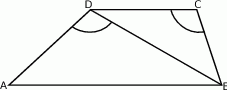
W trapezie 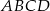 długość podstawy
długość podstawy 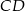 jest równa 18, a długości ramion trapezu
jest równa 18, a długości ramion trapezu 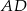 i
i 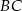 są odpowiednio równe 25 i 15. Kąty
są odpowiednio równe 25 i 15. Kąty  i
i  , zaznaczone na rysunku, mają równe miary. Oblicz obwód tego trapezu.
, zaznaczone na rysunku, mają równe miary. Oblicz obwód tego trapezu.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
W trapezie  długość podstawy
długość podstawy 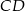 jest równa 18, a długości ramion trapezu
jest równa 18, a długości ramion trapezu 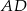 i
i 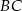 są odpowiednio równe 25 i 15. Kąty
są odpowiednio równe 25 i 15. Kąty 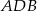 i
i 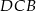 , zaznaczone na rysunku, mają równe miary. Oblicz obwód tego trapezu.
, zaznaczone na rysunku, mają równe miary. Oblicz obwód tego trapezu.

Podstawy trapezu mają długości 10 i 6. Wiedząc, że suma miar kątów wewnętrznych przy dłuższej podstawie jest równa 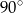 , oblicz długość odcinka łączącego środki podstaw trapezu.
, oblicz długość odcinka łączącego środki podstaw trapezu.
Podstawy trapezu 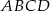 mają długości
mają długości 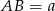 i
i 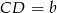 . Na ramionach trapezu wybrano punkty
. Na ramionach trapezu wybrano punkty 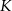 i
i 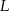 w ten sposób, że odcinek
w ten sposób, że odcinek 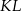 jest równoległy do podstaw i dzieli trapez na dwa trapezy o równych polach. Oblicz długość odcinka
jest równoległy do podstaw i dzieli trapez na dwa trapezy o równych polach. Oblicz długość odcinka 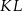 .
.
Jeżeli skrócimy wysokość trapezu o polu 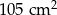 o 2 cm i jednocześnie wydłużymy każdą z jego podstaw o 6 cm, to pole trapezu nie ulegnie zmianie. Wyznacz długość wysokości trapezu (przed zmianą).
o 2 cm i jednocześnie wydłużymy każdą z jego podstaw o 6 cm, to pole trapezu nie ulegnie zmianie. Wyznacz długość wysokości trapezu (przed zmianą).
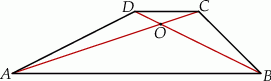
W trapezie 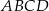 (
(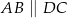 ) przekątne
) przekątne 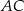 i
i 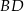 przecinają się w punkcie
przecinają się w punkcie 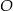 takim, że
takim, że 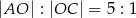 . Pole trójkąta
. Pole trójkąta 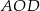 jest równe 10. Uzasadnij, że pole trapezu
jest równe 10. Uzasadnij, że pole trapezu 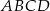 jest równe 72.
jest równe 72.
W trapezie 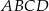 (
(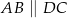 ) przekątne
) przekątne 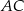 i
i 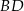 przecinają się w punkcie
przecinają się w punkcie 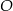 takim, że
takim, że 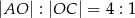 . Pole trójkąta
. Pole trójkąta 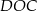 jest równe 2. Uzasadnij, że pole trapezu
jest równe 2. Uzasadnij, że pole trapezu  jest równe 50.
jest równe 50.
Czworokąt 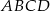 jest trapezem o podstawach
jest trapezem o podstawach 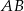 i
i 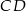 . Wykaż że
. Wykaż że
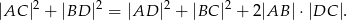
Jedna z podstaw trapezu wpisanego w okrąg jest średnicą okręgu. Oblicz cosinus kąta ostrego trapezu wiedząc, że stosunek obwodu trapezu do sumy długości jego podstaw wynosi 3:2.
W trapezie równoramiennym 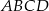 przekątna
przekątna 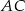 jest prostopadła do ramienia i tworzy z dłuższą podstawą
jest prostopadła do ramienia i tworzy z dłuższą podstawą 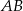 trapezu kąt o mierze
trapezu kąt o mierze 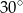 . Oblicz pole powierzchni tego trapezu wiedząc, że długość przekątnej
. Oblicz pole powierzchni tego trapezu wiedząc, że długość przekątnej 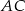 wynosi
wynosi 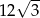 .
.
W trapezie równoramiennym 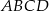 przekątna
przekątna 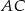 jest prostopadła do ramienia. Kąt ostry trapezu ma miarę
jest prostopadła do ramienia. Kąt ostry trapezu ma miarę 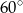 . Oblicz pole powierzchni tego trapezu wiedząc, że długość przekątnej
. Oblicz pole powierzchni tego trapezu wiedząc, że długość przekątnej 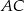 wynosi
wynosi 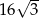 .
.
Ramiona trapezu opisanego na okręgu mają długości 3 cm i 5 cm. Odcinek łączący środki ramion dzieli trapez na dwie figury, których stosunek pól wynosi 5:11. Oblicz długości podstaw trapezu.
W trapezie opisanym na okręgu ramiona mają długości 6 i 10. Odcinek łączący środki tych ramion dzieli trapez na dwie części, których pola pozostają w stosunku 5:11. Wyznacz długości podstaw tego trapezu.
W trapezie opisanym na okręgu boki nierównoległe mają długości 3 i 5, zaś odcinek łączący środki tych boków dzieli trapez na dwie części, których pola są w stosunku 5:11. Oblicz długości podstaw trapezu.
Pole trapezu równoramiennego opisanego na okręgu jest równe 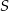 , a kąt ostry przy podstawie ma miarę
, a kąt ostry przy podstawie ma miarę  . Wykaż, że ramię tego trapezu ma długość
. Wykaż, że ramię tego trapezu ma długość 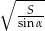 .
.
W pewnym trapezie kąty przy dwóch przeciwległych wierzchołkach mają miary  oraz
oraz 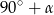 . Jedno z ramion tego trapezu ma długość
. Jedno z ramion tego trapezu ma długość 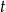 . Wyznacz różnicę długości podstaw tego trapezu.
. Wyznacz różnicę długości podstaw tego trapezu.
Podstawy trapezu 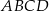 mają długości
mają długości 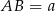 i
i 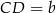 . Oblicz długość odcinka łączącego środki ramion trapezu.
. Oblicz długość odcinka łączącego środki ramion trapezu.
Trapez równoramienny o podstawach długości  i
i 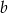 opisany jest na okręgu. Oblicz pole koła, którego brzegiem jest okrąg wpisany w ten trapez.
opisany jest na okręgu. Oblicz pole koła, którego brzegiem jest okrąg wpisany w ten trapez.
Proste zawierające ramiona 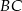 i
i 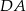 trapezu
trapezu 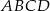 przecinają się w punkcie
przecinają się w punkcie  . Dane są:
. Dane są: 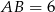 ,
, 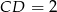 oraz obwód trójkąta
oraz obwód trójkąta 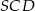 równy
równy 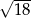 . Oblicz obwód trójkąta
. Oblicz obwód trójkąta 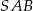 .
.
Oblicz wysokość i przekątną trapezu równoramiennego o podstawach 21 cm i 11 cm oraz ramieniu równym 13 cm.
Przekątne trapezu przecinają się w punkcie 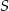 . Przez punkt
. Przez punkt 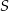 poprowadzono prostą równoległą do podstaw trapezu, która przecina ramiona trapezu w punktach
poprowadzono prostą równoległą do podstaw trapezu, która przecina ramiona trapezu w punktach 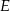 i
i 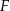 . Wykaż, że
. Wykaż, że 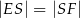 .
.
W trapezie 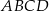 o podstawach
o podstawach 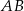 i
i 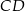 przez punkt
przez punkt 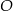 przecięcia się przekątnych poprowadzono dwie proste równoległe do boków
przecięcia się przekątnych poprowadzono dwie proste równoległe do boków 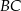 i
i 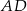 . Prosta równoległa do boku
. Prosta równoległa do boku 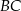 przecina bok
przecina bok 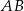 w punkcie
w punkcie 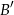 , a prosta równoległa do boku
, a prosta równoległa do boku 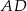 przecina bok
przecina bok 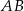 w punkcie
w punkcie 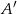 . Wykaż, że
. Wykaż, że 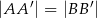 .
.
W trapezie równoramiennym 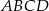 ramię ma długość 10. Obwód tego trapezu jest równy 40. Wiedząc, że tangens kąta ostrego w trapezie
ramię ma długość 10. Obwód tego trapezu jest równy 40. Wiedząc, że tangens kąta ostrego w trapezie 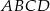 jest równy
jest równy  , oblicz długości jego podstaw.
, oblicz długości jego podstaw.
W trapezie równoramiennym 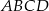 ramię ma długość 13. Obwód tego trapezu jest równy 52. Wiedząc, że tangens kąta ostrego w trapezie
ramię ma długość 13. Obwód tego trapezu jest równy 52. Wiedząc, że tangens kąta ostrego w trapezie 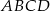 jest równy
jest równy 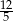 , oblicz długości jego podstaw.
, oblicz długości jego podstaw.
Punkt styczności okręgu o promieniu  wpisanego w trapez równoramienny dzieli ramię trapezu w stosunku 1:2. Oblicz promień okręgu opisanego na tym trapezie.
wpisanego w trapez równoramienny dzieli ramię trapezu w stosunku 1:2. Oblicz promień okręgu opisanego na tym trapezie.
Punkt styczności okręgu o promieniu  wpisanego w trapez równoramienny dzieli ramię trapezu w stosunku 2:5. Oblicz promień okręgu opisanego na tym trapezie.
wpisanego w trapez równoramienny dzieli ramię trapezu w stosunku 2:5. Oblicz promień okręgu opisanego na tym trapezie.
Środek okręgu wpisanego w trapez prostokątny, znajduje się w odległości 4 oraz 8 od końców dłuższego ramienia trapezu. Oblicz pole tego trapezu.
Środek okręgu wpisanego w trapez prostokątny znajduje się w odległości 2 cm i 4 cm od końców ramienia pochyłego danego trapezu. Znaleźć pole trapezu.
W trapezie 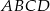 o podstawach
o podstawach 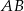 i
i 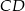 dane są długości przekątnych
dane są długości przekątnych 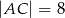 i
i 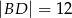 oraz pola
oraz pola 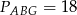 i
i 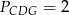 . Punkty
. Punkty 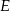 i
i 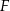 są środkami odpowiednio przekątnych
są środkami odpowiednio przekątnych 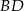 i
i 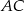 .
.
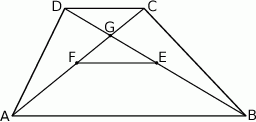
Oblicz pole trapezu 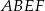 .
.
W trapezie 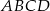 o podstawach
o podstawach 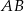 i
i 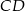 dane są długości przekątnych
dane są długości przekątnych 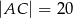 i
i 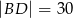 oraz pola
oraz pola 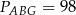 i
i 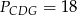 . Punkty
. Punkty 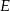 i
i 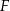 są środkami odpowiednio przekątnych
są środkami odpowiednio przekątnych 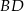 i
i 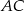 .
.
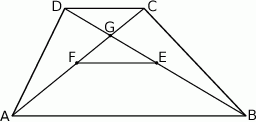
Oblicz pole trójkąta 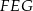 .
.
