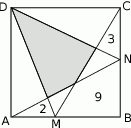
Moneta o średnicy 1 cm toczy się po obwodzie sześciokąta foremnego o boku długości 1 cm (patrz rysunek) tak długo, aż powróci do położenia początkowego. Ile centymetrów ma długość drogi, którą zakreślił środek monety?
A) 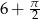 B)
B) 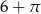 C)
C) 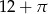 D)
D) 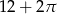 E)
E) 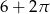

 ?
? 
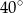
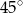
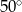
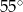
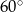
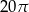
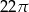
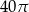
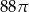
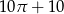
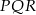 , jeśli
, jeśli 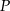 jest wierzchołkiem prostokąta, a
jest wierzchołkiem prostokąta, a 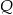 i
i 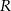 punktami styczności?
punktami styczności? 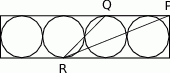
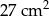
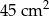
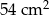
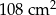
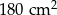
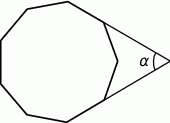
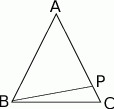
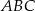 długość dwusiecznej
długość dwusiecznej 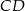 kąta przy wierzchołku
kąta przy wierzchołku 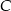 jest równa długości podstawy
jest równa długości podstawy 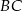 . Ile jest równa miara kąta
. Ile jest równa miara kąta 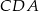 ?
?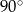
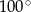
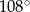
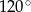
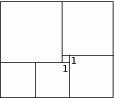
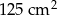 podzielono na pięć części o równych polach. Cztery z nich to kwadraty, a piąta to sześciokąt w kształcie litery L. Jaka jest długość najkrótszego boku tego sześciokąta?
podzielono na pięć części o równych polach. Cztery z nich to kwadraty, a piąta to sześciokąt w kształcie litery L. Jaka jest długość najkrótszego boku tego sześciokąta? 
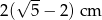
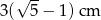
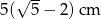
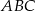 (
(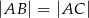 ), w którym
), w którym 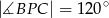 i
i 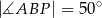 . Jaka jest miara kąta
. Jaka jest miara kąta 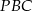 ?
? 
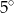
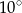
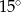
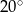
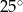
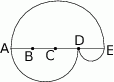
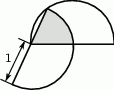
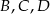 dzielą odcinek
dzielą odcinek 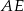 na cztery równe części. Narysowane trzy łuki są półokręgami o średnicach odpowiednio
na cztery równe części. Narysowane trzy łuki są półokręgami o średnicach odpowiednio 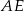 ,
, 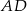 i
i 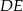 . Jaki jest stosunek długości półokręgu
. Jaki jest stosunek długości półokręgu 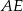 do sumy długości półokręgów
do sumy długości półokręgów 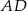 i
i 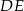 ?
? 
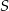 i
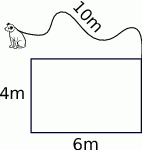
i 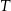 i owe węzły po naprężeniu linki tworzyły trójkąt prostokątny. Na takiej lince długości 12m węzeł
i owe węzły po naprężeniu linki tworzyły trójkąt prostokątny. Na takiej lince długości 12m węzeł 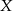 jest w odległości 3m od końca
jest w odległości 3m od końca 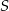 . W jakiej odległości od końca
. W jakiej odległości od końca 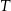 jest drugi węzeł, jeżeli po złączeniu końców otrzymujemy kąt prosty w węźle
jest drugi węzeł, jeżeli po złączeniu końców otrzymujemy kąt prosty w węźle 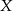 ?
? 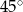 (rysunek obok). Do której łuzy wpadnie?
(rysunek obok). Do której łuzy wpadnie? 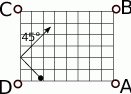
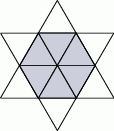
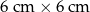 i trójkąt. Jeżeli położę kwadrat na trójkącie, to mogę pokryć co najwyżej 60% powierzchni trójkąta. Jeżeli zaś położę trójkąt na kwadracie, to mogę pokryć co najwyżej
i trójkąt. Jeżeli położę kwadrat na trójkącie, to mogę pokryć co najwyżej 60% powierzchni trójkąta. Jeżeli zaś położę trójkąt na kwadracie, to mogę pokryć co najwyżej  powierzchni kwadratu. Pole trójkąta jest równe
powierzchni kwadratu. Pole trójkąta jest równe 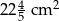
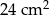
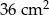
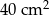
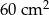
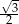


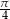
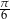
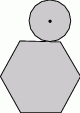
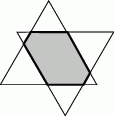
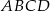 . Odcinki poprowadzone z punktów
. Odcinki poprowadzone z punktów 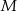 i
i 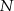 do jego wierzchołków dzielą go na osiem części. Na rysunku zaznaczono pola trzech z nich. Jakie jest pole zacieniowanej części?
do jego wierzchołków dzielą go na osiem części. Na rysunku zaznaczono pola trzech z nich. Jakie jest pole zacieniowanej części?