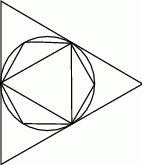
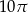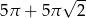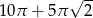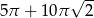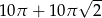Trójkąt równoboczny i sześciokąt foremny wpisano w okrąg, na którym opisano trójkąt równoboczny (patrz rysunek). Niech 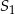 oznacza pole dużego trójkąta,
oznacza pole dużego trójkąta, 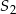 pole małego trójkąta, a
pole małego trójkąta, a 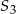 pole sześciokąta foremnego. Która z równości jest prawdziwa?
pole sześciokąta foremnego. Która z równości jest prawdziwa?
A) 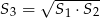 B)
B) 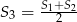 C)
C) 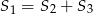 D)
D) 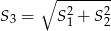 E)
E) 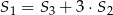


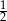
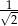
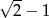
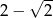
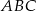 , w którym
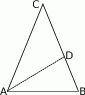
, w którym 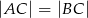 , poprowadzono dwusieczną
, poprowadzono dwusieczną 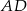 kąta przy wierzchołku
kąta przy wierzchołku 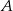 (patrz rysunek), przy czym
(patrz rysunek), przy czym 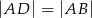 . Jaka jest miara kąta
. Jaka jest miara kąta 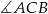 ?
? 
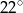
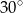
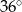
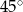
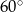
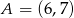 ,
, 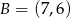 ,
, 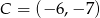 ,
, 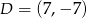 i
i 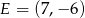 . Który z poniższych odcinków jest równoległy do osi
. Który z poniższych odcinków jest równoległy do osi 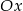 ?
?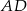
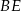
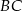
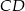
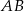

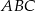 i
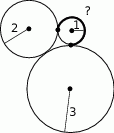
i 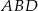 zostały wpisane w okrąg, jak na rysunku obok. Wiadomo, że
zostały wpisane w okrąg, jak na rysunku obok. Wiadomo, że 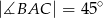 oraz
oraz 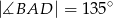 . Wówczas długości cięciw
. Wówczas długości cięciw 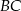 i
i 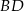 spełniają zależność
spełniają zależność 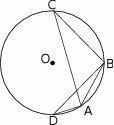
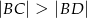
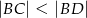
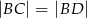
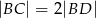
 ?
? 

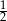
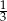
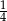
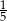
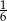
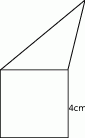
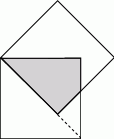
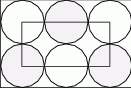
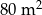 , a promień każdego okręgu w środku w jego wierzchołku jest równy 2 m. Ile metrów kwadratowych ma pole zacieniowanej figury?
, a promień każdego okręgu w środku w jego wierzchołku jest równy 2 m. Ile metrów kwadratowych ma pole zacieniowanej figury? 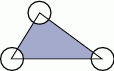
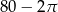
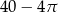
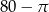
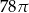
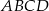 w punktach
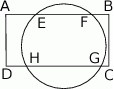
w punktach 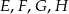 , jak na rysunku obok. Wiadomo, że
, jak na rysunku obok. Wiadomo, że 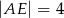 ,
, 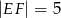 ,
, 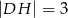 . Ile wynosi długość odcinka
. Ile wynosi długość odcinka 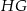 ?
? 
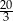
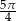
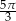
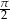
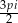
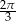
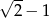
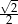
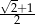
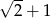
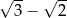
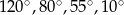 . Jaka jest miara najmniejszego kąta w trójkącie ostrokątnym?
. Jaka jest miara najmniejszego kąta w trójkącie ostrokątnym?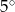
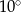
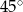
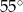

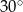
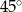
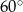
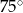
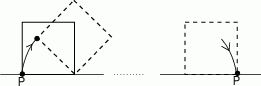
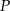 ponownie znajdzie się na tej prostej. Jaka jest długość drogi, którą zakreślił punkt
ponownie znajdzie się na tej prostej. Jaka jest długość drogi, którą zakreślił punkt 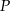 ?
?