Z dwóch przeciwległych wierzchołków kwadratu o boku 2 zakreślono okręgi o promieniu 2. Oblicz pole „soczewki” wyznaczonej przez te okręgi.
/Szkoła podstawowa
Dany jest wzór opisujący pole trapezu: 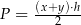 , gdzie
, gdzie  i
i 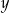 oznaczają długości podstaw trapezu, a
oznaczają długości podstaw trapezu, a 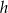 oznacza wysokość trapezu. Którym równaniem opisano
oznacza wysokość trapezu. Którym równaniem opisano  wyznaczone poprawnie z tego wzoru?
wyznaczone poprawnie z tego wzoru?
A) 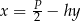 B)
B) 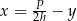 C)
C) 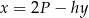 D)
D) 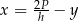
Rozpuszczono 30g soli w 210g wody. Oblicz procentowe stężenie soli w tym roztworze.
W pewnej grupie przyjaciół co czwarta osoba ma na imię Kuba. Losujemy jedną osobę z tej grupy. Prawdopodobieństwo tego, że wylosowana osoba nie ma na imię Kuba, jest równe
A) 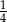 B)
B) 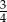 C)
C) 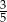 D)
D) 
Suma siedemdziesięciu czterech liczb dodatnich jest równa 1978. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Po zmniejszeniu każdej z tych liczb o 6 suma otrzymanych liczb będzie równa 1536. | P | F |
| Po zwiększeniu każdej z tych liczb o 50% suma otrzymanych liczb będzie równa 2967. | P | F |
Asi zerwał się naszyjnik. Trzecią część liczby korali znalazła na podłodze, jedną czwartą w kieszeni, jedną piątą pod oparciem kanapy, a szósta część liczby korali została na sznurku. Sześciu korali nie udało się jej odnaleźć. Oblicz, ile korali zostało na sznurku.
Dany jest prostokąt o bokach  i
i 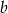 . Zmniejszamy długość boku
. Zmniejszamy długość boku  o 10% oraz zwiększamy długość boku
o 10% oraz zwiększamy długość boku 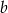 o 20%.
o 20%.
- O ile procent zwiększy się pole tego prostokąta?
- Wyznacz długość boku
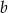 , dla której nowy prostokąt będzie miał taki sam obwód jak prostokąt wyjściowy, jeśli wiadomo, że bok
, dla której nowy prostokąt będzie miał taki sam obwód jak prostokąt wyjściowy, jeśli wiadomo, że bok  ma długość 30 cm.
ma długość 30 cm.
Na rysunkach przedstawiono kształt i sposób układania płytek oraz niektóre wymiary w centymetrach.
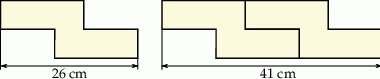
Ułożono wzór z 6 płytek, jak na rysunku.

Odcinek  ma długość
ma długość
A) 101 cm B) 156 cm C) 123 cm D) 90 cm
Asia trenuje kolarstwo. Trasa, którą pokonała w ciągu 4 godzin, wiodła leśną drogą, ścieżką rowerową, a następnie polną drogą i chodnikiem. Na diagramie przedstawiono w procentach czas jazdy Asi po leśnej drodze, ścieżce rowerowej i polnej drodze, ale nie narysowano słupka z informacją dotyczącą jazdy po chodniku.
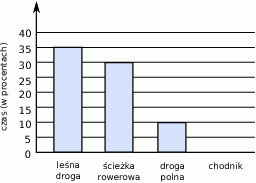
Jaki procent czasu Asia jechała po chodniku?
A) 10% B) 15% C) 20% D) 25%
Asia trenuje kolarstwo. Trasa, którą pokonała w ciągu 4 godzin, wiodła leśną drogą, ścieżką rowerową, a następnie polną drogą i chodnikiem. Na diagramie przedstawiono w procentach czas jazdy Asi po leśnej drodze, ścieżce rowerowej i polnej drodze, ale nie narysowano słupka z informacją dotyczącą jazdy po chodniku.
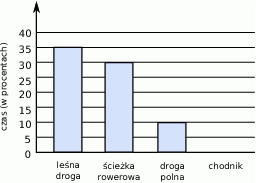
Ile minut Asia jechała leśną drogą?
A) 60 minut B) 72 minuty C) 84 minuty D) 96 minut
Wiadomo, że mediana liczb 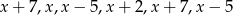 jest równa średniej tych liczb. Zatem liczba
jest równa średniej tych liczb. Zatem liczba 
A) jest równa 3 B) jest równa 4 C) jest równa 5 D) może mieć dowolną wartość
Wiadomo, że mediana liczb 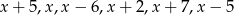 jest dwa razy większa od średniej tych liczb. Zatem liczba
jest dwa razy większa od średniej tych liczb. Zatem liczba 
A) jest równa 0 B) jest równa 1 C) jest równa 2 D) może mieć dowolną wartość
W pewnej klasie dziewczęta stanowiły 25% liczby uczniów. Do klasy przybyła jedna osoba i wówczas odsetek dziewcząt wzrósł do 28%. Ilu chłopców jest w tej klasie?
Która z podanych liczb jest największa?
A) 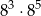 B)
B) 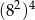 C)
C) 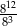 D)
D) 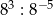
Dane są liczby

Która z tych liczb jest największa?
A) I B) II C) III D) IV
Która z podanych liczb jest największa?
A) 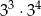 B)
B) 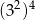 C)
C) 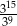 D)
D) 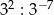
Która z podanych liczb jest największa?
A) 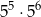 B)
B) 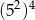 C)
C) 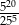 D)
D) 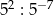
Dane są liczby

Która z tych liczb jest największa?
A) I B) II C) III D) IV
Pociąg przebył ze stałą prędkością drogę 700 metrów w czasie 50 sekund. Przy zachowaniu tej samej, stałej prędkości ten sam pociąg drogę równą jego długości przebył w czasie 15 sekund. Oblicz długość tego pociągu.
Pociąg przebył ze stałą prędkością drogę 900 metrów w czasie 75 sekund. Przy zachowaniu tej samej, stałej prędkości ten sam pociąg drogę równą jego długości przebył w czasie 16 sekund. Oblicz długość tego pociągu.
Rozwiąż nierówność: 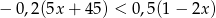 .
.
Rozwiąż nierówność 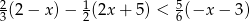 .
.
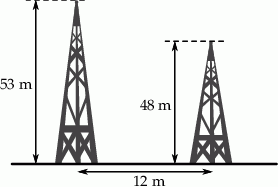
Dwa stalowe maszty o wysokościach 48 m i 53 m stoją w odległości 12 metrów od siebie. Czubki tych masztów postanowiono połączyć stalową liną, której 1 metr waży 500 g. Jaka będzie waga liny łączącej czubki masztów? Wynik podaj w kilogramach. Zapisz obliczenia.
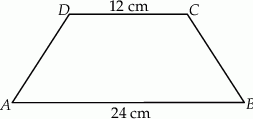
Podstawy trapezu równoramiennego 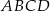 mają długości: 12 cm i 24 cm. Pole tego trapezu jest równe
mają długości: 12 cm i 24 cm. Pole tego trapezu jest równe 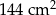 . Oblicz obwód trapezu
. Oblicz obwód trapezu 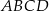 .
.
Na rysunku przedstawiono skład jednego ze stopów miedzi, mosiądzu, który jest wykorzystywany głównie do odlewania przedmiotów ozdobnych. Ile potrzeba cynku do odlania 2000 kg ozdób?

A) 1600 kg B) 400 kg C) 600 kg D) 750 kg
Na rysunku przedstawiono skład jednego ze stopów miedzi, zwanego „złotem mainnheimskim”, który jest wykorzystywany do wyrobu sztucznej biżuterii. Ile potrzeba cynku do wykonania 1500 kg biżuterii?

A) 135 kg B) 1200 kg C) 600 kg D) 165 kg
Na rysunku przedstawiono skład jednego ze stopów miedzi, brązu, który jest wykorzystywany między innymi do odlewania dzwonów. Ile potrzeba miedzi do odlania dzwonu ważącego 10000 kg?

A) 76 kg B) 2400 kg C) 4800 kg D) 7600 kg
Właściciel sklepu sportowego kupił w hurtowni deskorolki i kaski. Cena hurtowa deskorolki była o 60 zł wyższa niż cena hurtowa kasku. Właściciel sklepu ustalił cenę sprzedaży deskorolki o 20% wyższą od ceny hurtowej, a cenę sprzedaży kasku – o 40% wyższą od ceny hurtowej. Deskorolka i kask łącznie kosztowały w sklepie 397 zł. Oblicz łączny koszt zakupu po cenach hurtowych jednej deskorolki i jednego kasku. Zapisz obliczenia.
Właściciel sklepu komputerowego kupił w hurtowni klawiatury i myszki. Cena hurtowa klawiatury była o 30 zł wyższa niż cena hurtowa myszki. Właściciel sklepu ustalił cenę sprzedaży klawiatury o 10% wyższą od ceny hurtowej, a cenę sprzedaży myszki – o 30% wyższą od ceny hurtowej. Klawiatura i myszka łącznie kosztowały w sklepie 213 zł. Oblicz łączny koszt zakupu po cenach hurtowych jednej klawiatury i jednej myszki. Zapisz obliczenia.
Jacek otrzymał kieszonkowe, które w całości wydał w ciągu czterech kolejnych tygodni. W pierwszym tygodniu wydał  całej kwoty, w drugim tygodniu
całej kwoty, w drugim tygodniu 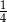 pozostałej kwoty, w trzecim tygodniu wydał dwa razy więcej pieniędzy niż w drugim tygodniu. W czwartym tygodniu wydał pozostałe 75 zł. Jeżeli przez
pozostałej kwoty, w trzecim tygodniu wydał dwa razy więcej pieniędzy niż w drugim tygodniu. W czwartym tygodniu wydał pozostałe 75 zł. Jeżeli przez  oznaczymy kwotę kieszonkowego, którą otrzymał Jacek, to sytuację przedstawioną w zadaniu opisuje równanie
oznaczymy kwotę kieszonkowego, którą otrzymał Jacek, to sytuację przedstawioną w zadaniu opisuje równanie
A) 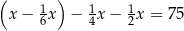
B) 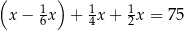
C) 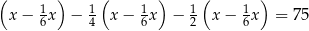
D) 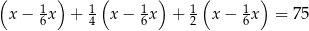
W trójkącie równoramiennym 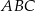 , w którym
, w którym 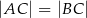 i
i 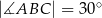 poprowadzono wysokość
poprowadzono wysokość 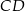 i dwusieczną kąta
i dwusieczną kąta 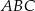 przecinającą bok
przecinającą bok 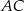 w punkcie
w punkcie 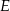 . Wysokość i dwusieczna przecinają się w punkcie
. Wysokość i dwusieczna przecinają się w punkcie 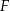 .
.
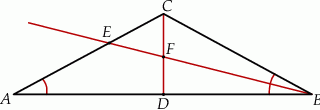
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
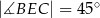 | P | F |
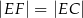 | P | F |
W trójkącie równoramiennym 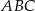 , w którym
, w którym 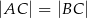 i
i 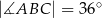 poprowadzono wysokość
poprowadzono wysokość 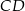 i dwusieczną kąta
i dwusieczną kąta 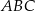 przecinającą bok
przecinającą bok 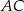 w punkcie
w punkcie 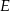 . Wysokość i dwusieczna przecinają się w punkcie
. Wysokość i dwusieczna przecinają się w punkcie  .
.
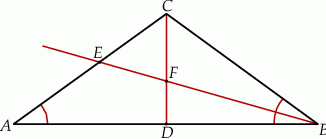
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
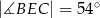 | P | F |
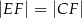 | P | F |
W trójkącie 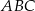 , w którym
, w którym 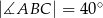 ,
, 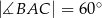 poprowadzono dwusieczne
poprowadzono dwusieczne 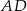 i
i 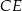 , które przecinają się w punkcie
, które przecinają się w punkcie 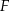 .
.
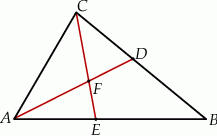
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
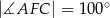 | P | F |
 | P | F |

