Na przekątnej 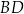 kwadratu
kwadratu 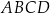 o boku długości 4 zbudowano trójkąt równoboczny
o boku długości 4 zbudowano trójkąt równoboczny 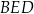 .
.
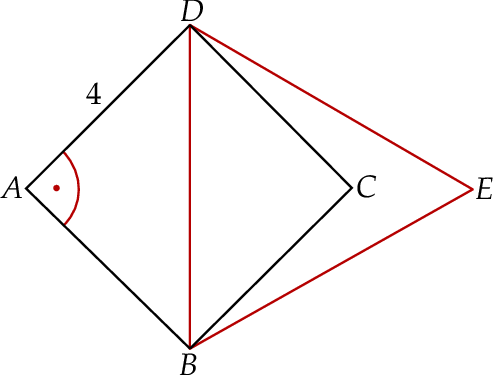
Pole trójkąta 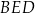 jest równe
jest równe
A) 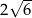 B)
B) 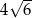 C)
C) 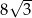 D)
D) 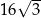
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Na przekątnej 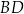 kwadratu
kwadratu 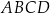 o boku długości 4 zbudowano trójkąt równoboczny
o boku długości 4 zbudowano trójkąt równoboczny 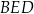 .
.

Pole trójkąta 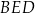 jest równe
jest równe
A) 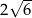 B)
B) 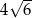 C)
C) 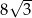 D)
D) 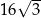
Oblicz długości odcinka 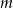 .
.
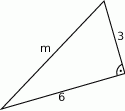
Oblicz długości odcinka 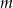 .
.
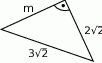
Oblicz długości odcinka 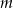 .
.
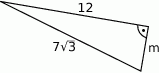
Na poniższym wykresie przedstawiono jak zmieniała się liczba ludności Europy i Afryki w latach 1950–2010 (wykresy mają różne osie pionowe).
Wskaż zdanie prawdziwe.
A) W roku 2000 Europa liczyła więcej mieszkańców niż Afryka
B) W 1990 roku w Afryce mieszkało około 600 mln ludzi
C) W całym przedstawionym okresie w Europie mieszkało mniej osób niż w Afryce
D) W latach 1950-2010 liczba mieszkańców Afryki podwoiła się
Zosia zebrała 2 kg malin i wsypała je do trzech takich samych pojemników. Masa pustego pojemnika była równa 0,05 kg. Pierwszy pojemnik z malinami miał masę 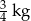 , a masa drugiego pojemnika z malinami była równa 0,70 kg. Ile malin wsypała Zosia do trzeciego pojemnika?
, a masa drugiego pojemnika z malinami była równa 0,70 kg. Ile malin wsypała Zosia do trzeciego pojemnika?
A) 0,45 kg B) 0,55 kg C) 0,60 kg D) 0,65 kg
Oblicz długości boków prostokąta o obwodzie 1,1 dm którego boki są proporcjonalne do odcinków długości 4 cm i 7 cm.
Na rysunku przedstawiono fragment siatki ostrosłupa prawidłowego czworokątnego.
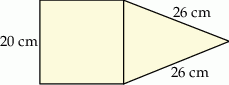
Suma długości krawędzi bocznych tego ostrosłupa jest równa A/B.
A) 360 cm B) 104 cm
Pole powierzchni całkowitej tego ostrosłupa jest równa C/D.
C) 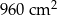 D)
D) 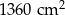
Trójkąt równoboczny, kwadrat i sześciokąt foremny mają ten sam obwód długości 10cm. Oblicz pole każdej z tych figur. Która z nich ma największe pole, a która najmniejsze?
Ania chciała kupić 10 jednakowych puszek karmy dla psa, ale zabrakło jej 11 złotych. Kupiła 6 takich puszek karmy i zostało jej 3,40 złotych. Ile kosztuje jedna puszka karmy?
Adrian chciał kupić 12 jednakowych butelek soku owocowego, ale zabrakło mu 23,80 złotych. Kupił więc 8 butelek soku i zostało mu 5,80 złotego. Ile kosztuje jedna butelka tego soku?
W klasie jest o 25% więcej chłopców niż dziewcząt. Jaką część wszystkich uczniów tej klasy stanowią chłopcy?
A) 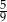 B)
B) 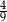 C)
C) 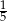 D)
D) 
W klasie jest o 15% więcej chłopców niż dziewcząt. Jaką część wszystkich uczniów tej klasy stanowią chłopcy?
A) 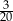 B)
B) 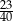 C)
C) 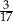 D)
D) 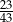
Dziewczęta stanowią 30% uczniów w pewnej klasy. Wynika stąd, że chłopcy stanowią
A) 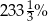 liczby dziewcząt B)
liczby dziewcząt B) 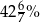 liczby dziewcząt
liczby dziewcząt
C) 21% liczby dziewcząt D) 70% liczby dziewcząt
Chłopcy stanowią 25% uczniów w pewnej klasy. Wynika stąd, że dziewczęta stanowią
A) 175% liczby chłopców B) 200% liczby chłopców
C) 75% liczby chłopców D) 300% liczby chłopców
Dziewczęta stanowią 40% uczniów w pewnej klasy. Wynika stąd, że chłopcy stanowią
A) 50% liczby dziewcząt B) 150% liczby dziewcząt
C) 60% liczby dziewcząt D) 120% liczby dziewcząt
W układzie współrzędnych zaznaczono trzy kolejne wierzchołki równoległoboku.
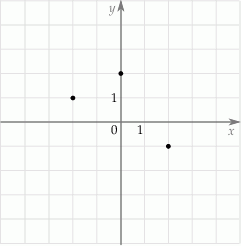
Który z punktów nie może być czwartym wierzchołkiem tego równoległoboku?
A) 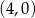 B)
B) 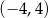 C)
C) 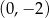 D)
D) 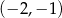
Oblicz miarę kąta  .
.
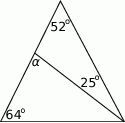
Oblicz miarę kąta  .
.
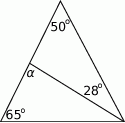
Oblicz miarę kąta  .
.
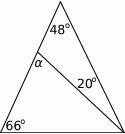
Oblicz miarę kąta  .
.
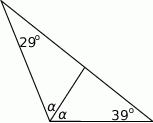
Oblicz miarę kąta  .
.
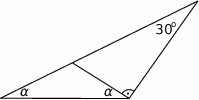
Oblicz miarę kąta  .
.
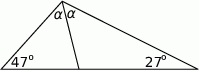
Oblicz miarę kąta  .
.
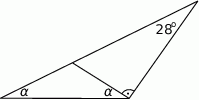
Oblicz miarę kąta  .
.
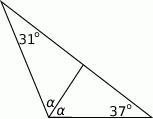
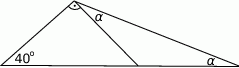
Oblicz miarę kąta  .
.
W pudełku są trzy rodzaje piłek: czerwone, niebieskie i zielone. Czerwonych piłek jest trzy razy więcej niż niebieskich, a zielonych jest dwa razy mniej niż czerwonych. Losujemy jedną piłkę. Prawdopodobieństwo, że wylosujemy piłkę zieloną, jest równe
A) 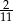 B)
B) 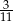 C)
C) 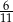 D)
D) 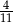
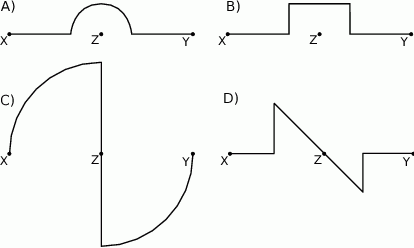
Piechur szedł z punktu 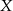 do punktu
do punktu 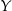 ze stałą prędkością. Na wykresie poniżej zilustrowano, jak zmieniała się odległość piechura od punktu
ze stałą prędkością. Na wykresie poniżej zilustrowano, jak zmieniała się odległość piechura od punktu 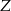 .
.
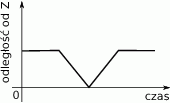
Na którym z poniższych rysunków zilustrowano, jak mogła wyglądać trasa piechura pomiędzy punktami 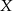 i
i  ?
?
Znajdź liczbę, której 3% wynosi 16.
Maturzysta na rozwiązanie testu składającego się z 34 zadań przeznaczył 169 minut, przy czym na rozwiązanie każdego z 9 zadań otwartych przeznaczył trzy razy więcej czasu niż na rozwiązanie każdego z zdań zamkniętych. Średnia liczba sekund przeznaczonych na jedno zadanie zamknięte jest równa
A) 180 B) 205 C) 195 D) 170
Do sklepu warzywno-owocowego zakupiono w hurtowni 250 kg pomidorów za 800 zł. Pierwszego dnia sprzedano 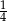 ilości kupionego towaru, drugiego dnia o 5,5 kg więcej niż pierwszego, a trzeciego dnia
ilości kupionego towaru, drugiego dnia o 5,5 kg więcej niż pierwszego, a trzeciego dnia 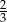 tej ilości, którą sprzedano pierwszego i drugiego dnia razem. Ile kilogramów pomidorów zostało w sklepie? Jaki był zysk z trzydniowej sprzedaży warzyw, jeżeli cena detaliczna 1 kilograma pomidorów stanowi 1,25 ceny hurtowej?
tej ilości, którą sprzedano pierwszego i drugiego dnia razem. Ile kilogramów pomidorów zostało w sklepie? Jaki był zysk z trzydniowej sprzedaży warzyw, jeżeli cena detaliczna 1 kilograma pomidorów stanowi 1,25 ceny hurtowej?
Dane są trzy wyrażenia:
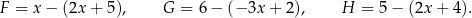
Dla każdej wartości  prawdziwa jest równość
prawdziwa jest równość
A) 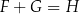 B)
B) 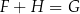 C)
C) 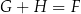 D)
D) 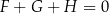
W trapezie 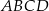 mamy
mamy 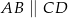 oraz
oraz 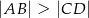 . Punkt
. Punkt 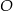 jest środkiem ramienia
jest środkiem ramienia 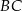 , a punkt
, a punkt 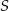 jest punktem wspólnym prostych
jest punktem wspólnym prostych 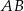
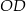 . Udowodnij, że pole trójkąta
. Udowodnij, że pole trójkąta 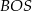 jest równe polu trójkąta
jest równe polu trójkąta 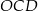 .
.
Liczby 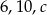 są długościami boków trójkąta równoramiennego. Oblicz
są długościami boków trójkąta równoramiennego. Oblicz  .
.
