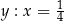Dane są dwie liczby  i
i 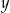 . Wiadomo, że
. Wiadomo, że 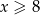 oraz
oraz 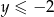 .
.
![]()
Najmniejsza możliwa wartość różnicy 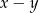 jest równa:
jest równa:
A) 10 B) 6 C) 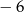 D)
D) 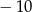
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Dane są dwie liczby  i
i 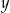 . Wiadomo, że
. Wiadomo, że 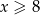 oraz
oraz 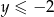 .
.
![]()
Najmniejsza możliwa wartość różnicy 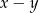 jest równa:
jest równa:
A) 10 B) 6 C) 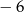 D)
D) 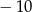
Dane są dwie liczby  i
i 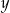 . Wiadomo, że
. Wiadomo, że 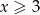 oraz
oraz 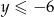 .
.
![]()
Najmniejsza możliwa wartość różnicy 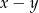 jest równa:
jest równa:
A) 3 B) 9 C) 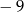 D)
D) 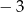
Dane są dwie liczby  i
i 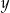 . Wiadomo, że
. Wiadomo, że 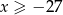 oraz
oraz 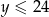 .
.
![]()
Największa możliwa wartość różnicy 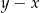 jest równa:
jest równa:
A) 0 B) 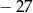 C) 51 D) 24
C) 51 D) 24
Dana jest liczba 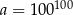 . Liczba
. Liczba 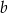 stanowi 1% liczby
stanowi 1% liczby  . Wówczas
. Wówczas
A) 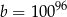 B)
B) 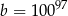 C)
C) 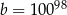 D)
D) 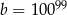
Płyta kosztowała 80 zł, a po obniżce 60 zł. O ile procent obniżono cenę płyty?
A) 20% B) 25% C) 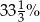 D) 75%
D) 75%
Narty kosztowały 680 zł. O ile procent należałoby obniżyć cenę nart, aby kosztowały 595 zł?
A) 8,5% B) 12,5% C) 14,2% D) 25%
Odtwarzacz kosztujący 340 zł sprzedano podczas wyprzedaży za 255 zł. Obniżka wynosiła
A) 15% B) 20% C) 40% D) 25%
Buty, które kosztowały 220 złotych, przeceniono i sprzedano za 176 złotych. O ile procent obniżono cenę butów?
A) 80 B) 20 C) 22 D) 44
W ramach wyprzedaży sezonowej płaszcz o początkowej wartości 240 zł przeceniono na 200 zł. Zatem cenę tego płaszcza obniżono o
A) 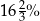 jego początkowej wartości.
jego początkowej wartości.
B) 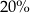 jego początkowej wartości.
jego początkowej wartości.
C) 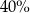 jego początkowej wartości.
jego początkowej wartości.
D) 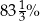 jego początkowej wartości.
jego początkowej wartości.
Rower kosztujący 270 zł sprzedano podczas wyprzedaży za 216 zł. Obniżka wynosiła
A) 15% B) 20% C) 40% D) 80%
Książka kosztowała 75 zł, a po obniżce 60 zł. O ile procent obniżono cenę książki?
A) 20% B) 25% C) 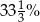 D) 75%
D) 75%
Kurtkę, która kosztowała 450 złotych, przeceniono i sprzedano za 387 złotych. O ile procent obniżono cenę kurtki?
A) 14 B) 15 C) 20 D) 24
Kąty 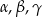 pewnego trójkąta spełniają dwa warunki:
pewnego trójkąta spełniają dwa warunki: 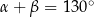 i
i 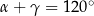 .
.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Kąt  ma miarę ma miarę 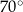 . . | P | F |
Różnica miar między kątem największym a kątem najmniejszym w tym trójkącie jest równa 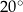 . . | P | F |
Na wykresie przedstawiono, jak zmienia się masa beczki z benzyną w zależności od objętości wlanej do niej benzyny.
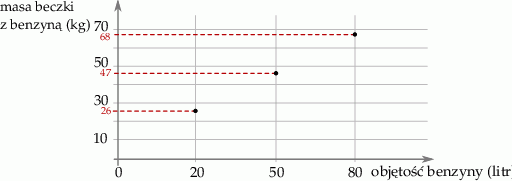
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Beczka, do której nalano 100 litrów benzyny waży 82 kg. | P | F |
| Beczka waży 15 kg. | P | F |
Uczeń pomyślał pewną liczbę. Następnie dodał do niej 5, otrzymaną sumę podzielił przez 3, a otrzymany iloraz pomnożył przez 4. Potem od ostatniego wyniku odjął 6. Gdy tę różnicę podzielił przez 7, to otrzymał liczbę 2. Jaką liczbę pomyślał uczeń?
Dane są cztery liczby całkowite: 1258754, 865422, 5418712, 8530236. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Wśród podanych liczb są 2 liczby podzielne przez 12. | P | F |
| Wśród podanych liczb są 2 liczby podzielne przez 18. | P | F |
Prosta 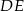 jest równoległa do boku
jest równoległa do boku 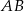 trójkąta
trójkąta 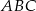 i przecina bok
i przecina bok 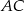 w punkcie
w punkcie 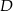 , bok
, bok 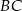 w punkcie
w punkcie 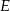 . Oblicz
. Oblicz 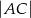 jeśli
jeśli 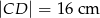 ,
, 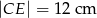 i
i 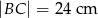 .
.
Prosta 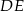 jest równoległa do boku
jest równoległa do boku 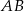 trójkąta
trójkąta 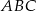 i przecina bok
i przecina bok 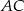 w punkcie
w punkcie 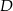 , bok
, bok 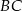 w punkcie
w punkcie 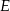 . Oblicz
. Oblicz 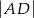 jeśli
jeśli 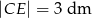 ,
, 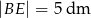 i
i 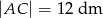 .
.
Prosta 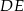 jest równoległa do boku
jest równoległa do boku 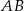 trójkąta
trójkąta 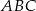 i przecina bok
i przecina bok 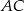 w punkcie
w punkcie 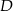 , bok
, bok 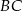 w punkcie
w punkcie 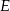 . Oblicz
. Oblicz 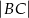 , jeśli
, jeśli 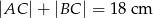 ,
, 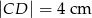 i
i 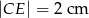 .
.
Funkcja 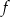 jest określona wzorem
jest określona wzorem 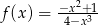 . Wartość tej funkcji dla argumentu równego
. Wartość tej funkcji dla argumentu równego 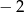 wynosi:
wynosi:
A) 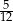 B)
B) 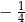 C)
C)  D)
D) 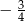
Funkcja 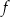 jest określona wzorem
jest określona wzorem 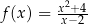 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej 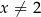 . Wartość funkcji
. Wartość funkcji 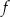 dla argumentu 4 jest równa
dla argumentu 4 jest równa
A) 6 B) 2 C) 10 D) 8
Funkcja 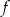 jest określona wzorem
jest określona wzorem 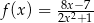 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wartość funkcji
. Wartość funkcji 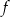 dla argumentu 1 jest równa
dla argumentu 1 jest równa
A) 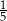 B)
B) 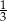 C) 1 D) 2
C) 1 D) 2
Pole powierzchni bocznej graniastosłupa prawidłowego czworokątnego jest 6 razy większe, od jego pola podstawy, a objętość tego graniastosłupa jest równa 12. Oblicz długość krawędzi podstawy oraz długość przekątnej tego graniastosłupa. Zapisz obliczenia.
Na diagramie słupkowym przedstawiono liczby medali zdobytych na czterech letnich igrzyskach olimpijskich przez reprezentację Polski.
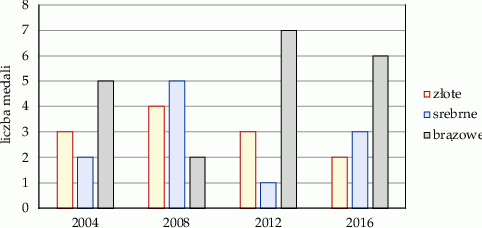
Oceń prawdziwość podanych zdań, dotyczących medali zdobytych przez reprezentację Polski podczas letnich igrzysk olimpijskich w latach 2004–2016. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Liczba zdobytych złotych medali stanowi więcej niż jedną trzecią liczby wszystkich zdobytych medali. | P | F |
| Podczas letnich igrzysk olimpijskich średnio zdobywano 3 złote medale. | P | F |
Na diagramie słupkowym przedstawiono liczby medali zdobytych na czterech letnich igrzyskach olimpijskich przez reprezentację Polski.
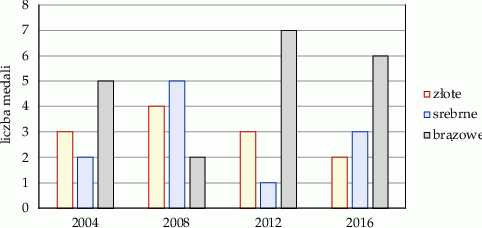
Oceń prawdziwość podanych zdań, dotyczących medali zdobytych przez reprezentację Polski podczas letnich igrzysk olimpijskich w latach 2004–2016. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Na igrzyskach zdobyto więcej medali złotych niż srebrnych. | P | F |
| Podczas letnich igrzysk olimpijskich średnio zdobywano 3 srebrne medale. | P | F |
Kasia ma 6 lat. Średnia arytmetyczna wieku Ani i Pawła jest równa 12 lat. Średnia arytmetyczna wieku Kasi, Ani i Pawła jest równa
A) 6 lat B) 9 lat C) 10 lat D) 15 lat
Ola ma 7 lat. Średnia arytmetyczna wieku Ewy i Karola jest równa 10 lat. Średnia arytmetyczna wieku Oli, Ewy i Karola jest równa
A) 6 lat B) 9 lat C) 10 lat D) 15 lat
Plac ma kształt prostokąta, którego jeden bok jest 4 razy dłuższy od drugiego boku. Wokół placu rośnie pas trawy o szerokości jednego metra. Trawnik otoczono płotem otrzymując prostokąt o obwodzie 48 m. Jakie wymiary ma plac?
Wskaż rysunek, na którym przedstawiono przedział, będący zbiorem wszystkich rozwiązań nierówności 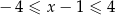 .
.
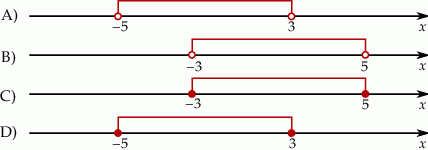
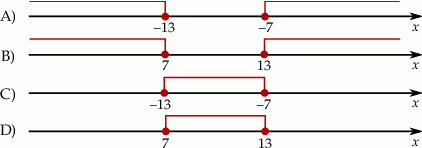
Wskaż rysunek, na którym jest przedstawiony zbiór wszystkich liczb  spełniających warunek:
spełniających warunek: 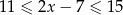 .
.
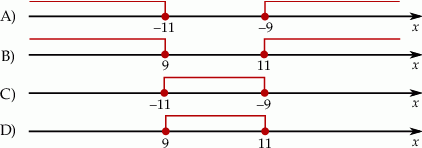
Rozwiązaniem nierówności 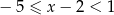 jest zbiór
jest zbiór
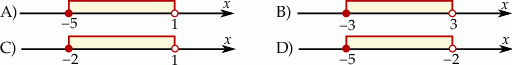
Wskaż rysunek, na którym przedstawiono przedział, będący zbiorem wszystkich rozwiązań nierówności 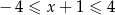 .
.
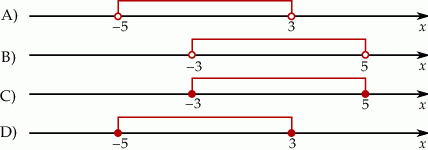
Rozwiązaniem nierówności 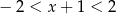 jest zbiór liczb
jest zbiór liczb
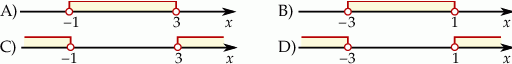
Rozwiązaniem nierówności 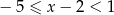 jest zbiór
jest zbiór
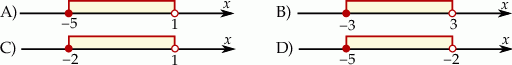
Rozwiązaniem nierówności 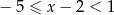 jest zbiór
jest zbiór
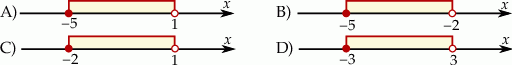
Wskaż rysunek, na którym jest przedstawiony zbiór wszystkich liczb  spełniających warunek:
spełniających warunek: 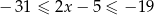 .
.
Maja, Ola i Jagna kupowały zeszyty. Maja za 3 grube zeszyty i 8 cienkich zapłaciła 10 zł. Ola kupiła 4 grube oraz 4 cienkie zeszyty i również zapłaciła 10 zł. Czy Jagnie wystarczy 10 złotych na zakup 5 grubych zeszytów i 1 cienkiego? Zapisz obliczenia i odpowiedź.
Olaf, Kacper i Łukasz kupowali słodycze. Olaf za 10 cukierków czekoladowych i 3 lizaki zapłacił 21 zł. Kacper kupił 6 cukierków czekoladowych i 6 lizaków i również zapłacił 21 zł. Czy Łukaszowi wystarczy 21 złotych na zakup 8 cukierków czekoladowych i 4 lizaków? Zapisz obliczenia i odpowiedź.
Kulki magnetyczne są sprzedawane w zestawach w kształcie sześcianu o krawędzi składającej się z 6 kulek (zobacz rysunek).

Kamil kupił 3 takie zestawy kulek magnetycznych, a następnie zbudował z nich wszystkich pewną liczbę sześcianów o krawędzi składającej się z 3 kulek.
Kamil kupił w sumie A/B kulek magnetycznych.
A) 648 B) 216
Kamil zbudował C/D sześciany o krawędzi składającej się z 3 kulek.
C) 24 D) 72
Suma liczby  i
i 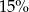 tej liczby jest równa 230. Równaniem opisującym tę zależność jest
tej liczby jest równa 230. Równaniem opisującym tę zależność jest
A) 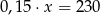 B)
B) 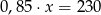 C)
C) 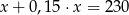 D)
D) 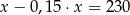
Różnica liczby  i
i 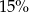 tej liczby jest równa 255. Równaniem opisującym tę zależność jest
tej liczby jest równa 255. Równaniem opisującym tę zależność jest
A) 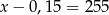 B)
B) 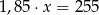 C)
C) 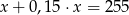 D)
D) 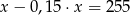
Cztery pompy o jednakowej wydajności pracując jednocześnie, wypompowały wodę zgromadzoną w zbiorniku w czasie 12 godzin.
Ile takich pomp należałoby użyć, aby tę samą ilość wody wypompować w ciągu 6 godzin?
A) 2 B) 3 C) 6 D) 8
Trzy pompy o jednakowej wydajności pracując jednocześnie, wypompowały wodę zgromadzoną w zbiorniku w czasie 24 godzin.
Ile takich pomp należałoby użyć, aby tę samą ilość wody wypompować w ciągu 8 godzin?
A) 9 B) 8 C) 6 D) 12
Starożytne rury były wykonane z materiału, który nieomal w całości składał się z czystego ołowiu. Jedynie 9% tego materiału stanowiły zanieczyszczenia. Ile kilogramów czystego ołowiu zawierała rura o wadze 80 kilogramów?
Na rysunku przedstawiono prostokąt. Długość dłuższego boku oznaczono symbolem  oraz opisano za pomocą wyrażenia algebraicznego
oraz opisano za pomocą wyrażenia algebraicznego 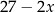 . Długość krótszego boku oznaczono symbolem
. Długość krótszego boku oznaczono symbolem 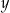 oraz opisano za pomocą wyrażenia algebraicznego
oraz opisano za pomocą wyrażenia algebraicznego 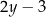 .
.
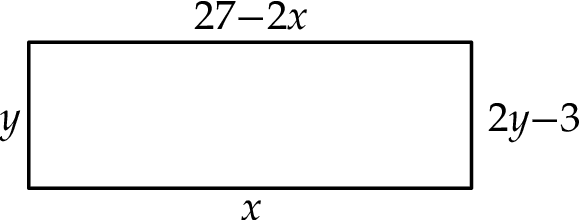
Które równanie nie opisuje poprawnej zależności między wartościami  i
i 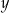 ?
?
A) 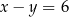 B)
B) 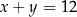 C)
C) 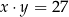 D)
D) 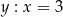
Na rysunku przedstawiono prostokąt. Długość dłuższego boku oznaczono symbolem  oraz opisano za pomocą wyrażenia algebraicznego
oraz opisano za pomocą wyrażenia algebraicznego 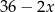 . Długość krótszego boku oznaczono symbolem
. Długość krótszego boku oznaczono symbolem 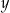 oraz opisano za pomocą wyrażenia algebraicznego
oraz opisano za pomocą wyrażenia algebraicznego 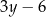 .
.
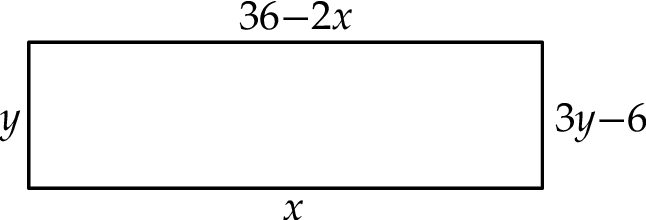
Które równanie nie opisuje poprawnej zależności między wartościami  i
i 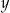 ?
?
A) 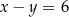 B)
B) 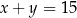 C)
C) 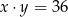 D)
D)