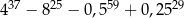Dane są dwie liczby
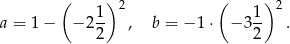
Wartość wyrażenia 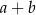 jest równa A/B.
jest równa A/B.
A) 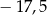 B) 18,5
B) 18,5
Wartość wyrażenia 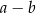 jest równa C/D.
jest równa C/D.
C) 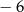 D) 7
D) 7
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Dane są dwie liczby
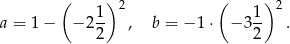
Wartość wyrażenia 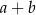 jest równa A/B.
jest równa A/B.
A) 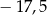 B) 18,5
B) 18,5
Wartość wyrażenia 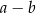 jest równa C/D.
jest równa C/D.
C) 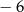 D) 7
D) 7
Okrąg o środku w punkcie 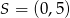 ma promień długości 1 i jest styczny do okręgu o środku
ma promień długości 1 i jest styczny do okręgu o środku 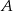 i promieniu długości 10. Punkt
i promieniu długości 10. Punkt 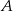 leży na osi
leży na osi 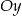 . Jakie ma współrzędne?
. Jakie ma współrzędne?
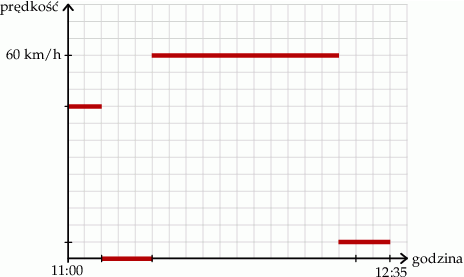
Mateusz mieszka w odległości 4 km od szkoły. Część drogi do szkoły pokonuje pieszo, idąc do przystanku autobusowego. Tam czeka na autobus, a następnie wsiada do niego i jedzie do szkoły. Pewnego dnia, gdy był już na przystanku, stwierdził, że zapomniał zabrać zeszyt, więc wrócił po niego do domu. Wykres przedstawia, jak tego dnia zmieniała się odległość Mateusza od domu w zależności od czasu.
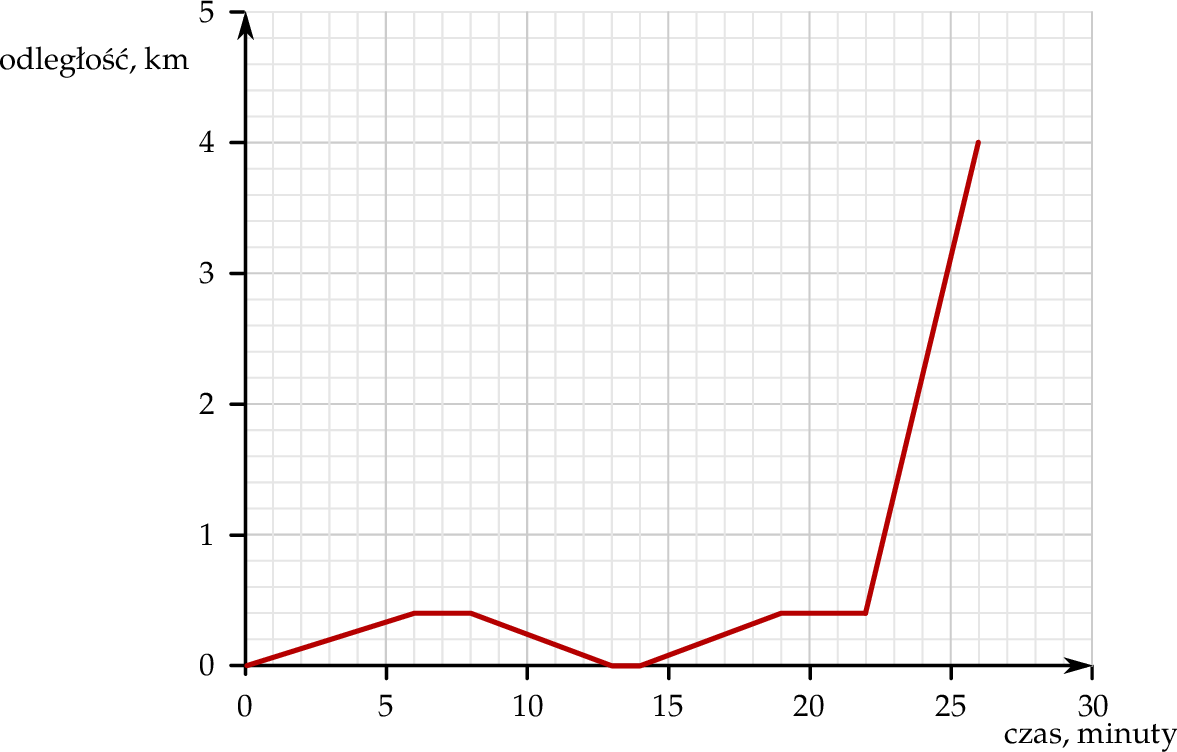
Od momentu, gdy Mateusz zawrócił z przystanku do domu, do momentu, gdy dotarł ponownie na przystanek, upłynęło
A) 11 minut. B) 13 minut. C) 14 minut. D) 16 minut.
Mateusz mieszka w odległości 4 km od szkoły. Część drogi do szkoły pokonuje pieszo, idąc do przystanku autobusowego. Tam czeka na autobus, a następnie wsiada do niego i jedzie do szkoły. Pewnego dnia, gdy był już na przystanku, stwierdził, że zapomniał zabrać zeszyt, więc wrócił po niego do domu. Wykres przedstawia, jak tego dnia zmieniała się odległość Mateusza od domu w zależności od czasu.
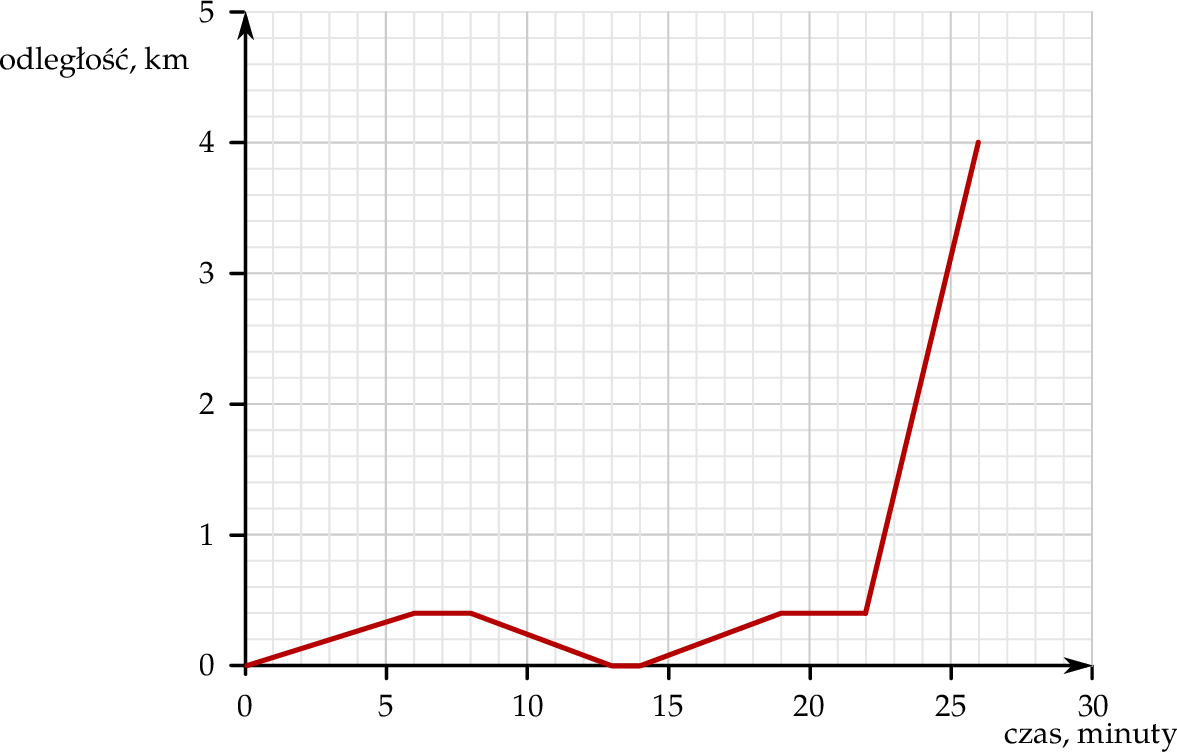
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Dom Mateusza znajduje się w odległości 400 m od przystanku autobusowego. | P | F |
Autobus drogę między przystankami pokonał z prędkością 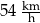 . . | P | F |
Rozwiązaniem równania 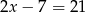 jest liczba
jest liczba
A) 7 B) 14 C) 26 D) 28
Miejscowości 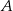 i
i 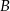 położone na przeciwległych brzegach jeziora są połączone dwiema drogami – drogą polną prowadzącą przez punkt
położone na przeciwległych brzegach jeziora są połączone dwiema drogami – drogą polną prowadzącą przez punkt 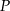 i drogą leśną prowadzącą przez punkt
i drogą leśną prowadzącą przez punkt 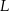 . Długość drogi polnej
. Długość drogi polnej 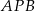 wynosi 10 km, a długość drogi leśnej
wynosi 10 km, a długość drogi leśnej 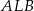 jest równa 6 km.
jest równa 6 km.
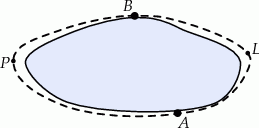
Matylda i Karol wyruszyli na rowerach z miejscowości 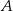 do miejscowości
do miejscowości 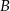 o godzinie 10:00. Matylda jechała drogą leśną, a Karol – drogą polną. Średnia prędkość jazdy Matyldy wynosiła
o godzinie 10:00. Matylda jechała drogą leśną, a Karol – drogą polną. Średnia prędkość jazdy Matyldy wynosiła 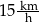 , a średnia prędkość Karola była równa
, a średnia prędkość Karola była równa 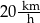 .
.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Do miejscowości 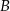 Karol przyjechał wcześniej niż Matylda. Karol przyjechał wcześniej niż Matylda. | P | F |
Matylda przyjechała do miejscowości 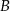 o godzinie 10:24. o godzinie 10:24. | P | F |
Marta zapisała w systemie rzymskim cztery liczby: CLXX, CXC, CCLXX oraz CCL. Która z nich znajduje się na osi liczbowej najbliżej liczby 200?
A) CLXX B) CXC C) CCLXX D) CCL
Zapisz w jak najprostszej postaci 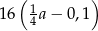 .
.
Zapisz w jak najprostszej postaci 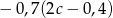 .
.
Zapisz w jak najprostszej postaci 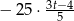 .
.
Zapisz w jak najprostszej postaci 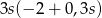 .
.
Zapisz w jak najprostszej postaci 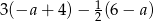 .
.
Zapisz w jak najprostszej postaci 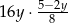 .
.
Zapisz w jak najprostszej postaci 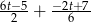 .
.
Zapisz w jak najprostszej postaci 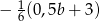 .
.
Zapisz w jak najprostszej postaci 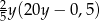 .
.
Zapisz w jak najprostszej postaci 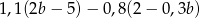 .
.
Zapisz w jak najprostszej postaci 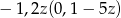 .
.
Zmieszano 100 litrów mleka 2% i 25 litrów mleka 4%. Otrzymano mleko, które ma w sobie 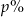 tłuszczu. Wynika stąd, że
tłuszczu. Wynika stąd, że
A) 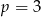 B)
B) 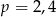 C)
C) 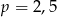 D)
D) 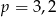
Zmieszano 60 litrów mleka 2,5% i 40 litrów mleka 3%. Otrzymano mleko, które ma w sobie 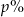 tłuszczu. Wynika stąd, że
tłuszczu. Wynika stąd, że
A) 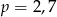 B)
B) 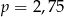 C)
C) 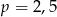 D)
D) 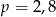
Zmieszano 15 g 20% roztworu z 25 g 12% roztworu. Stężenie procentowe otrzymanego roztworu jest równe
A) 15% B) 14% C) 16% D) 18%
Zmieszano 2,5 szklanki octu 6% z 1,5 szklanki octu 10%. Jakie jest stężenie otrzymanej mieszanki?
A) 9% B) 8% C) 7% D) 7,5%
Zmieszano 25 litrów mleka 2% i 100 litrów mleka 4%. Otrzymano mleko, które ma w sobie 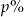 tłuszczu. Wynika stąd, że
tłuszczu. Wynika stąd, że
A) 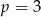 B)
B) 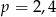 C)
C) 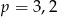 D)
D) 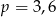
O liczbach 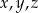 wiemy, że kwadrat ich iloczynu jest o 20% większy od odwrotności ich sumy. Która równość poprawnie opisuje zależność wiążącą liczby
wiemy, że kwadrat ich iloczynu jest o 20% większy od odwrotności ich sumy. Która równość poprawnie opisuje zależność wiążącą liczby 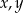 i
i  ?
?
A) 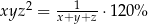 B)
B) 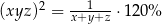
C) 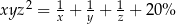 D)
D) 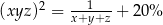
Na kartce w kratkę Tomek narysował według pewnej reguły cztery łamane (patrz rysunek).
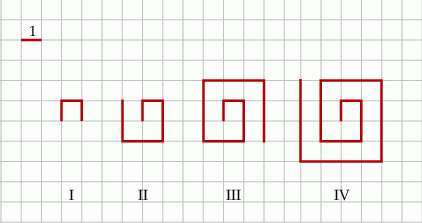
Długości tych łamanych zapisał w tabeli.
| Numer łamanej | I | II | III | IV |
| Długość łamanej | 3 | 8 | 15 | 24 |
Kolejne łamane – od numeru V – Tomek rysował zgodnie z tą samą regułą.
Łamana o długości 48 ma numer A/B.
A) VI B) VII
Łamana o numerze VIII ma długość C/D.
C) 63 D) 80
Na kartce w kratkę Tomek narysował według pewnej reguły cztery łamane (patrz rysunek).
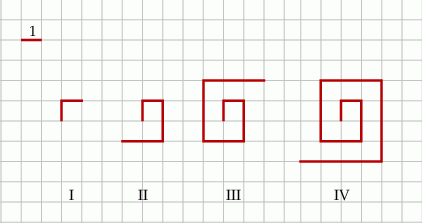
Długości tych łamanych zapisał w tabeli.
| Numer łamanej | I | II | III | IV |
| Długość łamanej | 2 | 6 | 12 | 20 |
Kolejne łamane – od numeru V – Tomek rysował zgodnie z tą samą regułą.
Łamana o długości 56 ma numer A/B.
A) VI B) VII
Łamana o numerze VIII ma długość C/D.
C) 72 D) 80
W trójkącie 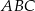 dwusieczna kąta przy wierzchołku
dwusieczna kąta przy wierzchołku 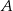 przecina symetralną boku
przecina symetralną boku 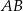 pod kątem
pod kątem 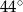 . Uzasadnij, że trójkąt
. Uzasadnij, że trójkąt 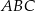 jest trójkątem rozwartokątnym.
jest trójkątem rozwartokątnym.
Proste 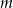 i
i  są styczne do okręgu i przecinają się pod kątem
są styczne do okręgu i przecinają się pod kątem 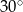 .
.
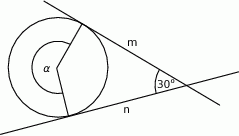
Miara kąta  jest równa
jest równa
A) 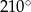 B)
B) 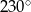 C)
C) 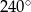 D)
D) 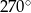
Proste 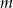 i
i  są styczne do okręgu i przecinają się pod kątem
są styczne do okręgu i przecinają się pod kątem 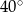 .
.
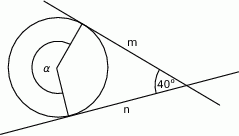
Miara kąta  jest równa
jest równa
A) 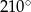 B)
B) 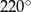 C)
C) 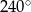 D)
D) 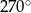
Ania pomyślała o pewnej liczbie dodatniej. Dodała do niej 96 i wynik potroiła. Okazało się, że otrzymana w ten sposób liczba jest o 400% większa od liczby, o której pomyślała Ania. O jakiej liczbie pomyślała Ania?
A) 72 B) 288 C) 144 D) 48
Oblicz pole sześciokąta foremnego o boku długości 2.
Zmieszano 40 dag rodzynek w cenie 12 zł za kilogram oraz 60 dag pestek dyni w cenie 17 zł za kilogram. Ile kosztuje 1 kilogram tej mieszanki?
Pudełko w kształcie prostopadłościanu o wymiarach przedstawionych na rysunku zawiera 32 czekoladki. Każda czekoladka ma kształt prostopadłościanu o wymiarach 2 cm, 2 cm i 1,5 cm. Ile procent objętości pudełka stanowi objętość wszystkich czekoladek?
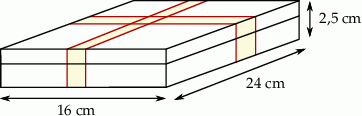
Hugo wybrał się do kolegi mieszkającego w Tczewie. Tata podwiózł go na przystanek pociągu, potem Hugo czekał na przyjazd pociągu. Po przyjeździe do Tczewa, Hugo doszedł pieszo do mieszkania kolegi. Na wykresie w sposób uproszczony przedstawiono zależność prędkości, z jaką poruszał się Hugo, od czasu.
Oblicz długość trasy pokonanej przez Huga od wyjścia z domu do chwili dotarcia do mieszkania kolegi.
Ile spośród punktów: 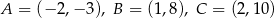 należy do wykresu funkcji
należy do wykresu funkcji 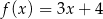 ?
?
A) nie należy żaden B) należy tylko jeden
C) należą tylko dwa D) należą wszystkie trzy
Ile spośród punktów: 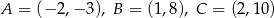 należy do wykresu funkcji
należy do wykresu funkcji 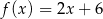 ?
?
A) nie należy żaden B) należy tylko jeden
C) należą tylko dwa D) należą wszystkie trzy
Ile spośród punktów: 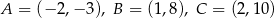 należy do wykresu funkcji
należy do wykresu funkcji 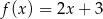 ?
?
A) nie należy żaden B) należy tylko jeden
C) należą tylko dwa D) należą wszystkie trzy
Liczba 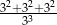 jest równa
jest równa
A) 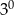 B)
B) 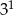 C)
C) 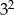 D)
D) 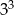
Liczba 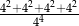 jest równa
jest równa
A) 1 B) 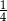 C) 4 D)
C) 4 D) 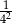
Liczba 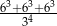 jest równa
jest równa
A) 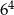 B)
B) 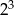 C)
C) 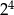 D)
D) 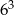
Liczba 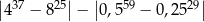 jest równa
jest równa
A) 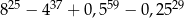 B)
B) 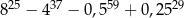
C) 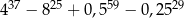 D)
D)