Pewnego dnia w klasie Ib było dwa razy więcej uczniów, niż w klasie Ia. Tego samego dnia dziewczynki stanowiły 60% uczniów klasy Ia, oraz 40% uczniów klasy Ib. Jeżeli tego dnia wylosujemy jednego ucznia z klas Ia i Ib, to prawdopodobieństwo wylosowania chłopca jest równe
A) 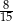 B)
B) 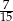 C)
C) 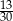 D)
D) 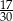
/Szkoła podstawowa
Pewnego dnia w klasie Ib było dwa razy więcej uczniów, niż w klasie Ia. Tego samego dnia dziewczynki stanowiły 40% uczniów klasy Ia, oraz 60% uczniów klasy Ib. Jeżeli tego dnia wylosujemy jednego ucznia z klas Ia i Ib, to prawdopodobieństwo wylosowania chłopca jest równe
A) 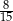 B)
B) 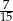 C)
C) 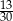 D)
D) 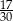
Fosfor stanowi 0,5% masy kaszy gryczanej.
- Ile gramów fosforu zawiera 150-gramowa porcja kaszy?
- Jaka porcja kaszy zawiera 2 g fosforu?
Ania i Tomek mają razem 14 lat. Dwa lata temu Tomek był 4 razy starszy od Ani.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Ania jest dwa razy młodsza od Tomka. | P | F |
| Tomek jest o 6 lat starszy od Ani. | P | F |
Stężenie roztworu kwasu siarkowego przez pierwszą godzinę pewnego eksperymentu było równe 25%. Na początku drugiej godziny eksperymentu stężenie zmalało o 5 punktów procentowych. Oznacza to, że stężenie tego roztworu kwasu siarkowego zmalało o
A) 5% B) 25% C) 20% D) 75%
Przekrój osiowy stożka jest trójkątem równobocznym o boku długości 6.
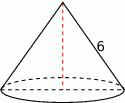
Pole powierzchni bocznej tego stożka jest równe
A) 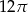 B)
B) 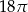 C)
C) 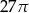 D)
D) 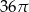
Przekrój osiowy stożka jest trójkątem równobocznym o boku długości 4.
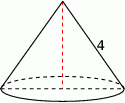
Pole powierzchni bocznej tego stożka jest równe
A) 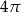 B)
B) 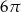 C)
C) 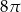 D)
D) 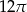
Pole powierzchni bocznej stożka o kącie rozwarcia 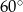 i promieniu podstawy 3 cm jest równe
i promieniu podstawy 3 cm jest równe
A) 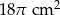 B)
B) 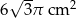 C)
C) 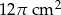 D)
D) 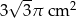
Przekrój osiowy stożka jest trójkątem równobocznym o boku długości 8.
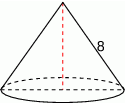
Pole powierzchni bocznej tego stożka jest równe
A) 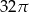 B)
B) 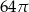 C)
C) 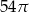 D)
D) 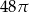
Wykres funkcji liniowej 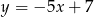 przecina pionową prostą przechodzącą przez punkt
przecina pionową prostą przechodzącą przez punkt 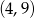 w punkcie o współrzędnych
w punkcie o współrzędnych
A) 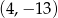 B)
B) 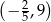 C)
C) 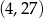 D)
D) 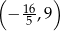
Wykres funkcji liniowej 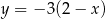 przecina prostą
przecina prostą 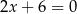 w punkcie
w punkcie
A) 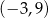 B)
B) 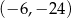 C)
C) 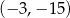 D)
D) 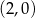
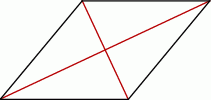
Jeżeli 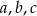 i
i 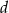 są długościami kolejnych boków czworokąta, to przekątne tego czworokąta są prostopadłe wtedy i tylko wtedy, gdy
są długościami kolejnych boków czworokąta, to przekątne tego czworokąta są prostopadłe wtedy i tylko wtedy, gdy 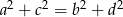 . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Czworokąt, którego dwa przeciwległe boki mają długości 7 i 24, a dwa pozostałe boki mają długości 15 i 20 ma prostopadłe przekątne. | P | F |
Czworokąt, w którym długości kolejnych boków są równe: 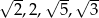 ma prostopadłe przekątne. ma prostopadłe przekątne. | P | F |
Jeżeli 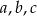 i
i 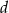 są długościami kolejnych boków czworokąta, to przekątne tego czworokąta są prostopadłe wtedy i tylko wtedy, gdy
są długościami kolejnych boków czworokąta, to przekątne tego czworokąta są prostopadłe wtedy i tylko wtedy, gdy 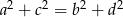 . Jeżeli trzy kolejne boki czworokąta mają długości: 5, 6, 7 oraz przekątne tego czworokąta są prostopadłe, to czwarty bok tego czworokąta ma długość
. Jeżeli trzy kolejne boki czworokąta mają długości: 5, 6, 7 oraz przekątne tego czworokąta są prostopadłe, to czwarty bok tego czworokąta ma długość
A) 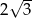 B)
B) 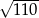 C)
C) 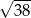 D)
D) 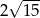
Dane są liczby 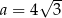 ,
, 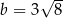 ,
, 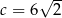 ,
, 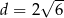 . Która zależność jest prawdziwa?
. Która zależność jest prawdziwa?
A) 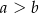 B)
B) 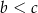 C)
C) 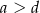 D)
D) 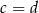
Jeżeli uczniów klasy IIb ustawi się trójkami, a uczniów klasy IIc ustawi się parami, to liczba par jest o 3 większa niż liczba trójek. Jeżeli natomiast uczniów klasy IIb ustawi się w parach, a uczniów klasy IIc ustawi się trójkami, to jeden uczeń klasy IIb pozostanie bez pary, a liczba par będzie o 5 większa niż liczba trójek. Ilu uczniów jest w klasach IIb i IIc? Zapisz obliczenia.
Różnica miar dwóch przeciwległych kątów deltoidu jest równa 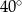 . Suma miar dwóch sąsiednich kątów tego deltoidu może być równa
. Suma miar dwóch sąsiednich kątów tego deltoidu może być równa
A) 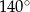 B)
B) 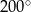 C)
C) 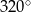 D)
D) 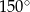
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
15 minut to 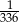 tygodnia. tygodnia. | P | F |
12 sekund to 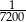 doby. doby. | P | F |
Zależność między miarą kąta wewnętrznego (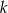 ) a liczbą boków (
) a liczbą boków ( ) wielokąta foremnego określa wzór
) wielokąta foremnego określa wzór 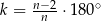 . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Miara kąta wewnętrznego w 24–kącie wypukłym jest o 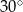 większa od miary kąta wewnętrznego ośmiokąta foremnego. większa od miary kąta wewnętrznego ośmiokąta foremnego. | P | F |
Jeżeli miara kąta wewnętrznego wielokąta foremnego jest równa 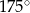 , to wielokąt ten ma 60 boków. , to wielokąt ten ma 60 boków. | P | F |
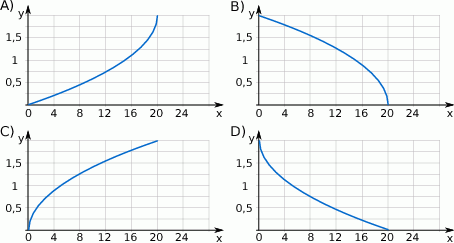
Piłkę tenisową puszczono swobodnie z pewnej wysokości. Wzór 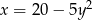 opisuje zależność wysokości
opisuje zależność wysokości  (w metrach) na jakiej znajduje się piłka od czasu
(w metrach) na jakiej znajduje się piłka od czasu 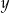 (w sekundach), który upłynął od momentu puszczenia piłki. Który wykres przedstawia tę zależność?
(w sekundach), który upłynął od momentu puszczenia piłki. Który wykres przedstawia tę zależność?
Pole rombu jest równe 36, a jedna z jego przekątnych jest dwa razy krótsza od drugiej.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Kąt ostry rombu ma miarę 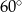 | P | F |
Bok rombu ma długość 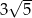 . . | P | F |
Cena brutto = cena netto + podatek VAT
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Jeżeli cena netto 1 kg gruszek wzrośnie o 100%, to cena bruttoteż wzrośnie o 100%. | P | F |
| Jeżeli cena netto książki wzrośnie o 20 zł, to cena książki z 5% podatkiem VAT wzrośnie o 21 zł. | P | F |
W poniedziałek pan Ryszard, mieszkaniec wsi Janki, odwiózł córkę do szkoły w Gródku, a następnie pojechał na kontrolę swoich sklepów w Sowach i w Migocku. Na schematycznej mapce przedstawiono drogi łączące te miejscowości, a na wykresie – jak zmieniała się w czasie tej podróży odległość (mierzona w linii prostej) pana Ryszarda od domu.
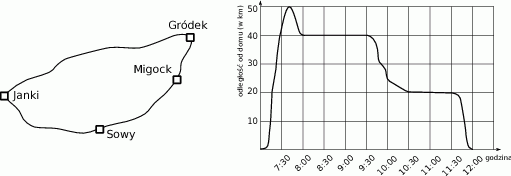
Jaka jest odległość (w linii prostej) między Jankami a Gródkiem?
A) 50 km B) 40 km C) 20 km D) 10 km
W poniedziałek pan Ryszard, mieszkaniec wsi Janki, odwiózł córkę do szkoły w Gródku, a następnie pojechał na kontrolę swoich sklepów w Sowach i w Migocku. Na schematycznej mapce przedstawiono drogi łączące te miejscowości, a na wykresie – jak zmieniała się w czasie tej podróży odległość (mierzona w linii prostej) pana Ryszarda od domu.
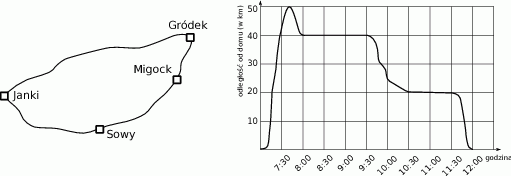
Z podanych informacji wynika, że pan Ryszard
A) najpierw kontrolował sklep w Sowach.
B) między Sowami a Migockiem zatrzymał się na 15 minut.
C) wrócił do domu po 4 godzinach.
D) kontrolował sklep w Sowach co najwyżej godzinę.
Oblicz obwód trójkąta o wierzchołkach: 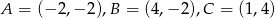 .
.
Oblicz obwód trójkąta o wierzchołkach: 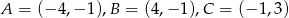 .
.
Dany jest trapez prostokątny 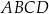 , w którym
, w którym 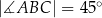 . Punkty
. Punkty 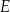 i
i 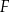 są środkami odpowiednio odcinków
są środkami odpowiednio odcinków 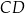 i
i 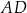 .
.

Długość odcinka 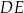 jest równa 6, a długość odcinka
jest równa 6, a długość odcinka 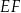 jest równa 10. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
jest równa 10. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Obwód trapezu  jest liczbą całkowitą. jest liczbą całkowitą. | P | F |
Pole trapezu  jest równe 320. jest równe 320. | P | F |
Wartość wyrażenia 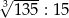 jest równa wartości wyrażenia A/B.
jest równa wartości wyrażenia A/B.
A) 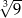 B)
B) 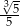
Wartość wyrażenia 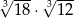 jest równa wartości wyrażenia C/D.
jest równa wartości wyrażenia C/D.
C) 6 D) 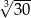
Wartość wyrażenia 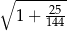 jest równa A/B.
jest równa A/B.
A) 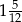 B)
B) 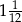
Wartość wyrażenia 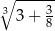 jest równa C/D.
jest równa C/D.
C) 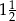 D)
D) 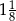
Wartość wyrażenia 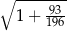 jest równa A/B.
jest równa A/B.
A) 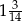 B)
B) 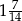
Wartość wyrażenia 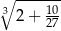 jest równa C/D.
jest równa C/D.
C) 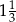 D)
D) 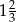
Na diagramie przedstawiono rozkład liczby punktów zdobytych przez zawodników biorących udział w grze Kulki.
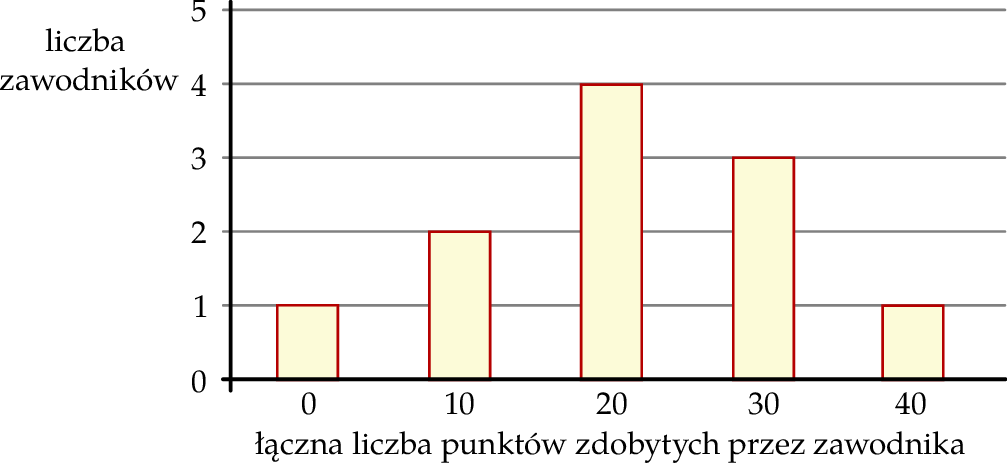
Oblicz prawdopodobieństwo, że losowo wybrany zawodnik zdobył w tej grze więcej niż 20 punktów.

