Każdą z dwóch identycznych prostokątnych kartek papieru rozcięto na dwie części. Z pierwszej kartki otrzymano dwa prostokąty o obwodach 40 cm każdy, z drugiej zaś również dwa prostokąty, ale o obwodach 50 cm każdy. Oblicz obwód wyjściowych kartek.
A) 40 cm B) 50 cm C) 60 cm D) 80 cm E) 90 cm
/Konkursy/Zadania testowe/Geometria/Planimetria/Czworokąty
Kwadrat o polu 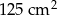 podzielono na pięć części o równych polach. Cztery z nich to kwadraty, a piąta to sześciokąt w kształcie litery L. Jaka jest długość najkrótszego boku tego sześciokąta?
podzielono na pięć części o równych polach. Cztery z nich to kwadraty, a piąta to sześciokąt w kształcie litery L. Jaka jest długość najkrótszego boku tego sześciokąta?

A) 1 cm B) 1,2 cm C) 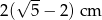 D)
D) 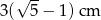 E)
E) 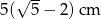
Prostokąt na rysunku tworzy sześć kwadratów. Długość boku najmniejszego kwadratu jest równa 1. Jaką długość ma bok największego kwadratu.
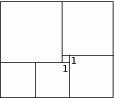
A) 4 B) 5 C) 6 D) 7 E) 8
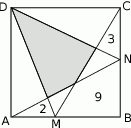
Dany jest kwadrat 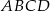 . Odcinki poprowadzone z punktów
. Odcinki poprowadzone z punktów 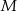 i
i 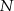 do jego wierzchołków dzielą go na osiem części. Na rysunku zaznaczono pola trzech z nich. Jakie jest pole zacieniowanej części?
do jego wierzchołków dzielą go na osiem części. Na rysunku zaznaczono pola trzech z nich. Jakie jest pole zacieniowanej części?
A) 14 B) 18 C) 11 D) 12 E) 9
Na rysunku obok mały kwadrat wpisano w duży kwadrat. Pole małego kwadratu jest równe
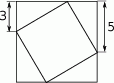
A) 16 B) 28 C) 34 D) 36 E) 49
Okrąg przecina boki prostokąta  w punktach
w punktach  , jak na rysunku obok. Wiadomo, że
, jak na rysunku obok. Wiadomo, że 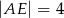 ,
, 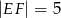 ,
, 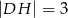 . Ile wynosi długość odcinka
. Ile wynosi długość odcinka 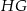 ?
?
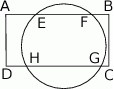
A) 6 B) 7 C) 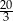 D) 8 E) 9
D) 8 E) 9
Kwadraty przedstawione na rysunku mają boki równe 1. Pole zacieniowanego czworokąta jest równe
A) 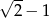 B)
B) 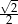 C)
C) 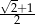 D)
D) 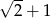 E)
E) 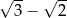
Duży kwadrat o polu 1 został podzielony na kwadraty, jak na rysunku obok. Pole małego zacieniowanego kwadratu jest równe.

A) 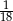 B)
B) 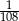 C)
C) 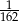 D)
D) 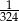 E)
E) 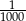
Ile wynosi miara kąta ostrego w rombie, w którym długość boku jest równa średniej geometrycznej długości obu przekątnych?
A) 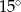 B)
B) 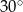 C)
C) 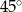 D)
D) 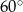 E)
E) 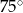
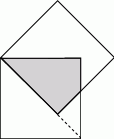
Z punktu 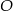 będącego środkiem kwadratu
będącego środkiem kwadratu 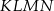 (patrz rysunek) prowadzimy odcinki
(patrz rysunek) prowadzimy odcinki 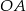 ,
, 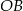 ,
, 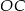 i
i 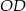 do boków tak, że
do boków tak, że 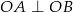 i
i 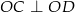 . Ile jest równe pole zacieniowanej części kwadratu, jeśli bok kwadratu ma długość 2?
. Ile jest równe pole zacieniowanej części kwadratu, jeśli bok kwadratu ma długość 2?
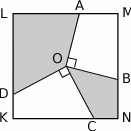
A) 1 B) 2 C) 2,5 D) 2,25 E) zależy od wyboru punktów B i C
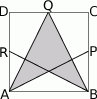
Niech 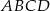 będzie kwadratem o boku 12 cm. Punkty
będzie kwadratem o boku 12 cm. Punkty 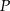 ,
, 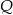 ,
, 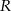 są odpowiednio środkami boków
są odpowiednio środkami boków 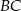 ,
,  ,
,  (rysunek obok). Pole zacieniowanego czworokąta jest równe
(rysunek obok). Pole zacieniowanego czworokąta jest równe
A)  B)
B) 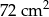 C)
C) 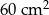 D)
D) 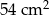 E)
E) 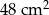
W czworokącie 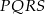 mamy
mamy 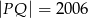 ,
, 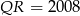 ,
, 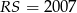 ,
, 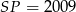 . Przy których wierzchołkach kąty wewnętrzne czworokąta mają zawsze miarę mniejszą niż
. Przy których wierzchołkach kąty wewnętrzne czworokąta mają zawsze miarę mniejszą niż 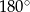 ?
?
A) 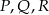 B)
B) 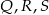 C)
C) 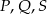 D)
D) 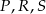 E)
E) 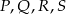
Prostokąt, który widzimy obok na rysunku, podzielono na 7 kwadratów. Bok każdego z zacieniowanych kwadratów ma długość 8. Jaką długość ma bok dużego białego kwadratu?

A) 16 B) 18 C) 20 D) 24 E) 30
Na płaszczyźnie dany jest kwadrat 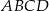 o boku długości 1. Rozważamy wszystkie kwadraty, które mają przynajmniej dwa wierzchołki wspólne z kwadratem
o boku długości 1. Rozważamy wszystkie kwadraty, które mają przynajmniej dwa wierzchołki wspólne z kwadratem 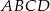 . Jakie jest pole obszaru pokrytego przez te kwadraty?
. Jakie jest pole obszaru pokrytego przez te kwadraty?
A) 5 B) 6 C) 7 D) 8 E) 9
Na rysunku obok przedstawiony jest kwadrat 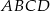 o boku długości 1 oraz łuki okręgów o środkach
o boku długości 1 oraz łuki okręgów o środkach 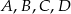 .
.
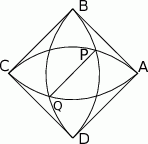
Ile wynosi długość odcinka 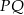 ?
?
A) 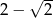 B)
B)  C)
C) 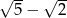 D)
D) 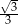 E)
E) 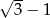
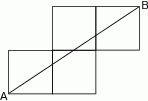
Każdy z czterech kwadratów na rysunku ma bok długości 1. Jaka jest długość odcinka 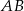 ?
?
A) 5 B) 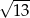 C)
C) 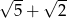 D)
D) 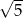 E) Inna odpowiedź
E) Inna odpowiedź
Kwadrat podzielono na 2009 kwadratów, których długości boków są liczbami całkowitymi. Jaką najmniejszą długość może mieć bok dzielonego kwadratu?
A) 44
B) 45
C) 46
D) 503
E) Nie można kwadratu podzielić na 2009 takich kwadratów.

