Dane są dwa przeciwległe wierzchołki kwadratu 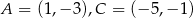 . Wyznacz obwód tego kwadratu.
. Wyznacz obwód tego kwadratu.
/Szkoła średnia/Geometria/Geometria analityczna/Czworokąt
Dane są dwa przeciwległe wierzchołki kwadratu 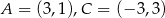 . Oblicz obwód tego kwadratu.
. Oblicz obwód tego kwadratu.
Punkty 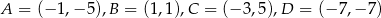 są wierzchołkami trapezu. Oblicz długość krótszej przekątnej tego trapezu.
są wierzchołkami trapezu. Oblicz długość krótszej przekątnej tego trapezu.
Punkty 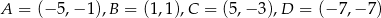 są wierzchołkami trapezu. Oblicz długość krótszej przekątnej tego trapezu.
są wierzchołkami trapezu. Oblicz długość krótszej przekątnej tego trapezu.
Współrzędne przeciwległych wierzchołków prostokąta 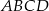 są równe
są równe 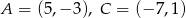 . Wyznacz współrzędne pozostałych wierzchołków prostokąta wiedząc, że wierzchołek
. Wyznacz współrzędne pozostałych wierzchołków prostokąta wiedząc, że wierzchołek 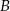 leży na prostej
leży na prostej 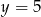 .
.
Punkty 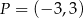 ,
, 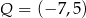 i
i 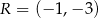 są środkami odpowiednio boków
są środkami odpowiednio boków 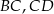 i
i 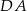 równoległoboku
równoległoboku 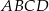 . Wyznacz współrzędne wierzchołków tego równoległoboku.
. Wyznacz współrzędne wierzchołków tego równoległoboku.
Wierzchołkami kwadratu 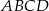 są punkty o współrzędnych
są punkty o współrzędnych 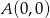 ,
, 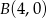 ,
, 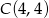 i
i 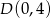 . Dla każdej liczby rzczywistej
. Dla każdej liczby rzczywistej 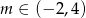 rozważamy trójkąt o wierzchołkach
rozważamy trójkąt o wierzchołkach 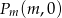 ,
, 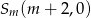 i
i 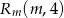 . Wyznacz wszystkie wartości prametru
. Wyznacz wszystkie wartości prametru 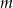 , dla których pole figury, która jest częścią wspólną kwadratu
, dla których pole figury, która jest częścią wspólną kwadratu 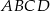 i trójkąta
i trójkąta 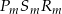 wynosi 2.
wynosi 2.
Dane są współrzędne dwóch kolejnych wierzchołków kwadratu 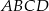 :
: 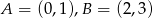 . Wyznacz współrzędne wierzchołka
. Wyznacz współrzędne wierzchołka 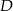 , jeśli wiesz, że kwadrat jest zawarty w I i II ćwiartce układu współrzędnych.
, jeśli wiesz, że kwadrat jest zawarty w I i II ćwiartce układu współrzędnych.
Boki 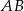 i
i 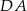 rombu
rombu 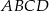 są zawarte odpowiednio w prostych o równaniach
są zawarte odpowiednio w prostych o równaniach 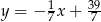 i
i 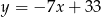 . Napisz równanie prostej zawierającej przekątną
. Napisz równanie prostej zawierającej przekątną 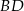 tego rombu, jeżeli jego środek ma współrzędne
tego rombu, jeżeli jego środek ma współrzędne 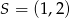 .
.
Dany jest kwadrat 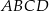 , w którym
, w którym 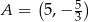 . Przekątna
. Przekątna 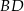 tego kwadratu jest zawarta w prostej o równaniu
tego kwadratu jest zawarta w prostej o równaniu 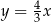 . Oblicz współrzędne punktu przecięcia przekątnych
. Oblicz współrzędne punktu przecięcia przekątnych 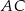 i
i 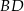 oraz pole kwadratu
oraz pole kwadratu 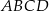 .
.
Dany jest kwadrat 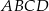 , w którym
, w którym 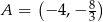 . Przekątna
. Przekątna 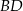 tego kwadratu jest zawarta w prostej o równaniu
tego kwadratu jest zawarta w prostej o równaniu 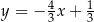 . Oblicz współrzędne punktu przecięcia przekątnych
. Oblicz współrzędne punktu przecięcia przekątnych 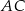 i
i 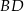 oraz pole kwadratu
oraz pole kwadratu 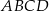 .
.
Przekątna 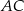 rombu
rombu 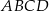 jest zawarta w prostej o równaniu
jest zawarta w prostej o równaniu 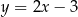 . Wierzchołki
. Wierzchołki 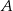 i
i 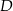 mają współrzędne
mają współrzędne 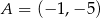 i
i 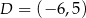 . Oblicz współrzędne wierzchołków
. Oblicz współrzędne wierzchołków 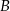 i
i 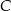 oraz pole rombu
oraz pole rombu 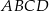 .
.
Punkty o współrzędnych 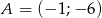 ,
, 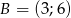 ,
, 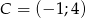 są wierzchołkami trapezu. Ramię trapezu
są wierzchołkami trapezu. Ramię trapezu 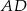 jest prostopadłe do podstaw
jest prostopadłe do podstaw 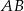 i
i 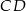 . Oblicz współrzędne punktu
. Oblicz współrzędne punktu 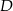 oraz pole powierzchni tego trapezu.
oraz pole powierzchni tego trapezu.
W kartezjańskim układzie współrzędnych 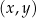 dany jest równoległobok
dany jest równoległobok 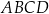 , w którym
, w którym 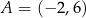 oraz
oraz 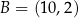 . Przekątne
. Przekątne 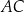 oraz
oraz 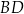 tego równoległoboku przecinają się w punkcie
tego równoległoboku przecinają się w punkcie 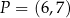 . Oblicz długość boku
. Oblicz długość boku 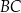 tego równoległoboku.
tego równoległoboku.
W kartezjańskim układzie współrzędnych 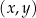 trapez
trapez 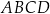 jest wpisany w okrąg o środku w punkcie
jest wpisany w okrąg o środku w punkcie 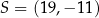 i promieniu
i promieniu 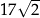 . Wierzchołek
. Wierzchołek 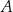 trapezu ma obie współrzędne ujemne, a odcinek
trapezu ma obie współrzędne ujemne, a odcinek 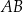 jest dłuższą z podstaw tego trapezu. Przekątna
jest dłuższą z podstaw tego trapezu. Przekątna 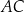 trapezu
trapezu 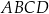 jest zawarta w prostej o równaniu
jest zawarta w prostej o równaniu 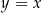 . Oblicz sinus kąta
. Oblicz sinus kąta 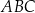 .
.
Kwadrat 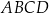 jest wpisany w okrąg o równaniu
jest wpisany w okrąg o równaniu 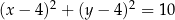 oraz
oraz 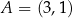 . Wyznacz równanie prostej zawierającej przekątną
. Wyznacz równanie prostej zawierającej przekątną 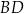 tego kwadratu.
tego kwadratu.
Punkt 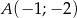 jest wierzchołkiem rombu, którego jeden z boków zawiera się w prostej
jest wierzchołkiem rombu, którego jeden z boków zawiera się w prostej 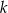 o równaniu
o równaniu 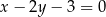 . Środkiem symetrii tego rombu jest punkt
. Środkiem symetrii tego rombu jest punkt 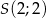 . Oblicz współrzędne pozostałych wierzchołków rombu i oblicz jego pole.
. Oblicz współrzędne pozostałych wierzchołków rombu i oblicz jego pole.
Punkt 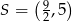 jest środkiem symetrii prostokąta
jest środkiem symetrii prostokąta 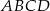 , którego pole jest równe 30, a bok
, którego pole jest równe 30, a bok 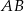 jest zawarty w prostej o równaniu
jest zawarty w prostej o równaniu 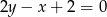 . Oblicz współrzędne wierzchołków prostokąta
. Oblicz współrzędne wierzchołków prostokąta 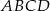 .
.
Dany jest okrąg 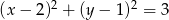 . Oblicz pole rombu opisanego na tym okręgu, jeśli kąt ostry rombu ma miarę
. Oblicz pole rombu opisanego na tym okręgu, jeśli kąt ostry rombu ma miarę 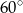 .
.
Dany jest okrąg 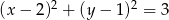 . Oblicz długości przekątnych rombu opisanego na tym okręgu, jeśli kąt ostry rombu ma miarę
. Oblicz długości przekątnych rombu opisanego na tym okręgu, jeśli kąt ostry rombu ma miarę 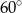 .
.
Przekątne 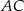 i
i 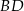 rombu
rombu 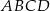 przecinają się w punkcie
przecinają się w punkcie 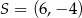 . Wyznacz równanie prostej zawierającej przekątną
. Wyznacz równanie prostej zawierającej przekątną 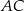 wiedząc, że prosta zawierająca przekątną
wiedząc, że prosta zawierająca przekątną 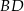 ma równanie
ma równanie 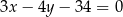 .
.
Przekątne rombu 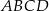 przecinają się w punkcie
przecinają się w punkcie 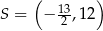 . Punkty
. Punkty 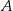 i
i 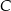 leżą na prostej o równaniu
leżą na prostej o równaniu 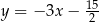 . Wyznacz równanie prostej
. Wyznacz równanie prostej 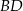 .
.
Przekątne rombu 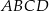 przecinają się w punkcie
przecinają się w punkcie 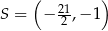 . Punkty
. Punkty 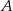 i
i 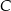 leżą na prostej o równaniu
leżą na prostej o równaniu 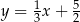 . Wyznacz równanie prostej
. Wyznacz równanie prostej 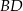 .
.
Na przedziale ![[− 1,7]](https://img.zadania.info/zad/2293968/HzadT0x.gif) określono dwie funkcje:
określono dwie funkcje: 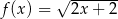 i
i 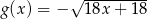 . Rozpatrujemy wszystkie trapezy
. Rozpatrujemy wszystkie trapezy 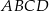 , których wierzchołki
, których wierzchołki 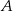 i
i 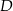 leżą na wykresie funkcji
leżą na wykresie funkcji 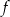 , a wierzchołki
, a wierzchołki 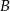 i
i 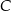 leżą na wykresie funkcji
leżą na wykresie funkcji 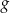 . Podstawy rozpatrywanych trapezów są równoległe do osi
. Podstawy rozpatrywanych trapezów są równoległe do osi 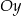 (zobacz rysunek).
(zobacz rysunek).
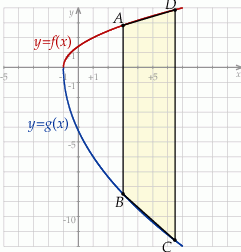
Wykaż, że jeżeli pierwsza współrzędna punktów 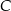 i
i 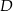 jest równa 7, a druga współrzędna punktu
jest równa 7, a druga współrzędna punktu 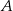 jest równa
jest równa 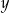 , to pole trapezu
, to pole trapezu 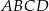 jest równe
jest równe
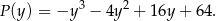
Punkt 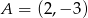 jest wierzchołkiem rombu
jest wierzchołkiem rombu 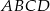 o polu równym 300. Punkt
o polu równym 300. Punkt 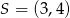 jest środkiem symetrii tego rombu. Wyznacz współrzędne pozostałych wierzchołków tego rombu.
jest środkiem symetrii tego rombu. Wyznacz współrzędne pozostałych wierzchołków tego rombu.
Czworokąt 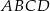 jest trapezem równoramiennym, który nie jest równoległobokiem. Wiedząc, że podstawami trapezu są odcinki
jest trapezem równoramiennym, który nie jest równoległobokiem. Wiedząc, że podstawami trapezu są odcinki 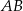 i
i 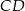 , przy czym
, przy czym 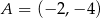 ,
, 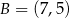 i
i 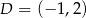 , oblicz pole oraz obwód trapezu.
, oblicz pole oraz obwód trapezu.

