Punkty przecięcia paraboli 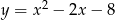 z prostą
z prostą 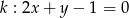 są końcami przekątnej rombu, którego pole jest równe 30. Oblicz współrzędne wierzchołków tego rombu.
są końcami przekątnej rombu, którego pole jest równe 30. Oblicz współrzędne wierzchołków tego rombu.
/Szkoła średnia/Geometria/Geometria analityczna/Czworokąt
Punkty 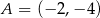 i
i 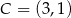 są wierzchołkami rombu
są wierzchołkami rombu 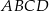 , którego wierzchołek
, którego wierzchołek 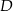 leży na prostej
leży na prostej 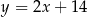 . Wyznacz współrzędne punktów
. Wyznacz współrzędne punktów 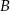 i
i 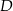 .
.
Dane są punkty 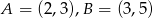 i
i 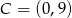 . Wyznacz współrzędne punktu
. Wyznacz współrzędne punktu 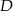 , dla którego czworokąt
, dla którego czworokąt 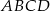 jest trapezem prostokątnym, którego kąt przy wierzchołku
jest trapezem prostokątnym, którego kąt przy wierzchołku 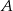 jest prosty.
jest prosty.
Punkty 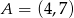 ,
, 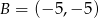 i
i 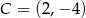 są wierzchołkami trapezu prostokątnego
są wierzchołkami trapezu prostokątnego 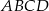 o podstawach
o podstawach 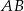 i
i 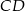 . Wyznacz współrzędne wierzchołka
. Wyznacz współrzędne wierzchołka 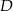 .
.
Dane są dwa przeciwległe wierzchołki 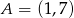 i
i 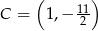 prostokąta
prostokąta 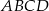 . Prosta o równaniu
. Prosta o równaniu 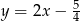 jest osią symetrii tego prostokąta. Oblicz współrzędne wierzchołków
jest osią symetrii tego prostokąta. Oblicz współrzędne wierzchołków 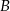 i
i 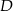 tego prostokąta.
tego prostokąta.
Wierzchołki trapezu 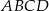 mają współrzędne:
mają współrzędne: 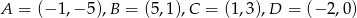 . Napisz równanie okręgu, który jest styczny do podstawy
. Napisz równanie okręgu, który jest styczny do podstawy 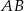 tego trapezu, a jego środek jest punktem przecięcia się prostych zawierających ramiona
tego trapezu, a jego środek jest punktem przecięcia się prostych zawierających ramiona 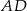 oraz
oraz 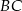 trapezu
trapezu 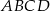 .
.
Wierzchołki trapezu 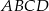 mają współrzędne:
mają współrzędne: 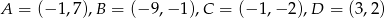 . Napisz równanie okręgu, który jest styczny do podstawy
. Napisz równanie okręgu, który jest styczny do podstawy 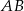 tego trapezu, a jego środek jest punktem przecięcia się przekątnych trapezu
tego trapezu, a jego środek jest punktem przecięcia się przekątnych trapezu  .
.
Dany jest równoległobok 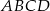 o wierzchołkach
o wierzchołkach 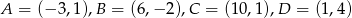 . Napisz równania prostych, w których zawarte są przekątne równoległoboku.
. Napisz równania prostych, w których zawarte są przekątne równoległoboku.
Punkty 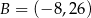 ,
, 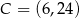 i
i 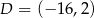 są wierzchołkami trapezu równoramiennego
są wierzchołkami trapezu równoramiennego 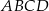 o podstawach
o podstawach 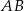 i
i 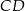 . Wyznacz współrzędne wierzchołka
. Wyznacz współrzędne wierzchołka 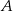 tego trapezu jeżeli wiadomo, że
tego trapezu jeżeli wiadomo, że 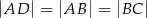 .
.
Dany jest równoległobok, którego boki zawierają się w prostych o równaniach: 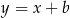 ,
, 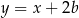 ,
, 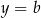 ,
, 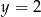 , gdzie liczba rzeczywista
, gdzie liczba rzeczywista 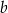 spełnia warunki:
spełnia warunki: 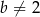 i
i 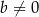 . Wyznacz wszystkie wartości parametru
. Wyznacz wszystkie wartości parametru 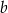 , dla których pole tego równoległoboku jest równe 1.
, dla których pole tego równoległoboku jest równe 1.
Dany jest równoległobok, którego boki zawierają się w prostych o równaniach: 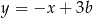 ,
, 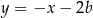 ,
, 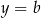 ,
, 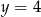 , gdzie liczba rzeczywista
, gdzie liczba rzeczywista 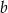 spełnia warunki:
spełnia warunki: 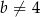 i
i 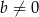 . Wyznacz wszystkie wartości parametru
. Wyznacz wszystkie wartości parametru 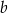 , dla których pole tego równoległoboku jest równe 20.
, dla których pole tego równoległoboku jest równe 20.
W okrąg o środku 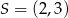 wpisano trapez w taki sposób, że jedna podstawa jest średnicą okręgu, a druga jest zawarta w prostej o równaniu
wpisano trapez w taki sposób, że jedna podstawa jest średnicą okręgu, a druga jest zawarta w prostej o równaniu 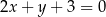 . Pole tego trapezu jest równe
. Pole tego trapezu jest równe 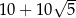 . Oblicz współrzędne tych wierzchołków trapezu, które są końcami jego krótszej podstawy.
. Oblicz współrzędne tych wierzchołków trapezu, które są końcami jego krótszej podstawy.
W trapezie równoramiennym 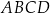 podstawa
podstawa 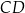 ma długość 5. Punkt
ma długość 5. Punkt 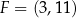 jest środkiem odcinka
jest środkiem odcinka 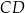 . Prosta o równaniu
. Prosta o równaniu 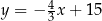 jest osią symetrii tego trapezu oraz
jest osią symetrii tego trapezu oraz 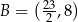 . Oblicz współrzędne wierzchołka
. Oblicz współrzędne wierzchołka 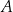 oraz pole tego trapezu.
oraz pole tego trapezu.
Dane są dwa wierzchołki 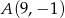 i
i 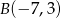 prostokąta
prostokąta 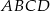 oraz punkt
oraz punkt 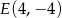 należący do boku CD.
należący do boku CD.
- Wyznacz równanie prostej zawierającej bok
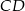 ;
; - Oblicz współrzędne wierzchołka C;
- Oblicz współrzędne punktu
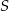 przecięcia się przekątnych tego prostokąta.
przecięcia się przekątnych tego prostokąta.
Jeden z boków kwadratu 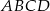 jest zawarty w prostej o równaniu
jest zawarty w prostej o równaniu 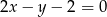 . Wierzchołek
. Wierzchołek 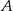 ma współrzędne
ma współrzędne 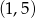 .
.
- Znajdź współrzędne pozostałych wierzchołków.
- Oblicz pole kwadratu
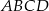 .
.
Jeden bok kwadratu opisanego okręgu o równaniu 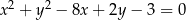 jest zawarty w prostej o równaniu
jest zawarty w prostej o równaniu 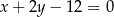 . Oblicz współrzędne wierzchołków tego kwadratu.
. Oblicz współrzędne wierzchołków tego kwadratu.
W układzie współrzędnych na płaszczyźnie punkty 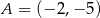 i
i 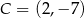 są przeciwległymi wierzchołkami deltoidu
są przeciwległymi wierzchołkami deltoidu 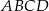 , w którym
, w którym 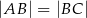 . Wyznacz równanie prostej
. Wyznacz równanie prostej 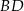 .
.
W układzie współrzędnych na płaszczyźnie punkty 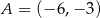 i
i 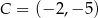 są przeciwległymi wierzchołkami deltoidu
są przeciwległymi wierzchołkami deltoidu 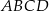 , w którym
, w którym 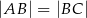 . Wyznacz równanie prostej
. Wyznacz równanie prostej 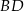 .
.
Dane są punkty 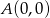 i
i 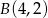 .
.
- Znajdź takie punkty
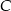 i
i 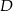 aby trójkąty
aby trójkąty 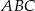 i
i 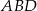 były równoboczne.
były równoboczne. - Znajdź równanie okręgu wpisanego w romb
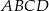 .
. - Oblicz pole figury, którą otrzymamy po usunięciu z rombu
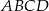 wnętrza wpisanego w niego koła.
wnętrza wpisanego w niego koła.
Punkty 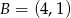 i
i 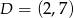 są przeciwległymi wierzchołkami rombu
są przeciwległymi wierzchołkami rombu 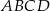 . Wyznacz równanie przekątnej
. Wyznacz równanie przekątnej 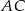 tego rombu.
tego rombu.
Punkty 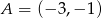 i
i 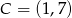 są przeciwległymi wierzchołkami rombu
są przeciwległymi wierzchołkami rombu 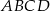 . Wyznacz równanie przekątnej
. Wyznacz równanie przekątnej 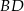 tego rombu.
tego rombu.
Dwa boki kwadratu zawierają się w prostych o równaniach 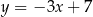 i
i 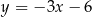 . Oblicz pole tego kwadratu.
. Oblicz pole tego kwadratu.
W kartezjańskim układzie współrzędnych 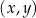 przekątne równoległoboku
przekątne równoległoboku 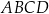 przecinają się w punkcie
przecinają się w punkcie 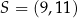 . Bok
. Bok 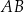 tego równoległoboku zawiera się w prostej o równaniu
tego równoległoboku zawiera się w prostej o równaniu 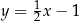 , a bok
, a bok 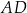 zawiera się w prostej o równaniu
zawiera się w prostej o równaniu 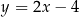 . Oblicz współrzędne wierzchołka
. Oblicz współrzędne wierzchołka 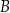 oraz długość odcinka
oraz długość odcinka 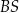 .
.
Prosta o równaniu 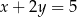 zawiera przekątną
zawiera przekątną 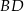 rombu
rombu 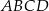 , którego bok ma długość 5. Wyznacz współrzędne wierzchołków rombu jeżeli
, którego bok ma długość 5. Wyznacz współrzędne wierzchołków rombu jeżeli 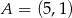 .
.
Odcinek o końcach 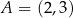 i
i 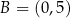 jest podstawą trapezu
jest podstawą trapezu 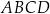 . Druga podstawa o środku w punkcie
. Druga podstawa o środku w punkcie 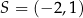 jest dwa razy dłuższa od podstawy
jest dwa razy dłuższa od podstawy 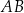 . Wyznacz współrzędne wierzchołków
. Wyznacz współrzędne wierzchołków 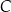 i
i 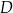 . Oblicz pole tego trapezu.
. Oblicz pole tego trapezu.

