Wierzchołki 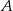 i
i 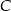 kwadratu
kwadratu 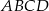 o polu 8 leżą na prostej o równaniu
o polu 8 leżą na prostej o równaniu 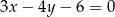 . Środek symetrii tego kwadratu ma współrzędne
. Środek symetrii tego kwadratu ma współrzędne 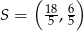 . Oblicz współrzędne punktów
. Oblicz współrzędne punktów 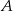 i
i 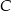 .
.
/Szkoła średnia/Geometria/Geometria analityczna/Czworokąt
Punkt 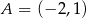 jest wierzchołkiem rombu o polu równym 20. Punkt
jest wierzchołkiem rombu o polu równym 20. Punkt 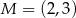 jest środkiem symetrii tego rombu. Wyznacz równanie okręgu wpisanego w ten romb.
jest środkiem symetrii tego rombu. Wyznacz równanie okręgu wpisanego w ten romb.
Wyznacz współrzędne punktu przecięcia się przekątnych czworokąta 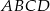 jeżeli
jeżeli 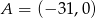 ,
, 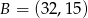 ,
, 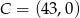 i
i 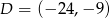 .
.
Punkty 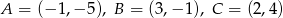 są kolejnymi wierzchołkami równoległoboku
są kolejnymi wierzchołkami równoległoboku 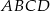 . Oblicz pole tego równoległoboku.
. Oblicz pole tego równoległoboku.
Oblicz pole równoległoboku 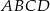 o wierzchołkach
o wierzchołkach 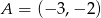 ,
, 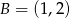 ,
, 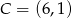 ,
, 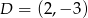 .
.
W równoległoboku 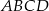 dane są wierzchołki
dane są wierzchołki 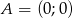 ,
, 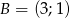 ,
, 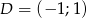 . Wyznacz wierzchołek
. Wyznacz wierzchołek 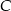 oraz środek symetrii tego równoległoboku.
oraz środek symetrii tego równoległoboku.
Wyznacz współrzędne wierzchołka 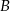 równoległoboku
równoległoboku 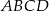 jeżeli
jeżeli 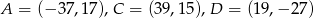 .
.
Przekątne deltoidu 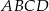 przecinają się w punkcie
przecinają się w punkcie 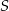 , który znajduje się w III ćwiartce układu współrzędnych. Wyznacz równanie okręgu opisanego na trójkącie
, który znajduje się w III ćwiartce układu współrzędnych. Wyznacz równanie okręgu opisanego na trójkącie 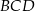 jeżeli okręgi opisane na trójkątach
jeżeli okręgi opisane na trójkątach 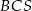 i
i 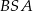 mają odpowiednio równania
mają odpowiednio równania 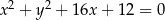 i
i 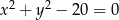 .
.
W trapezie 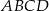 , w którym
, w którym 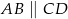 , dane są wierzchołki
, dane są wierzchołki 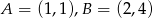 oraz punkt przecięcia przekątnych
oraz punkt przecięcia przekątnych 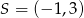 . Pole trapezu jest równe 36.
. Pole trapezu jest równe 36.
- Oblicz długość podstawy
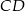 .
. - Wyznacz współrzędne wierzchołków
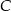 i
i 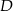 .
.
Dany jest prostokąt o wierzchołkach 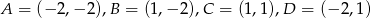 . Wyznacz wszystkie wartości współczynnika
. Wyznacz wszystkie wartości współczynnika 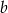 , dla których prosta o równaniu
, dla których prosta o równaniu 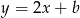 ma co najmniej jeden punkt wspólny z prostokątem
ma co najmniej jeden punkt wspólny z prostokątem 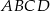 .
.
W kartezjańskim układzie współrzędnych dany jest romb 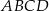 , którego bok
, którego bok 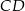 i przekątna
i przekątna 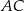 są zawarte w prostych o równaniach
są zawarte w prostych o równaniach 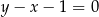 i
i 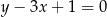 odpowiednio. Promień okręgu wpisanego w romb
odpowiednio. Promień okręgu wpisanego w romb 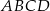 jest równy
jest równy 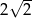 , a środek tego okręgu leży poniżej osi
, a środek tego okręgu leży poniżej osi 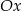 . Oblicz współrzędne punktu styczności okręgu wpisanego w romb
. Oblicz współrzędne punktu styczności okręgu wpisanego w romb 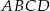 z jego bokiem
z jego bokiem 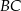 .
.
Wyznacz współrzędne środka okręgu opisanego na kwadracie, którego jeden z boków jest zawarty w prostej o równaniu 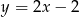 , a punkt
, a punkt 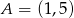 jest jego wierzchołkiem. Rozważ wszystkie przypadki.
jest jego wierzchołkiem. Rozważ wszystkie przypadki.
W układzie współrzędnych na płaszczyźnie punkty 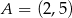 i
i 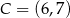 są przeciwległymi wierzchołkami kwadratu
są przeciwległymi wierzchołkami kwadratu 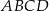 . Wyznacz równanie prostej
. Wyznacz równanie prostej 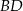 .
.
W kwadracie 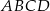 punkty
punkty 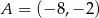 oraz
oraz 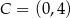 są końcami przekątnej. Wyznacz równanie prostej zawierającej przekątną
są końcami przekątnej. Wyznacz równanie prostej zawierającej przekątną 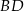 tego kwadratu.
tego kwadratu.
W układzie współrzędnych na płaszczyźnie punkty 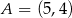 i
i 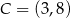 są przeciwległymi wierzchołkami kwadratu
są przeciwległymi wierzchołkami kwadratu 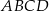 . Wyznacz równanie prostej
. Wyznacz równanie prostej 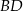 .
.
Pole równoległoboku 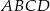 o danych wierzchołkach
o danych wierzchołkach 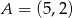 i
i 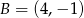 jest równe 26. Wyznacz współrzędne pozostałych wierzchołków równoległoboku, jeżeli jego przekątne przecinają się w punkcie leżącym na prostej
jest równe 26. Wyznacz współrzędne pozostałych wierzchołków równoległoboku, jeżeli jego przekątne przecinają się w punkcie leżącym na prostej 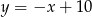 , który ma obie współrzędne będące liczbami całkowitymi.
, który ma obie współrzędne będące liczbami całkowitymi.

