Punkty 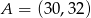 i
i 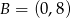 są sąsiednimi wierzchołkami czworokąta
są sąsiednimi wierzchołkami czworokąta 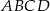 wpisanego w okrąg. Prosta o równaniu
wpisanego w okrąg. Prosta o równaniu 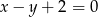 jest jedyną osią symetrii tego czworokąta i zawiera przekątną
jest jedyną osią symetrii tego czworokąta i zawiera przekątną 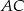 . Oblicz współrzędne wierzchołków
. Oblicz współrzędne wierzchołków 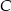 i
i 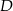 tego czworokąta.
tego czworokąta.
/Szkoła średnia/Geometria/Geometria analityczna/Czworokąt
Punkty 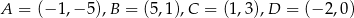 są kolejnymi wierzchołkami trapezu
są kolejnymi wierzchołkami trapezu 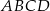 . Oblicz pole tego trapezu.
. Oblicz pole tego trapezu.
Wyznacz równanie okręgu wpisanego w kwadrat 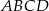 , gdzie
, gdzie 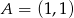 i
i 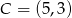 .
.
Wyznacz równanie okręgu opisanego na prostokącie  , w którym
, w którym 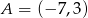 i
i 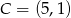 .
.
W okrąg o równaniu 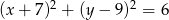 wpisano kwadrat. Oblicz pole tego kwadratu.
wpisano kwadrat. Oblicz pole tego kwadratu.
Przekątne prostokąta 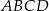 o polu
o polu 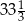 są zawarte w prostych o równaniach
są zawarte w prostych o równaniach 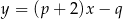 i
i 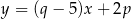 . Ponadto prosta
. Ponadto prosta 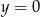 jest osią symetrii tego prostokąta. Oblicz obwód tego prostokąta.
jest osią symetrii tego prostokąta. Oblicz obwód tego prostokąta.
Przekątne prostokąta 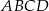 o obwodzie
o obwodzie 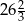 są zawarte w prostych o równaniach
są zawarte w prostych o równaniach 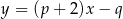 i
i 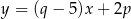 . Ponadto prosta
. Ponadto prosta 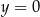 jest osią symetrii tego prostokąta. Oblicz pole tego prostokąta.
jest osią symetrii tego prostokąta. Oblicz pole tego prostokąta.
Punkt 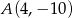 jest wierzchołkiem równoległoboku
jest wierzchołkiem równoległoboku 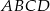 . Dwa boki równoległoboku zawierają się w prostych o równaniach
. Dwa boki równoległoboku zawierają się w prostych o równaniach 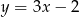 i
i 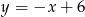 . Wyznacz pozostałe wierzchołki równoległoboku.
. Wyznacz pozostałe wierzchołki równoległoboku.
Przekątna 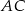 czworokąta
czworokąta 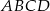 zawiera się w prostej o równaniu
zawiera się w prostej o równaniu 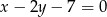 . Wierzchołki
. Wierzchołki 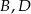 tego czworokąta mają współrzędne
tego czworokąta mają współrzędne 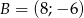 ,
, 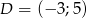 . Oblicz współrzędne punktu przecięcia się przekątnych czworokąta
. Oblicz współrzędne punktu przecięcia się przekątnych czworokąta 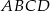 .
.
Wykaż, że punkt o współrzędnych 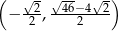 jest wierzchołkiem kwadratu opisanego na okręgu o równaniu
jest wierzchołkiem kwadratu opisanego na okręgu o równaniu
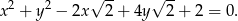
Punkty 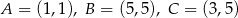 są wierzchołkami trapezu równoramiennego
są wierzchołkami trapezu równoramiennego 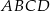 niebędącego równoległobokiem, w którym
niebędącego równoległobokiem, w którym 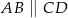 .
.
- Wyznacz równanie osi symetrii tego trapezu.
- Oblicz pole tego trapezu.
Przekątne kwadratu 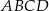 przecinają się w punkcie
przecinają się w punkcie 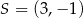 , a jeden z jego boków jest zawarty w prostej
, a jeden z jego boków jest zawarty w prostej 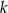 o równaniu
o równaniu 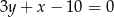 . Wyznacz współrzędne wierzchołków kwadratu
. Wyznacz współrzędne wierzchołków kwadratu 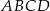 .
.
Dane są równania prostych 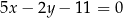 i
i 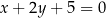 , w których zawierają się dwa boki równoległoboku. Punkt
, w których zawierają się dwa boki równoległoboku. Punkt 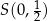 jest środkiem symetrii tego równoległoboku. Znajdź równania prostych, w których zawierają się pozostałe boki równoległoboku.
jest środkiem symetrii tego równoległoboku. Znajdź równania prostych, w których zawierają się pozostałe boki równoległoboku.
Wyznacz współrzędne punktu przecięcia przekątnych czworokąta 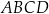 jeżeli
jeżeli 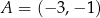 ,
, 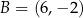 ,
, 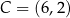 i
i 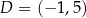 .
.
Wyznacz współrzędne punktu przecięcia przekątnych czworokąta 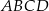 jeżeli
jeżeli 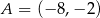 ,
, 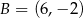 ,
, 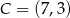 i
i 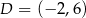 .
.
Na płaszczyźnie, w kartezjańskim układzie współrzędnych 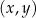 , punkty
, punkty 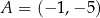 ,
, 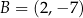 ,
, 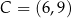 i
i 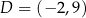 są wierzchołkami czworokąta
są wierzchołkami czworokąta 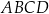 . Oblicz współrzędne punktu przecięcia przekątnych czworokąta
. Oblicz współrzędne punktu przecięcia przekątnych czworokąta 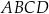 .
.
Napisz równanie okręgu opisanego na trapezie równoramiennym 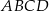 , jeżeli
, jeżeli 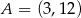 ,
, 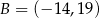 ,
, 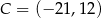 i
i 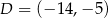 .
.
Punkty 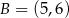 i
i 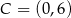 są wierzchołkami trapezu równoramiennego
są wierzchołkami trapezu równoramiennego 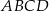 , którego podstawy
, którego podstawy 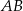 i
i 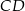 są prostopadłe do prostej
są prostopadłe do prostej 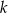 o równaniu
o równaniu 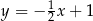 . Oblicz współrzędne pozostałych wierzchołków trapezu, wiedząc, że punkt
. Oblicz współrzędne pozostałych wierzchołków trapezu, wiedząc, że punkt 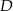 należy do prostej
należy do prostej 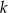 .
.
Dany jest równoległobok, którego boki zawierają się w prostych o równaniach: 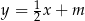 ,
, 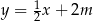 ,
, 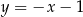 ,
, 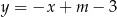 , gdzie
, gdzie 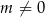 i
i 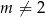 . Wyznacz wszystkie wartości parametru
. Wyznacz wszystkie wartości parametru 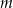 , dla których iloczyn długości dwóch wysokości tego równoległoboku, które nie są równoległe, jest równy
, dla których iloczyn długości dwóch wysokości tego równoległoboku, które nie są równoległe, jest równy 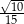 .
.
Punkty 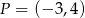 ,
, 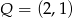 i
i 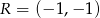 są środkami boków równoległoboku. Wyznacz współrzędne wierzchołków tego równoległoboku.
są środkami boków równoległoboku. Wyznacz współrzędne wierzchołków tego równoległoboku.
Przekątna 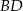 deltoidu zawiera się w prostej o równaniu
deltoidu zawiera się w prostej o równaniu 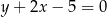 i ma taką samą długość jak przekątna
i ma taką samą długość jak przekątna 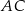 . Przekątne te przecinają się w punkcie
. Przekątne te przecinają się w punkcie 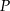 , takim że
, takim że 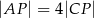 . Wierzchołek
. Wierzchołek 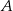 ma współrzędne
ma współrzędne 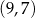 . Oblicz współrzędne wierzchołków
. Oblicz współrzędne wierzchołków 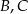 i
i 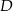 tego deltoidu.
tego deltoidu.
W kwadracie 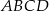 dane są wierzchołek
dane są wierzchołek 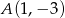 i równanie prostej
i równanie prostej 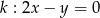 w której zawiera się jedna z przekątnych kwadratu. Znajdź współrzędne wierzchołka
w której zawiera się jedna z przekątnych kwadratu. Znajdź współrzędne wierzchołka 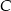 oraz oblicz pole tego kwadratu.
oraz oblicz pole tego kwadratu.
Dany jest romb o środku symetrii 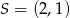 . Bok
. Bok 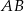 jest równoległy do prostej o równaniu
jest równoległy do prostej o równaniu 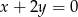 . Wektor
. Wektor 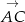 ma współrzędne
ma współrzędne ![[12 ,6 ]](https://img.zadania.info/zad/9275549/HzadT4x.gif) .
.
- Wyznacz współrzędne wszystkich wierzchołków rombu.
- Sprawdź czy miara kąta
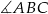 jest większa niż
jest większa niż 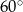 .
.

