Punkt 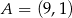 jest wierzchołkiem rombu
jest wierzchołkiem rombu 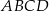 o polu 60. Przekątna
o polu 60. Przekątna 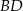 zawiera się w prostej
zawiera się w prostej 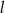 o równaniu
o równaniu 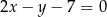 . Wyznacz równanie okręgu wpisanego w ten romb.
. Wyznacz równanie okręgu wpisanego w ten romb.
/Szkoła średnia/Geometria/Geometria analityczna/Czworokąt
Punkt 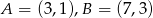 są kolejnymi wierzchołkami kwadratu
są kolejnymi wierzchołkami kwadratu 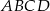 . Wyznacz współrzędne pozostałych wierzchołków tego kwadratu.
. Wyznacz współrzędne pozostałych wierzchołków tego kwadratu.
W kartezjańskim układzie współrzędnych 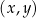 przekątne równoległoboku
przekątne równoległoboku 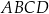 przecinają się w punkcie
przecinają się w punkcie 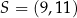 . Bok
. Bok 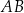 tego równoległoboku zawiera się w prostej o równaniu
tego równoległoboku zawiera się w prostej o równaniu 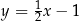 , a bok
, a bok 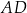 zawiera się w prostej o równaniu
zawiera się w prostej o równaniu 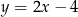 . Oblicz współrzędne wierzchołka
. Oblicz współrzędne wierzchołka 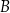 .
.
W kartezjańskim układzie współrzędnych  przekątne równoległoboku
przekątne równoległoboku 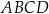 przecinają się w punkcie
przecinają się w punkcie 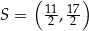 . Bok
. Bok 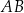 tego równoległoboku zawiera się w prostej o równaniu
tego równoległoboku zawiera się w prostej o równaniu 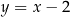 , a bok
, a bok 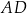 zawiera się w prostej o równaniu
zawiera się w prostej o równaniu 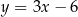 . Oblicz współrzędne wierzchołka
. Oblicz współrzędne wierzchołka 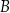 .
.
W rombie 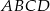 dane są
dane są 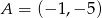 i punkt przecięcia przekątnych
i punkt przecięcia przekątnych 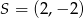 . Wierzchołek
. Wierzchołek 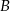 leży na prostej
leży na prostej 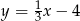 . Oblicz współrzędne pozostałych wierzchołków rombu.
. Oblicz współrzędne pozostałych wierzchołków rombu.
Punkty 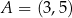 ,
, 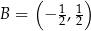 ,
, 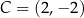 są kolejnymi wierzchołkami równoległoboku
są kolejnymi wierzchołkami równoległoboku 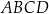 . Wyznacz równanie przekątnej
. Wyznacz równanie przekątnej 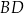 tego równoległoboku.
tego równoległoboku.
Punkty 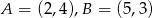 i
i 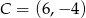 są sąsiednimi wierzchołkami czworokąta
są sąsiednimi wierzchołkami czworokąta 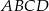 wpisanego w okrąg. Wierzchołek
wpisanego w okrąg. Wierzchołek 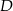 tego czworokąta leży na prostej o równaniu
tego czworokąta leży na prostej o równaniu 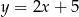 . Wyznacz współrzędne punktu
. Wyznacz współrzędne punktu 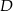 .
.
Oblicz pole czworokąta 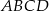 , którego wierzchołki mają współrzędne
, którego wierzchołki mają współrzędne 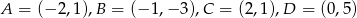 .
.
Oblicz pole czworokąta 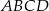 , którego wierzchołki mają współrzędne
, którego wierzchołki mają współrzędne 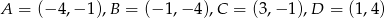 .
.
Punkty 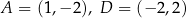 są kolejnymi wierzchołkami trapezu
są kolejnymi wierzchołkami trapezu 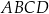 . Prosta
. Prosta 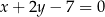 jest osią symetrii tego trapezu. Wyznacz współrzędne pozostałych wierzchołków tego trapezu.
jest osią symetrii tego trapezu. Wyznacz współrzędne pozostałych wierzchołków tego trapezu.
Dany jest kwadrat 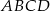 o polu 10 i wierzchołku
o polu 10 i wierzchołku 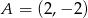 . Przekątna
. Przekątna 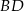 tego kwadratu ma równanie
tego kwadratu ma równanie 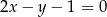 . Oblicz współrzędne pozostałych wierzchołków kwadratu.
. Oblicz współrzędne pozostałych wierzchołków kwadratu.
Punkt 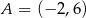 jest wierzchołkiem rombu
jest wierzchołkiem rombu 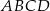 o polu 90. Przekątna
o polu 90. Przekątna 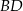 zawiera się w prostej
zawiera się w prostej 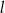 o równaniu
o równaniu 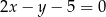 . Wyznacz długość boku tego rombu.
. Wyznacz długość boku tego rombu.
Punkty przecięcia paraboli 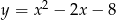 z prostą
z prostą 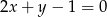 są końcami przekątnej rombu, którego pole wynosi 30. Oblicz współrzędne wierzchołków tego rombu oraz długość jego boku.
są końcami przekątnej rombu, którego pole wynosi 30. Oblicz współrzędne wierzchołków tego rombu oraz długość jego boku.
Wyznacz równanie okręgu wpisanego w deltoid, którego boki są zawarte w prostych o równaniach 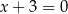 ,
, 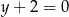 ,
, 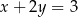 i
i 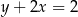 .
.
Sprawdź, czy czworokąt 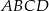 , gdzie
, gdzie 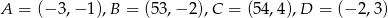 jest równoległobokiem. Odpowiedź uzasadnij.
jest równoległobokiem. Odpowiedź uzasadnij.
Punkty 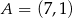 i
i 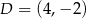 są kolejnymi wierzchołkami trapezu równoramiennego
są kolejnymi wierzchołkami trapezu równoramiennego 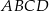 . Podstawa
. Podstawa 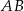 zawiera się w prostej o równaniu
zawiera się w prostej o równaniu 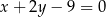 . Osią symetrii tego trapezu jest prosta o równaniu
. Osią symetrii tego trapezu jest prosta o równaniu 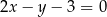 . Oblicz współrzędne wierzchołków
. Oblicz współrzędne wierzchołków 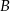 i
i 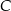 trapezu.
trapezu.
Wykaż, że czworokąt o wierzchołkach 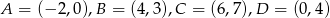 jest trapezem.
jest trapezem.
Prosta 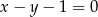 jest osią symetrii pewnego czworokąta wpisanego w okrąg. Punkty
jest osią symetrii pewnego czworokąta wpisanego w okrąg. Punkty 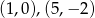 są jego wierzchołkami. Znajdź pozostałe wierzchołki.
są jego wierzchołkami. Znajdź pozostałe wierzchołki.
Dane są dwa wierzchołki 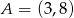 i
i 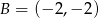 prostokąta
prostokąta 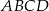 oraz punkt
oraz punkt 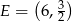 leżący na prostej
leżący na prostej 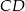 . Wyznacz współrzędne wierzchołków
. Wyznacz współrzędne wierzchołków 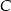 i
i  tego prostokąta.
tego prostokąta.
Oblicz obwód czworokąta o wierzchołkach: 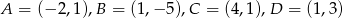 .
.
Dane są punkty 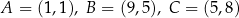 .
.
-
Wyznacz punkt
 tak, aby czworokąt
tak, aby czworokąt 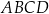 był trapezem prostokątnym, którego kąt przy wierzchołku
był trapezem prostokątnym, którego kąt przy wierzchołku 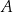 jest prosty.
jest prosty. -
Czy w ten trapez można wpisać okrąg?
Punkty 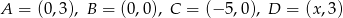 , gdzie
, gdzie 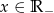 są kolejnymi wierzchołkami czworokąta
są kolejnymi wierzchołkami czworokąta 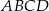 . Oblicz wartość
. Oblicz wartość  , dla której w czworokąt
, dla której w czworokąt 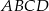 można wpisać okrąg.
można wpisać okrąg.

