Trójkąty równoboczne 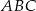 i
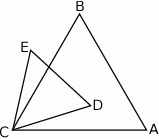
i 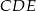 są położone tak, jak na poniższym rysunku. Wykaż, że
są położone tak, jak na poniższym rysunku. Wykaż, że 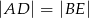 .
.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Trójkąty równoboczne 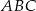 i
i 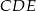 są położone tak, jak na poniższym rysunku. Wykaż, że
są położone tak, jak na poniższym rysunku. Wykaż, że 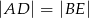 .
.

Z punktu 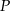 należącego do boku
należącego do boku 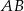 trójkąta równobocznego
trójkąta równobocznego 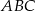 poprowadzono półprostą dzielącą trójkąt na dwie figury o równych polach. Oblicz tangens kąta jaki tworzy ta półprosta z odcinkiem
poprowadzono półprostą dzielącą trójkąt na dwie figury o równych polach. Oblicz tangens kąta jaki tworzy ta półprosta z odcinkiem 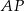 , jeśli
, jeśli 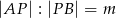 i
i 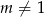 .
.
W trójkącie równobocznym 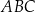 o wysokości
o wysokości 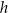 obrano punkt
obrano punkt 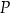 , z którego poprowadzono odcinki prostopadłe do boków tego trójkąta. Wykaż, że suma długości tych odcinków jest równa
, z którego poprowadzono odcinki prostopadłe do boków tego trójkąta. Wykaż, że suma długości tych odcinków jest równa 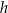 .
.
Wykaż, że trójkąt, którego długości boków są trzema kolejnymi wyrazami ciągu geometrycznego, miary kątów zaś trzema kolejnymi wyrazami ciągu arytmetycznego jest trójkątem równobocznym.
W trójkąt równoboczny wpisane są 3 koła o równych promieniach, przy czym każde koło jest styczne do dwóch boków trójkąta oraz do dwóch pozostałych kół. Oblicz stosunek sumy pól tych kół do pola trójkąta.
Na bokach trójkąta równobocznego 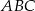 (na zewnątrz tego trójkąta) zbudowano kwadraty
(na zewnątrz tego trójkąta) zbudowano kwadraty 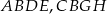 i
i 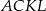 . Udowodnij, że trójkąt
. Udowodnij, że trójkąt 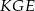 jest równoboczny.
jest równoboczny.
W trójkąt równoboczny o boku długości 6 cm wpisano kwadrat. Oblicz pole tego kwadratu.
Znaleźć pole kwadratu wpisanego w trójkąt równoboczny o boku 4 cm.
Na bokach trójkąta równobocznego zbudowano dwa kwadraty w sposób pokazany na rysunku.
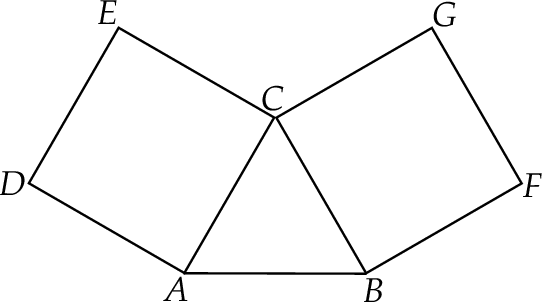
Wykaż, że punkty 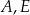 i
i 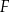 są wierzchołkami trójkąta prostokątnego.
są wierzchołkami trójkąta prostokątnego.
Znaleźć pole kwadratu wpisanego w trójkąt równoboczny o boku 4. Jakie pole ma koło opisane na tym kwadracie?
