Suma reszt jakie otrzymujemy dzieląc wielomian 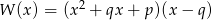 przez dwumiany
przez dwumiany 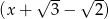 i
i 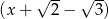 jest równa
jest równa 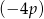 , gdzie
, gdzie 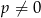 . Oblicz
. Oblicz 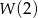 .
.
/Szkoła średnia/Funkcje/Wielomiany/Dzielenie z resztą
Wielomian 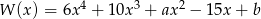 jest podzielny przez trójmian
jest podzielny przez trójmian 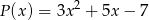 . Wyznacz liczby
. Wyznacz liczby  i
i 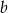 .
.
Dany jest wielomian 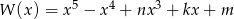 . Wyznacz wszystkie wartości parametrów
. Wyznacz wszystkie wartości parametrów 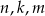 dla których reszta z dzielenia wielomianu
dla których reszta z dzielenia wielomianu 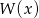 przez wielomian
przez wielomian 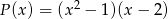 jest równa
jest równa 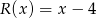 .
.
Dla jakich wartości 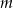 reszta z dzielenia wielomianu
reszta z dzielenia wielomianu 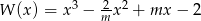 przez dwumian
przez dwumian 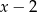 jest mniejsza lub równa 6?
jest mniejsza lub równa 6?
Dla jakich wartości 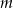 reszta z dzielenia wielomianu
reszta z dzielenia wielomianu 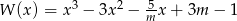 przez dwumian
przez dwumian 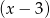 jest niewiększa od 3?
jest niewiększa od 3?
Dany jest wielomian 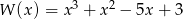 .
.
- Oblicz resztę z dzielenia tego wielomianu przez dwumian
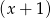 .
. - Oblicz miejsca zerowe tego wielomianu.
- Rozwiąż nierówność
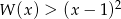 .
.
Nie wykonując dzielenia, wyznacz resztę z dzielenia wielomianu 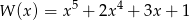 przez
przez 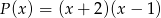 .
.
Dla jakiej wartości parametru 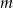 wielomian
wielomian 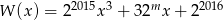 jest podzielny przez dwumian
jest podzielny przez dwumian 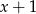 .
.
Wielomian 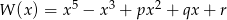 jest podzielny przez wielomian
jest podzielny przez wielomian 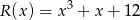 . Wyznacz liczby
. Wyznacz liczby 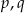 i
i  .
.
Wielomian 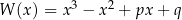 można dwukrotnie podzielić bez reszty przez dwumian
można dwukrotnie podzielić bez reszty przez dwumian 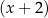 . Oblicz
. Oblicz 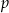 i
i 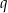 .
.
Reszta z dzielenia wielomianu 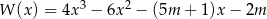 przez dwumian
przez dwumian 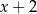 jest równa
jest równa 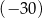 . Oblicz
. Oblicz 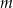 i dla wyznaczonej wartości
i dla wyznaczonej wartości 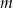 rozwiąż nierówność
rozwiąż nierówność 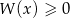 .
.
Reszta z dzielenia wielomianu 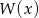 przez wielomian
przez wielomian 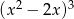 jest równa
jest równa 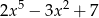 . Oblicz resztę z dzielenia wielomianu
. Oblicz resztę z dzielenia wielomianu 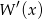 przez dwumian
przez dwumian 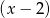 .
.
Reszta z dzielenia wielomianu 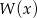 przez
przez 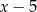 jest równa 4. Oblicz resztę z dzielenia wielomianu
jest równa 4. Oblicz resztę z dzielenia wielomianu 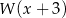 przez wielomian
przez wielomian 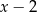 .
.
Reszta z dzielenia wielomianu 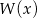 przez
przez 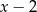 jest równa 7. Oblicz resztę z dzielenia wielomianu
jest równa 7. Oblicz resztę z dzielenia wielomianu 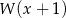 przez wielomian
przez wielomian 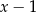 .
.
Reszta z dzielenia wielomianu 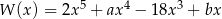 przez trójmian
przez trójmian 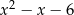 jest równa
jest równa 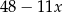 . Oblicz resztę z dzielenia wielomianu
. Oblicz resztę z dzielenia wielomianu 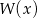 przez trójmian
przez trójmian 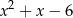 .
.
Wyznacz wszystkie wartości parametrów 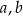 i
i  , dla których wielomian
, dla których wielomian
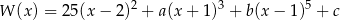
jest podzielny przez wielomian 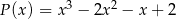 .
.
Reszta z dzielenia wielomianu 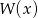 przez trójmian kwadratowy
przez trójmian kwadratowy 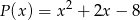 jest równa
jest równa 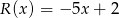 . Wyznacz resztę z dzielenia tego wielomianu przez dwumian
. Wyznacz resztę z dzielenia tego wielomianu przez dwumian 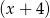 .
.
Dla jakich wartości parametru 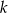 reszta z dzielenia wielomianu
reszta z dzielenia wielomianu 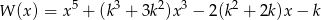 przez dwumian
przez dwumian 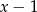 jest nie większa od (–2)?
jest nie większa od (–2)?
Dany jest wielomian 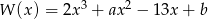 . Liczba 3 jest jednym z pierwiastków tego wielomianu. Reszta z dzielenia wielomianu
. Liczba 3 jest jednym z pierwiastków tego wielomianu. Reszta z dzielenia wielomianu 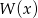 przez
przez 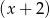 jest równa 20. Oblicz współczynniki
jest równa 20. Oblicz współczynniki  i
i 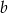 oraz pozostałe pierwiastki wielomianu
oraz pozostałe pierwiastki wielomianu 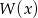 .
.
Reszta z dzielenia wielomianu 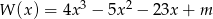 przez dwumian
przez dwumian 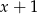 jest równa 20. Oblicz wartość współczynnika
jest równa 20. Oblicz wartość współczynnika 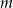 oraz pierwiastki tego wielomianu.
oraz pierwiastki tego wielomianu.
Reszta z dzielenia wielomianu 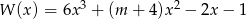 przez dwumian
przez dwumian 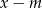 jest równa 8. Oblicz wartość
jest równa 8. Oblicz wartość 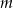 oraz pierwiastki tego wielomianu.
oraz pierwiastki tego wielomianu.
Reszty z dzielenia wielomianu 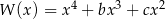 przez dwumiany
przez dwumiany 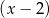 i
i 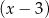 są odpowiednio równe
są odpowiednio równe 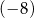 oraz
oraz 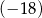 . Oblicz resztę z dzielenia wielomianu
. Oblicz resztę z dzielenia wielomianu 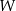 przez dwumian
przez dwumian 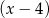 .
.
Dla jakich wartości parametru  , wielomian
, wielomian 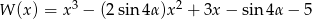 jest podzielny przez dwumian
jest podzielny przez dwumian 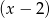 ?
?

