Wyznacz resztę z dzielenia wielomianu 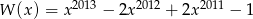 przez wielomian
przez wielomian 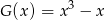 .
.
/Szkoła średnia/Funkcje/Wielomiany/Dzielenie z resztą
W wyniku dzielenia wielomianu 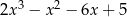 przez dwumian
przez dwumian 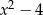 otrzymujemy resztę postaci
otrzymujemy resztę postaci 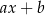 . Oblicz
. Oblicz  i
i 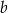 .
.
Dla jakich wartości parametru 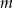 reszta z dzielenia wielomianu
reszta z dzielenia wielomianu
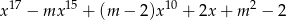
przez dwumian 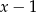 jest równa 3?
jest równa 3?
Dla jakich wartości parametru 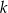 reszta z dzielenia wielomianu
reszta z dzielenia wielomianu
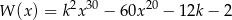
przez dwumian 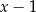 jest równa 2?
jest równa 2?
Reszta z dzielenia wielomianu 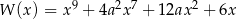 przez dwumian
przez dwumian 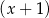 jest równa 2. Oblicz resztę z dzielenia wielomianu
jest równa 2. Oblicz resztę z dzielenia wielomianu 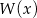 przez dwumian
przez dwumian 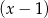 .
.
Wielomian 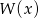 przy dzieleniu przez dwumiany
przy dzieleniu przez dwumiany 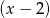 ,
, 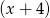 daje reszty odpowiednio równe -3 oraz -51. Wyznacz resztę z dzielenia wielomianu
daje reszty odpowiednio równe -3 oraz -51. Wyznacz resztę z dzielenia wielomianu 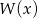 przez wielomian
przez wielomian 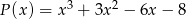 , wiedząc, że liczba -1 jest miejscem zerowym wielomianu
, wiedząc, że liczba -1 jest miejscem zerowym wielomianu 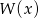 .
.
Wielomian 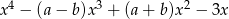 jest podzielny przez wielomian
jest podzielny przez wielomian 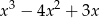 . Oblicz
. Oblicz  i
i 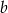 .
.
Przy dzieleniu wielomianu 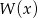 przez dwumian
przez dwumian 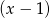 otrzymujemy iloraz
otrzymujemy iloraz 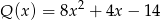 oraz resztę
oraz resztę 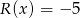 . Oblicz pierwiastki wielomianu
. Oblicz pierwiastki wielomianu 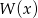 .
.
Reszta z dzielenia wielomianu 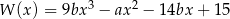 przez trójmian
przez trójmian 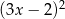 wynosi 3. Oblicz
wynosi 3. Oblicz  i
i 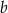 . Dla wyznaczonych wartości
. Dla wyznaczonych wartości  i
i 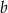 rozwiąż nierówność
rozwiąż nierówność 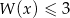 .
.
Niech ciąg 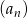 , dla
, dla 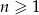 , będzie resztą z dzielenia wielomianu
, będzie resztą z dzielenia wielomianu 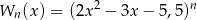 przez dwumian
przez dwumian 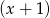 . Oblicz sumę dziesięciu początkowych wyrazów ciągu
. Oblicz sumę dziesięciu początkowych wyrazów ciągu 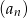 .
.
Reszta z dzielenia wielomianu 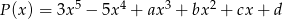 przez wielomian
przez wielomian 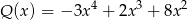 jest taka sama jak reszta z dzielenia wielomianu
jest taka sama jak reszta z dzielenia wielomianu 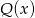 przez wielomian
przez wielomian 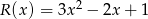 . Oblicz wartości współczynników
. Oblicz wartości współczynników 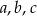 i
i 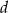 .
.
Reszta z dzielenia wielomianu 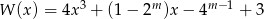 przez dwumian
przez dwumian 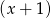 jest równa -2.
jest równa -2.
- Wyznacz wartość parametru
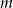 .
. - Dla wyznaczonej wartości parametru
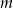 rozwiąż nierówność
rozwiąż nierówność 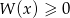 .
.
Wielomian 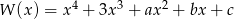 jest podzielny przez trójmian
jest podzielny przez trójmian 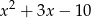 , a przy dzieleniu przez dwumian
, a przy dzieleniu przez dwumian 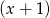 daje resztę -36. Wyznacz współczynniki
daje resztę -36. Wyznacz współczynniki 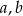 i
i  wielomianu.
wielomianu.
Reszta z dzielenia wielomianu 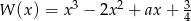 przez dwumian
przez dwumian 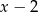 jest równa 1. Oblicz wartość współczynnika
jest równa 1. Oblicz wartość współczynnika  .
.
Reszta z dzielenia wielomianu 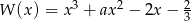 przez dwumian
przez dwumian 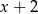 jest równa 1. Oblicz wartość współczynnika
jest równa 1. Oblicz wartość współczynnika  .
.
Wiedząc, że wielomian 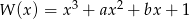 jest podzielny przez wielomian
jest podzielny przez wielomian 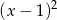 , oblicz
, oblicz  i
i 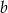 .
.
Dany jest wielomian 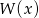 stopnia
stopnia 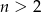 , którego suma wszystkich współczynników jest równa 4, a suma współczynników przy potęgach o wykładnikach nieparzystych jest równa sumie współczynników przy potęgach o wykładnikach parzystych. Wykaż, że reszta
, którego suma wszystkich współczynników jest równa 4, a suma współczynników przy potęgach o wykładnikach nieparzystych jest równa sumie współczynników przy potęgach o wykładnikach parzystych. Wykaż, że reszta 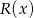 z dzielenia tego wielomianu przez wielomian
z dzielenia tego wielomianu przez wielomian 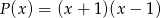 jest równa
jest równa 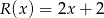 .
.
Reszta z dzielenia wielomianu 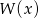 przez wielomian
przez wielomian 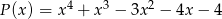 jest wielomianem
jest wielomianem 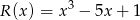 . Wyznacz resztę z dzielenia tego wielomianu przez wielomian
. Wyznacz resztę z dzielenia tego wielomianu przez wielomian 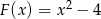 .
.
Reszta z dzielenia wielomianu 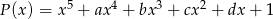 przez dwumian
przez dwumian 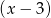 jest równa 1. Wykaż, że jeżeli liczby
jest równa 1. Wykaż, że jeżeli liczby 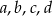 są liczbami całkowitymi to wielomian
są liczbami całkowitymi to wielomian 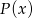 nie ma pierwiastków wymiernych.
nie ma pierwiastków wymiernych.
Reszty z dzielenia wielomianu 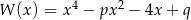 przez dwumiany
przez dwumiany 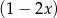 i
i 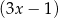 są odpowiednio równe
są odpowiednio równe 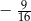 i
i 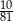 . Oblicz resztę z dzielenia wielomianu
. Oblicz resztę z dzielenia wielomianu 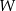 przez dwumian
przez dwumian 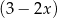 .
.
Dany jest wielomian 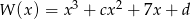 .
.
- Wyznacz wartości współczynników
 i
i 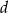 wielomianu
wielomianu 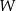 , wiedząc, że jest podzielny przez dwumian
, wiedząc, że jest podzielny przez dwumian 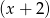 , zaś przy dzieleniu przez dwumian
, zaś przy dzieleniu przez dwumian 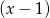 otrzymujemy resztę 3.
otrzymujemy resztę 3. - Dla
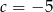 i
i 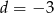 rozwiąż nierówność
rozwiąż nierówność 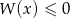 .
.
Wykaż, że jeżeli wielomian 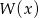 jest podzielny przez
jest podzielny przez 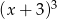 , to wielomian
, to wielomian 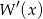 jest podzielny przez
jest podzielny przez 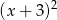 .
.

