Objętość ostrosłupa prawidłowego czworokątnego jest równa 384. Wysokość ściany bocznej tego ostrosłupa tworzy z płaszczyzną podstawy kąt o mierze  taki, że
taki, że 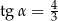 .
.
Oblicz wysokość ściany bocznej tego ostrosłupa.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Objętość ostrosłupa prawidłowego czworokątnego jest równa 384. Wysokość ściany bocznej tego ostrosłupa tworzy z płaszczyzną podstawy kąt o mierze  taki, że
taki, że 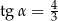 .
.

Oblicz wysokość ściany bocznej tego ostrosłupa.
Objętość ostrosłupa prawidłowego czworokątnego jest równa 400. Wysokość ściany bocznej tego ostrosłupa tworzy z płaszczyzną podstawy kąt o mierze  taki, że
taki, że 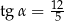 .
.
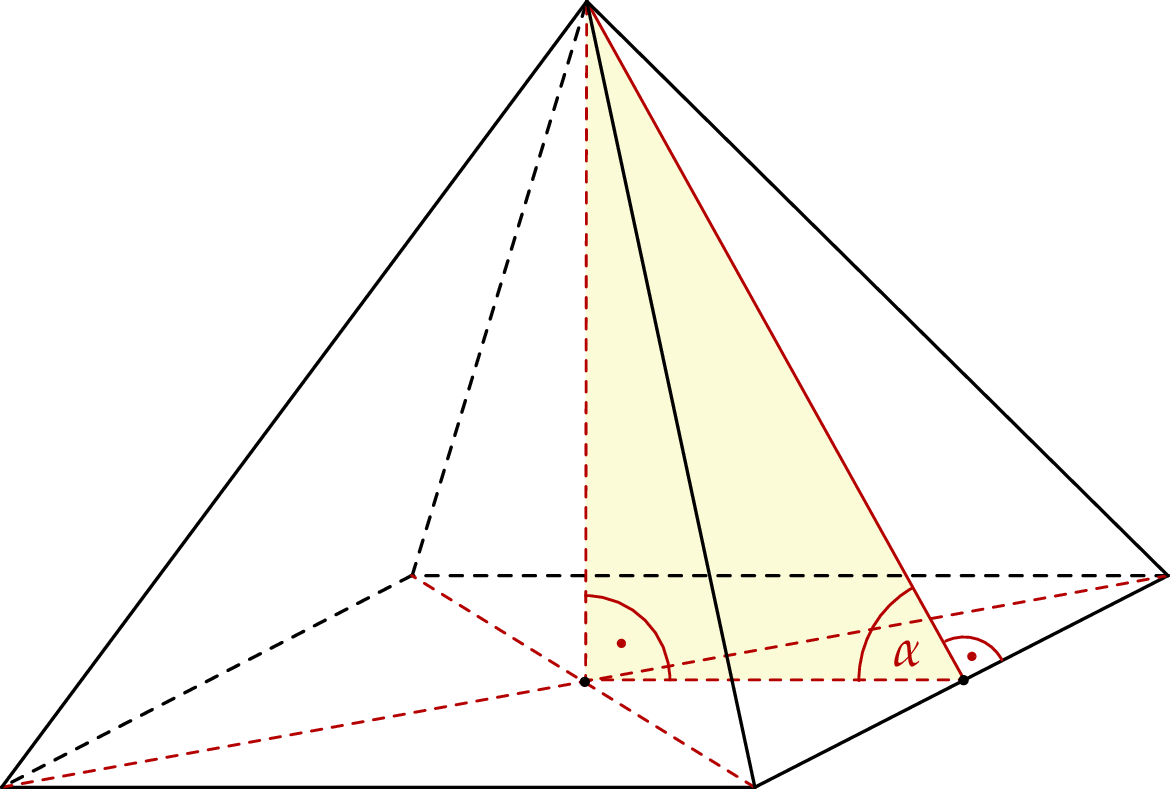
Oblicz wysokość ściany bocznej tego ostrosłupa.
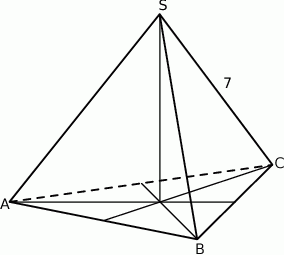
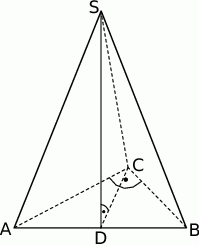
Podstawą ostrosłupa trójkątnego 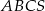 jest trójkąt prostokątny
jest trójkąt prostokątny 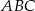 , w którym
, w którym 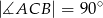 i
i 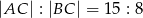 (zobacz rysunek). Punkt
(zobacz rysunek). Punkt 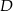 jest środkiem okręgu opisanego na trójkącie
jest środkiem okręgu opisanego na trójkącie 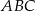 , a odcinek
, a odcinek 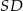 jest wysokością ostrosłupa. Objętość ostrosłupa jest równa 8, a pole ściany
jest wysokością ostrosłupa. Objętość ostrosłupa jest równa 8, a pole ściany 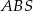 jest równe 17. Oblicz długość krawędzi
jest równe 17. Oblicz długość krawędzi 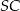 ostrosłupa
ostrosłupa
W ostrosłupie prawidłowym trójkątnym kąt płaski przy wierzchołku ostrosłupa ma miarę  , zaś odległość wierzchołka podstawy od krawędzi bocznej, do której nie należy, jest równa
, zaś odległość wierzchołka podstawy od krawędzi bocznej, do której nie należy, jest równa 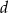 . Oblicz objętość i pole powierzchni całkowitej tego ostrosłupa.
. Oblicz objętość i pole powierzchni całkowitej tego ostrosłupa.
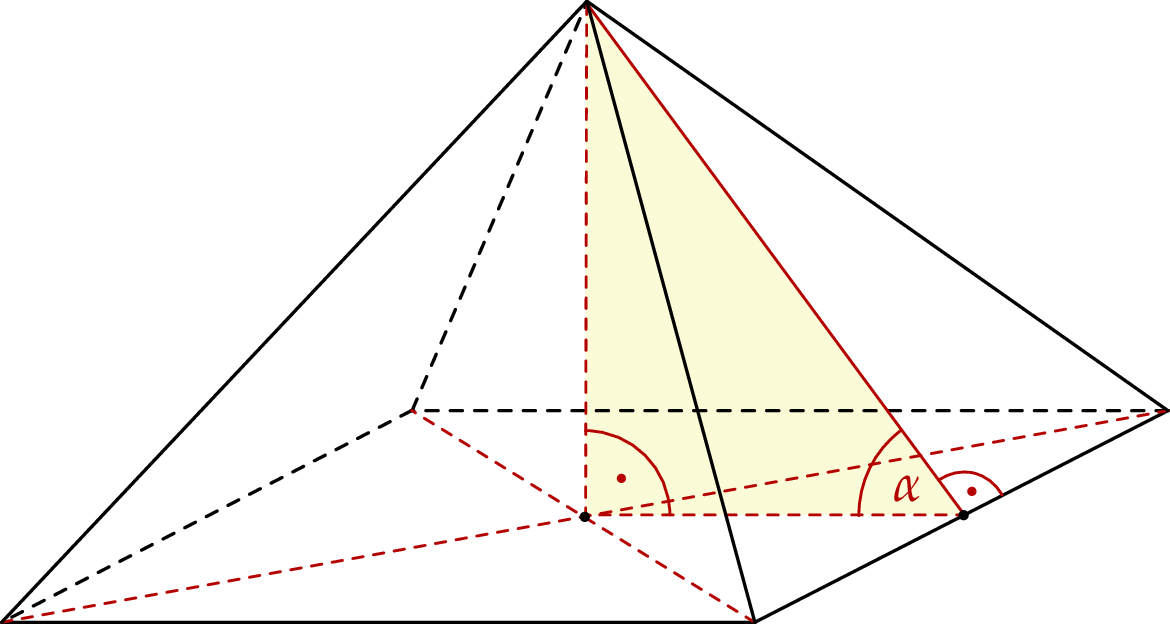
W ostrosłupie prawidłowym czworokątnym o krawędzi podstawy 18 cm, kąt między wysokościami przeciwległych ścian bocznych ma miarę 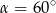 . Oblicz pole powierzchni bocznej tego ostrosłupa. Wykonaj odpowiedni rysunek i zaznacz kąt
. Oblicz pole powierzchni bocznej tego ostrosłupa. Wykonaj odpowiedni rysunek i zaznacz kąt  .
.
W ostrosłupie prawidłowym czworokątnym o krawędzi podstawy 12 cm, kąt między wysokościami przeciwległych ścian bocznych ma miarę 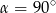 . Oblicz pole powierzchni bocznej tego ostrosłupa. Wykonaj odpowiedni rysunek i zaznacz kąt
. Oblicz pole powierzchni bocznej tego ostrosłupa. Wykonaj odpowiedni rysunek i zaznacz kąt  .
.
Ostrosłup prawidłowy trójkątny przecięto płaszczyzną przechodzącą przez krawędź podstawy długości  i środek wysokości ostrosłupa. Płaszczyzna ta jest nachylona do płaszczyzny podstawy pod kątem
i środek wysokości ostrosłupa. Płaszczyzna ta jest nachylona do płaszczyzny podstawy pod kątem  . Oblicz objętość i pole powierzchni bocznej ostrosłupa.
. Oblicz objętość i pole powierzchni bocznej ostrosłupa.
Podstawą ostrosłupa jest prostokąt o bokach 6 cm i 8 cm. Każda krawędź boczna jest nachylona do płaszczyzny podstawy pod katem 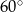 . Oblicz pole powierzchni ostrosłupa.
. Oblicz pole powierzchni ostrosłupa.
Krawędź boczna ostrosłupa prawidłowego trójkątnego jest nachylona do płaszczyzny podstawy pod kątem 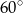 . Odległość spodka wysokości ostrosłupa od krawędzi bocznej jest równa 4. Oblicz objętość tego ostrosłupa.
. Odległość spodka wysokości ostrosłupa od krawędzi bocznej jest równa 4. Oblicz objętość tego ostrosłupa.
W ostrosłupie prawidłowym trójkątnym krawędź boczna ma długość 6, a pole ściany bocznej jest równe 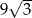 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
Odległość środka podstawy ostrosłupa prawidłowego czworokątnego od krawędzi bocznej równa się  , a kąt płaski ściany bocznej przy wierzchołku ostrosłupa równa się
, a kąt płaski ściany bocznej przy wierzchołku ostrosłupa równa się 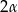 . Oblicz wysokość ostrosłupa.
. Oblicz wysokość ostrosłupa.
Podstawą ostrosłupa 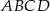 jest trójkąt równoramienny
jest trójkąt równoramienny 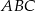 , w którym
, w którym 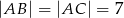 ,
, 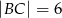 . Krawędzie boczne mają długości:
. Krawędzie boczne mają długości: 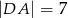 ,
, 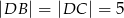 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
W ostrosłupie prawidłowym czworokątnym wysokości przeciwległych ścian bocznych, poprowadzone z wierzchołka ostrosłupa, są do siebie prostopadłe.
Podstawą ostrosłupa 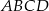 jest trójkąt równoramienny o podstawie
jest trójkąt równoramienny o podstawie 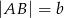 i kącie
i kącie  pomiędzy ramionami. Krawędź
pomiędzy ramionami. Krawędź 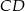 jest wysokością ostrosłupa, a kąt nachylenia ściany
jest wysokością ostrosłupa, a kąt nachylenia ściany 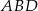 do podstawy ostrosłupa jest równy
do podstawy ostrosłupa jest równy 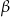 . Oblicz objętość i pole powierzchni całkowitej tego ostrosłupa.
. Oblicz objętość i pole powierzchni całkowitej tego ostrosłupa.
Dane są dwie bryły: stożek, w którym długość promienia podstawy jest równa 2 dm i wysokość ma długość 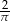 dm oraz ostrosłup prawidłowy trójkątny, w którym krawędź podstawy ma długość 4 dm. Wiedząc, że objętości tych brył są równe, wyznacz kąt nachylenia ściany bocznej ostrosłupa do jego podstawy.
dm oraz ostrosłup prawidłowy trójkątny, w którym krawędź podstawy ma długość 4 dm. Wiedząc, że objętości tych brył są równe, wyznacz kąt nachylenia ściany bocznej ostrosłupa do jego podstawy.
Podstawą ostrosłupa 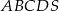 jest kwadrat
jest kwadrat 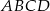 . Trójkąt równoramienny
. Trójkąt równoramienny 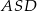 ma ramię długości 15 i jest prostopadły do podstawy ostrosłupa. Krawędź
ma ramię długości 15 i jest prostopadły do podstawy ostrosłupa. Krawędź 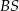 ma długość 17. Oblicz pole przekroju ostrosłupa płaszczyzną
ma długość 17. Oblicz pole przekroju ostrosłupa płaszczyzną 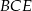 , gdzie
, gdzie 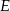 jest środkiem krawędzi
jest środkiem krawędzi 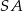 .
.
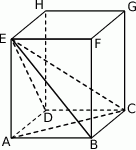
W graniastosłupie prawidłowym czworokątnym 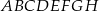 przekątna
przekątna 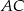 podstawy ma długość 4. Kąt
podstawy ma długość 4. Kąt 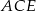 jest równy
jest równy 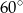 . Oblicz objętość ostrosłupa
. Oblicz objętość ostrosłupa 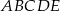 przedstawionego na poniższym rysunku.
przedstawionego na poniższym rysunku.
Dany jest ostrosłup prawidłowy sześciokątny. Wysokość ściany bocznej tego ostrosłupa jest nachylona do płaszczyzny podstawy pod kątem 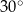 i ma długość równą 6 (zobacz rysunek).
i ma długość równą 6 (zobacz rysunek).
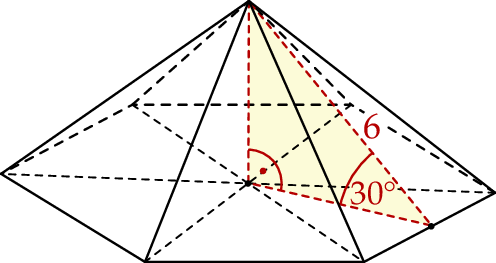
Oblicz objętość i pole powierzchni całkowitej tego ostrosłupa.
Krawędź boczna ostrosłupa prawidłowego czworokątnego jest nachylona do płaszczyzny podstawy pod kątem  takim, że
takim, że 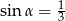 . Oblicz cosinus kąta nachylenia ściany bocznej do płaszczyzny podstawy.
. Oblicz cosinus kąta nachylenia ściany bocznej do płaszczyzny podstawy.
W ostrosłupie prawidłowym trójkątnym wysokość ściany bocznej ma długość 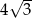 , a ściana boczna jest nachylona do płaszczyzny podstawy pod kątem
, a ściana boczna jest nachylona do płaszczyzny podstawy pod kątem 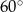 . Oblicz objętość ostrosłupa.
. Oblicz objętość ostrosłupa.
Trójkąt równoboczny 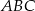 jest podstawą ostrosłupa prawidłowego
jest podstawą ostrosłupa prawidłowego 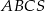 , w którym ściana boczna jest nachylona do płaszczyzny podstawy pod kątem
, w którym ściana boczna jest nachylona do płaszczyzny podstawy pod kątem 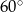 , a krawędź boczna ma długość
, a krawędź boczna ma długość 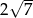 (zobacz rysunek). Oblicz objętość tego ostrosłupa.
(zobacz rysunek). Oblicz objętość tego ostrosłupa.
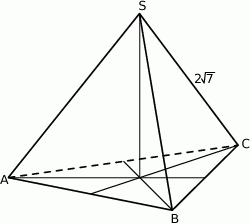
Trójkąt równoboczny 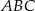 jest podstawą ostrosłupa prawidłowego
jest podstawą ostrosłupa prawidłowego 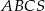 , w którym ściana boczna jest nachylona do płaszczyzny podstawy pod kątem
, w którym ściana boczna jest nachylona do płaszczyzny podstawy pod kątem 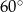 , a krawędź boczna ma długość 7 (zobacz rysunek). Oblicz objętość tego ostrosłupa.
, a krawędź boczna ma długość 7 (zobacz rysunek). Oblicz objętość tego ostrosłupa.