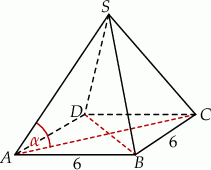
Długość krawędzi podstawy ostrosłupa prawidłowego czworokątnego jest równa 6. Pole powierzchni całkowitej tego ostrosłupa jest cztery razy większe od pola jego podstawy. Kąt  jest kątem nachylenia krawędzi bocznej tego ostrosłupa do płaszczyzny podstawy (zobacz rysunek). Oblicz cosinus kąta
jest kątem nachylenia krawędzi bocznej tego ostrosłupa do płaszczyzny podstawy (zobacz rysunek). Oblicz cosinus kąta  .
.

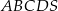 o podstawie
o podstawie 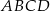 . Krawędź podstawy tego ostrosłupa ma długość
. Krawędź podstawy tego ostrosłupa ma długość  . Ściana boczna jest nachylona do płaszczyzny podstawy pod kątem o mierze
. Ściana boczna jest nachylona do płaszczyzny podstawy pod kątem o mierze  takim, że
takim, że 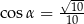 . Przez krawędź
. Przez krawędź 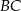 podstawy ostrosłupa poprowadzono płaszczyznę
podstawy ostrosłupa poprowadzono płaszczyznę 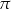 prostopadłą do ściany bocznej
prostopadłą do ściany bocznej 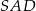 . Sporządź rysunek tego ostrosłupa, zaznacz na rysunku przekrój wyznaczony przez płaszczyznę
. Sporządź rysunek tego ostrosłupa, zaznacz na rysunku przekrój wyznaczony przez płaszczyznę 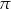 i nazwij figurę, która jest tym przekrojem. Oblicz pole otrzymanego przekroju.
i nazwij figurę, która jest tym przekrojem. Oblicz pole otrzymanego przekroju. 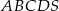 o podstawie
o podstawie 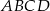 jest równa 224, a promień okręgu opisanego na podstawie
jest równa 224, a promień okręgu opisanego na podstawie 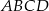 jest równy
jest równy 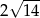 . Oblicz cosinus kąta między wysokością tego ostrosłupa i jego ścianą boczną.
. Oblicz cosinus kąta między wysokością tego ostrosłupa i jego ścianą boczną. 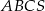 jest trójkąt
jest trójkąt 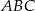 o bokach długości 18 cm i 12 cm, którego kąt między tymi bokami ma miarę równą
o bokach długości 18 cm i 12 cm, którego kąt między tymi bokami ma miarę równą 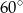 . Wszystkie krawędzie boczne ostrosłupa
. Wszystkie krawędzie boczne ostrosłupa 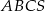 mają długości równe 12 cm. Ostrosłup ten przecięto płaszczyzną równoległą do podstawy i dzielącą jego wysokość w stosunku 1:2, licząc od wierzchołka tego ostrosłupa. Wykonaj rysunek ostrosłupa
mają długości równe 12 cm. Ostrosłup ten przecięto płaszczyzną równoległą do podstawy i dzielącą jego wysokość w stosunku 1:2, licząc od wierzchołka tego ostrosłupa. Wykonaj rysunek ostrosłupa 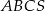 z zaznaczonym przekrojem i oblicz:
z zaznaczonym przekrojem i oblicz: 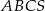 .
.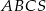 jest równa
jest równa 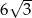 , a krawędź boczna tworzy z płaszczyzną podstawy kąt
, a krawędź boczna tworzy z płaszczyzną podstawy kąt 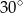 . Oblicz pole powierzchni bocznej tego ostrosłupa.
. Oblicz pole powierzchni bocznej tego ostrosłupa. 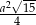 , gdzie
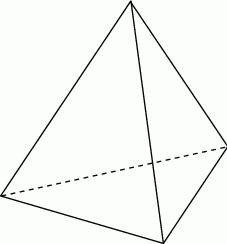
, gdzie  oznacza długość krawędzi podstawy tego ostrosłupa. Zaznacz na poniższym rysunku kąt nachylenia ściany bocznej ostrosłupa do płaszczyzny jego podstawy. Miarę tego kąta oznacz symbolem
oznacza długość krawędzi podstawy tego ostrosłupa. Zaznacz na poniższym rysunku kąt nachylenia ściany bocznej ostrosłupa do płaszczyzny jego podstawy. Miarę tego kąta oznacz symbolem 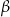 . Oblicz
. Oblicz 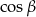 i korzystając z tablic funkcji trygonometrycznych i odczytaj przybliżoną wartość
i korzystając z tablic funkcji trygonometrycznych i odczytaj przybliżoną wartość 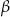 z dokładnością do
z dokładnością do 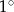 .
. 
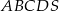 o podstawie
o podstawie 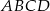 . Pole trójkąta
. Pole trójkąta 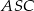 jest równe 120, a cosinus kąta
jest równe 120, a cosinus kąta 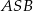 jest równy
jest równy 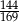 . Oblicz pole powierzchni bocznej tego ostrosłupa.
. Oblicz pole powierzchni bocznej tego ostrosłupa.  i jest 4 razy większa niż odległość środka podstawy od ściany bocznej. Oblicz objętość tego ostrosłupa.
i jest 4 razy większa niż odległość środka podstawy od ściany bocznej. Oblicz objętość tego ostrosłupa. 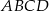 jest trójkąt
jest trójkąt 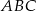 . Krawędź
. Krawędź 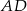 jest wysokością ostrosłupa (zobacz rysunek).
jest wysokością ostrosłupa (zobacz rysunek). 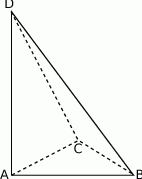
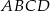 , jeśli wiadomo, że
, jeśli wiadomo, że 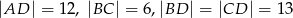 .
. 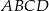 jest trójkąt
jest trójkąt 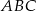 . Krawędź
. Krawędź 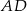 jest wysokością ostrosłupa (zobacz rysunek).
jest wysokością ostrosłupa (zobacz rysunek). 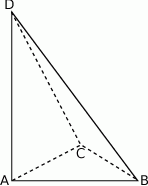
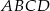 , jeśli wiadomo, że
, jeśli wiadomo, że 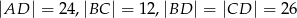 .
. 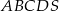 o podstawie
o podstawie 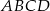 . W trójkącie równoramiennym
. W trójkącie równoramiennym 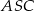 stosunek długości podstawy do długości ramienia jest równy
stosunek długości podstawy do długości ramienia jest równy 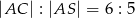 . Oblicz sinus kąta nachylenia ściany bocznej do płaszczyzny podstawy.
. Oblicz sinus kąta nachylenia ściany bocznej do płaszczyzny podstawy. 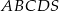 jest prostokąt
jest prostokąt 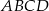 o bokach długości
o bokach długości 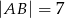 i
i 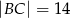 . Krawędź
. Krawędź 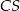 jest prostopadła do podstawy. Najdłuższa krawędź boczna tworzy z podstawą kąt
jest prostopadła do podstawy. Najdłuższa krawędź boczna tworzy z podstawą kąt 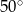 . Wykonaj rysunek pomocniczy tego ostrosłupa oraz oblicz jego objętość.
. Wykonaj rysunek pomocniczy tego ostrosłupa oraz oblicz jego objętość. 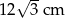 , a spodek
, a spodek 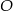 tej wysokości jest punktem przecięcia przekątnych. Każda ze ścian bocznych ostrosłupa tworzy z płaszczyzną podstawy kąt o mierze
tej wysokości jest punktem przecięcia przekątnych. Każda ze ścian bocznych ostrosłupa tworzy z płaszczyzną podstawy kąt o mierze 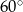 .
. 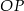 , którego długość jest równa odległości punktu
, którego długość jest równa odległości punktu 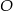 od ściany bocznej.
od ściany bocznej. 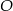 od ściany bocznej.
od ściany bocznej.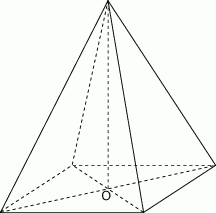
 . Ściana boczna ostrosłupa nachylona jest do płaszczyzny podstawy pod kątem
. Ściana boczna ostrosłupa nachylona jest do płaszczyzny podstawy pod kątem 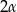 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.  .
.  .
. 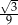 . Oblicz pole powierzchni bocznej tego ostrosłupa.
. Oblicz pole powierzchni bocznej tego ostrosłupa. 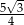 , a pole powierzchni bocznej tego ostrosłupa jest równe
, a pole powierzchni bocznej tego ostrosłupa jest równe 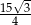 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa. 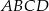 o boku długości 40. Pola ścian bocznych
o boku długości 40. Pola ścian bocznych 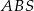 ,
, 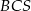 ,
, 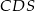 i
i 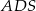 są odpowiednio równe: 740,
są odpowiednio równe: 740, 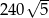 , 260 i 400. Oblicz objętość tego ostrosłupa.
, 260 i 400. Oblicz objętość tego ostrosłupa. 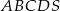 jest kwadrat
jest kwadrat 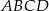 o boku długości 4. Odcinek
o boku długości 4. Odcinek 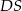 jest wysokością ostrosłupa i ma długość 6. Punkt
jest wysokością ostrosłupa i ma długość 6. Punkt 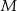 jest środkiem odcinka
jest środkiem odcinka 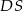 . Oblicz pole przekroju ostrosłupa płaszczyzną
. Oblicz pole przekroju ostrosłupa płaszczyzną 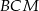 .
. 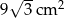 , a jego pole powierzchni bocznej jest równe
, a jego pole powierzchni bocznej jest równe 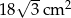 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa. 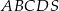 jest trapez prostokątny, w którym jedna z podstaw ma długość 7, a jedna z przekątnych ma długość
jest trapez prostokątny, w którym jedna z podstaw ma długość 7, a jedna z przekątnych ma długość 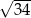 . Krawędź
. Krawędź 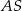 jest wysokością ostrosłupa oraz
jest wysokością ostrosłupa oraz 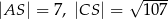 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa. 