Podstawą ostrosłupa 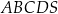 jest kwadrat
jest kwadrat 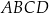 (patrz rysunek).
(patrz rysunek).
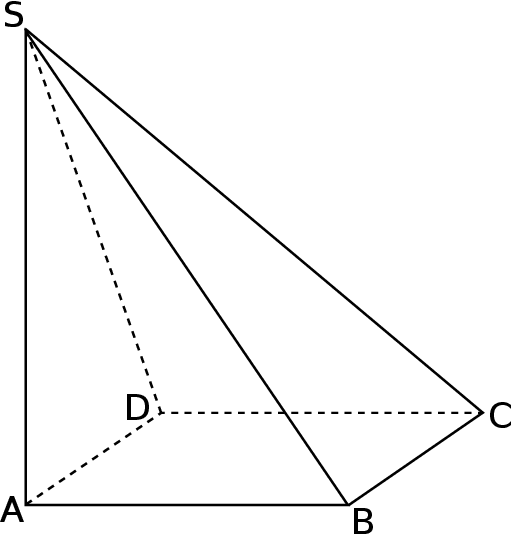
Krawędź 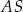 jest wysokością tego ostrosłupa. Odległość punktu
jest wysokością tego ostrosłupa. Odległość punktu 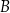 od krawędzi
od krawędzi 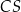 jest równa
jest równa 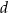 , a kąt dwuścienny między ścianami
, a kąt dwuścienny między ścianami 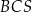 i
i 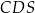 ma miarę
ma miarę 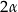 , gdzie
, gdzie 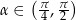 . Oblicz:
. Oblicz:
-
odległość punktu
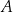 od krawędzi
od krawędzi 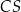
-
wysokość tego ostrosłupa.

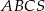 podstawa
podstawa 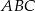 jest trójkątem prostokątnym,
jest trójkątem prostokątnym, 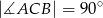 . Sinus jednego z kątów ostrych podstawy jest równy 0,6 . Promień okręgu opisanego na podstawie ma długość 10 cm. Wysokość
. Sinus jednego z kątów ostrych podstawy jest równy 0,6 . Promień okręgu opisanego na podstawie ma długość 10 cm. Wysokość 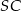 ostrosłupa ma długość 24 cm. Oblicz:
ostrosłupa ma długość 24 cm. Oblicz: 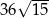 .
.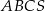 jest trójkąt równoboczny
jest trójkąt równoboczny 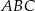 o boku długości 6. Na krawędziach bocznych
o boku długości 6. Na krawędziach bocznych 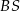 i
i 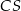 wybrano punkty, odpowiednio
wybrano punkty, odpowiednio 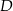 i
i 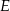 , takie że
, takie że 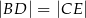 oraz
oraz 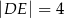 (zobacz rysunek). Płaszczyzna
(zobacz rysunek). Płaszczyzna 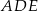 jest prostopadła do płaszczyzny ściany bocznej
jest prostopadła do płaszczyzny ściany bocznej 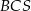 ostrosłupa.
ostrosłupa. 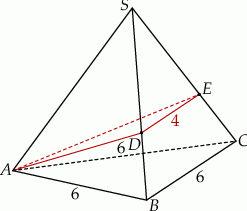
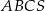 jest trójkąt równoboczny
jest trójkąt równoboczny 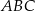 o boku długości 8. Na krawędziach bocznych
o boku długości 8. Na krawędziach bocznych 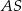 i
i 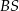 wybrano punkty, odpowiednio
wybrano punkty, odpowiednio 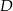 i
i 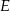 , takie że
, takie że 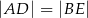 oraz
oraz 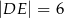 (zobacz rysunek). Płaszczyzna
(zobacz rysunek). Płaszczyzna 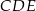 jest prostopadła do płaszczyzny ściany bocznej
jest prostopadła do płaszczyzny ściany bocznej 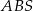 ostrosłupa.
ostrosłupa. 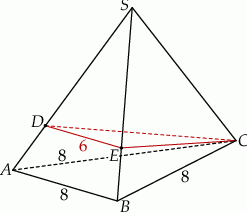
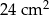 . Każda krawędź boczna jest nachylona do płaszczyzny podstawy pod kątem
. Każda krawędź boczna jest nachylona do płaszczyzny podstawy pod kątem 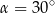 . Oblicz pole powierzchni bocznej tego ostrosłupa.
. Oblicz pole powierzchni bocznej tego ostrosłupa. 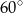 . Oblicz pole powierzchni bocznej tego ostrosłupa.
. Oblicz pole powierzchni bocznej tego ostrosłupa.  . Kąt między krawędzią boczną i krawędzią podstawy ma miarę
. Kąt między krawędzią boczną i krawędzią podstawy ma miarę 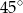 . Ostrosłup przecięto płaszczyzną przechodzącą przez krawędź podstawy i środek przeciwległej jej krawędzi bocznej. Sporządź rysunek ostrosłupa i zaznacz otrzymany przekrój. Oblicz pole tego przekroju.
. Ostrosłup przecięto płaszczyzną przechodzącą przez krawędź podstawy i środek przeciwległej jej krawędzi bocznej. Sporządź rysunek ostrosłupa i zaznacz otrzymany przekrój. Oblicz pole tego przekroju.  . Kąt między krawędzią boczną i krawędzią podstawy ma miarę
. Kąt między krawędzią boczną i krawędzią podstawy ma miarę 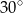 . Ostrosłup przecięto płaszczyzną przechodzącą przez krawędź podstawy i środek przeciwległej jej krawędzi bocznej. Sporządź rysunek ostrosłupa i zaznacz otrzymany przekrój. Oblicz pole tego przekroju.
. Ostrosłup przecięto płaszczyzną przechodzącą przez krawędź podstawy i środek przeciwległej jej krawędzi bocznej. Sporządź rysunek ostrosłupa i zaznacz otrzymany przekrój. Oblicz pole tego przekroju. 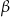 . Wszystkie krawędzie boczne mają długość
. Wszystkie krawędzie boczne mają długość 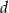 i są nachylone do płaszczyzny podstawy pod kątem o mierze
i są nachylone do płaszczyzny podstawy pod kątem o mierze  . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa. 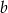 , a kąt nachylenia krawędzi bocznej, przechodzącej przez wierzchołek wspólny równych krawędzi podstawy, do płaszczyzny podstawy ma miarę
, a kąt nachylenia krawędzi bocznej, przechodzącej przez wierzchołek wspólny równych krawędzi podstawy, do płaszczyzny podstawy ma miarę  . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa. 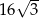 , a jego objętość
, a jego objętość 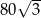 . Wyznacz cosinus kąta
. Wyznacz cosinus kąta  nachylenia ściany bocznej do płaszczyzny podstawy.
nachylenia ściany bocznej do płaszczyzny podstawy. 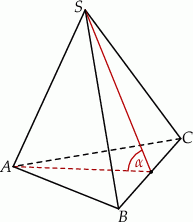
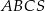 (tak jak na rysunku) jest równa 72, a promień okręgu wpisanego w podstawę
(tak jak na rysunku) jest równa 72, a promień okręgu wpisanego w podstawę  tego ostrosłupa jest równy 2. Oblicz tangens kąta między wysokością tego ostrosłupa i jego ścianą boczną.
tego ostrosłupa jest równy 2. Oblicz tangens kąta między wysokością tego ostrosłupa i jego ścianą boczną. 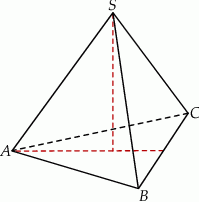
 (patrz rysunek) jest równa 36, a promień okręgu opisanego na podstawie
(patrz rysunek) jest równa 36, a promień okręgu opisanego na podstawie  tego ostrosłupa jest równy 2. Oblicz tangens kąta jaki tworzy krawędź boczna z wysokością ostrosłupa.
tego ostrosłupa jest równy 2. Oblicz tangens kąta jaki tworzy krawędź boczna z wysokością ostrosłupa. 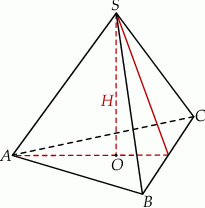
 (patrz rysunek) jest równa 36, a promień okręgu opisanego na podstawie
(patrz rysunek) jest równa 36, a promień okręgu opisanego na podstawie 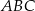 tego ostrosłupa jest równy 4. Oblicz tangens kąta jaki tworzy krawędź boczna z wysokością ostrosłupa.
tego ostrosłupa jest równy 4. Oblicz tangens kąta jaki tworzy krawędź boczna z wysokością ostrosłupa. 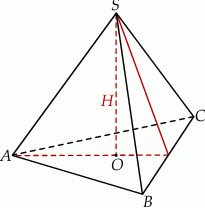
 (tak jak na rysunku) jest równa 243, a promień okręgu wpisanego w podstawę
(tak jak na rysunku) jest równa 243, a promień okręgu wpisanego w podstawę 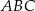 tego ostrosłupa jest równy 3. Oblicz tangens kąta między wysokością tego ostrosłupa, a jego krawędzią boczną.
tego ostrosłupa jest równy 3. Oblicz tangens kąta między wysokością tego ostrosłupa, a jego krawędzią boczną. 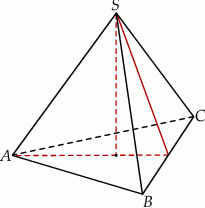
 i przeciwprostokątnej długości
i przeciwprostokątnej długości  . Wszystkie ściany boczne ostrosłupa są nachylone do płaszczyzny podstawy pod kątem
. Wszystkie ściany boczne ostrosłupa są nachylone do płaszczyzny podstawy pod kątem 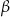 . Wykaż, że pole powierzchni całkowitej tego ostrosłupa jest równe
. Wykaż, że pole powierzchni całkowitej tego ostrosłupa jest równe 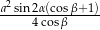 .
. 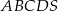 jest kwadrat
jest kwadrat 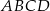 . Krawędź boczna
. Krawędź boczna 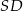 jest wysokością ostrosłupa, a jej długość jest dwa razy większa od długości krawędzi podstawy. Oblicz sinus kąta między ścianami bocznymi
jest wysokością ostrosłupa, a jej długość jest dwa razy większa od długości krawędzi podstawy. Oblicz sinus kąta między ścianami bocznymi 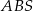 i
i 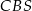 tego ostrosłupa.
tego ostrosłupa. 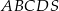 jest kwadrat
jest kwadrat 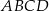 o boku długości
o boku długości  , a krawędź boczna
, a krawędź boczna 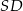 jest wysokością ostrosłupa. Oblicz objętość ostrosłupa jeżeli cosinus kąta między ścianami bocznymi
jest wysokością ostrosłupa. Oblicz objętość ostrosłupa jeżeli cosinus kąta między ścianami bocznymi 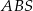 i
i 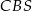 tego ostrosłupa jest równy
tego ostrosłupa jest równy 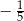 .
. 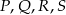 są środkami odpowiednio krawędzi
są środkami odpowiednio krawędzi 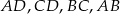 czworościanu
czworościanu 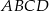 . Wykaż, że punkty
. Wykaż, że punkty 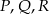 i
i 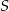 są wierzchołkami równoległoboku.
są wierzchołkami równoległoboku. 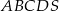 jest romb
jest romb 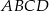 , w którym
, w którym 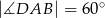 . Krawędź
. Krawędź 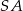 jest wysokością ostrosłupa oraz jej długość jest równa długości krawędzi podstawy. Oblicz sinus kąta nachylenia ściany
jest wysokością ostrosłupa oraz jej długość jest równa długości krawędzi podstawy. Oblicz sinus kąta nachylenia ściany 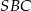 do płaszczyzny podstawy.
do płaszczyzny podstawy. 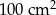 , a jego pole powierzchni bocznej jest równe
, a jego pole powierzchni bocznej jest równe 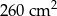 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa. 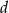 . Krawędź boczna tworzy z płaszczyzną podstawy kąt
. Krawędź boczna tworzy z płaszczyzną podstawy kąt  . Oblicz objętość i pole powierzchni całkowitej ostrosłupa.
. Oblicz objętość i pole powierzchni całkowitej ostrosłupa. 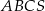 płaszczyzną przechodzącą przez wierzchołek
płaszczyzną przechodzącą przez wierzchołek 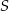 i wysokości dwóch ścian bocznych jest trójkątem równobocznym. Krawędź boczna tego ostrosłupa ma długość
i wysokości dwóch ścian bocznych jest trójkątem równobocznym. Krawędź boczna tego ostrosłupa ma długość 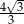 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa. 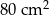 , a pole jego powierzchni całkowitej wynosi
, a pole jego powierzchni całkowitej wynosi 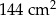 . Oblicz długość krawędzi podstawy i długość krawędzi bocznej tego ostrosłupa. Zapisz obliczenia.
. Oblicz długość krawędzi podstawy i długość krawędzi bocznej tego ostrosłupa. Zapisz obliczenia. 