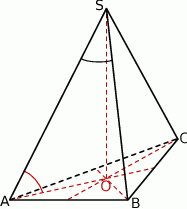
Wysokość ostrosłupa prawidłowego czworokątnego jest równa 8. Krawędź boczna jest nachylona do płaszczyzny podstawy pod kątem 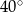 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
/Szkoła średnia/Geometria/Stereometria/Ostrosłup
Wysokość ostrosłupa prawidłowego czworokątnego jest równa 6. Krawędź boczna jest nachylona do płaszczyzny podstawy pod kątem 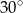 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
Podstawą ostrosłupa 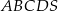 jest trapez
jest trapez 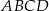 . Przekątna
. Przekątna 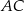 tego trapezu ma długość
tego trapezu ma długość 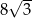 , jest prostopadła do ramienia
, jest prostopadła do ramienia 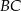 i tworzy z dłuższą podstawą
i tworzy z dłuższą podstawą 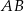 tego trapezu kąt o mierze
tego trapezu kąt o mierze 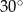 . Każda krawędź boczna tego ostrosłupa ma tę samą długość
. Każda krawędź boczna tego ostrosłupa ma tę samą długość 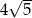 . Oblicz odległość spodka wysokości tego ostrosłupa od jego krawędzi bocznej
. Oblicz odległość spodka wysokości tego ostrosłupa od jego krawędzi bocznej 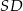 .
.
Podstawą ostrosłupa 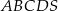 jest trapez
jest trapez 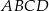 . Przekątna
. Przekątna 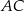 tego trapezu ma długość
tego trapezu ma długość 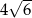 , jest prostopadła do ramienia
, jest prostopadła do ramienia 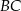 i tworzy z dłuższą podstawą
i tworzy z dłuższą podstawą 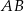 tego trapezu kąt o mierze
tego trapezu kąt o mierze 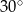 . Każda krawędź boczna tego ostrosłupa ma tę samą długość 9. Oblicz odległość spodka wysokości tego ostrosłupa od jego krawędzi bocznej
. Każda krawędź boczna tego ostrosłupa ma tę samą długość 9. Oblicz odległość spodka wysokości tego ostrosłupa od jego krawędzi bocznej 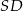 .
.
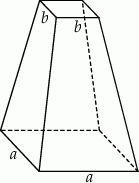
Przedstawiona na rysunku bryła to ostrosłup prawidłowy czworokątny ścięty płaszczyzną równoległą do jego płaszczyzny podstawy. Wysokość tej bryły jest równa 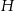 , a
, a  i
i 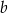 (
( ) są długościami krawędzi jego podstaw. Oblicz objętość tej bryły.
) są długościami krawędzi jego podstaw. Oblicz objętość tej bryły.
Podstawą ostrosłupa 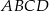 jest trójkąt
jest trójkąt 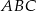 . Krawędź
. Krawędź 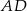 jest wysokością ostrosłupa (zobacz rysunek).
jest wysokością ostrosłupa (zobacz rysunek).
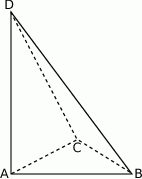
Oblicz objętość ostrosłupa 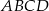 , jeśli wiadomo, że
, jeśli wiadomo, że 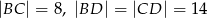 oraz pole podstawy jest równe 24.
oraz pole podstawy jest równe 24.
Pole przekroju ostrosłupa prawidłowego czworokątnego płaszczyzną przechodzącą przez przekątną podstawy i równoległą do krawędzi bocznej rozłącznej z tą przekątną wynosi  . Oblicz pole przekroju ostrosłupa płaszczyzną zawierającą środki dwóch sąsiednich boków podstawy i środek wysokości ostrosłupa.
. Oblicz pole przekroju ostrosłupa płaszczyzną zawierającą środki dwóch sąsiednich boków podstawy i środek wysokości ostrosłupa.
Podstawą ostrosłupa jest trójkąt, którego jeden bok ma długość 4, a kąty przyległe do tego boku mają miary 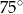 i
i 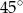 . Wysokość ostrosłupa ma długość równą długości promienia koła opisanego na podstawie. Oblicz objętość ostrosłupa. Wynik podaj w postaci
. Wysokość ostrosłupa ma długość równą długości promienia koła opisanego na podstawie. Oblicz objętość ostrosłupa. Wynik podaj w postaci 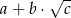 , gdzie
, gdzie  ,
, 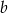 ,
,  są liczbami wymiernymi.
są liczbami wymiernymi.
Podstawą ostrosłupa jest trójkąt, którego jeden z boków ma długość 6, a kąty przyległe do niego mają miary 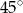 i
i 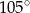 . Wysokość ostrosłupa ma długość równą długości promienia okręgu opisanego na podstawie. Oblicz objętość ostrosłupa. Wynik podaj w postaci
. Wysokość ostrosłupa ma długość równą długości promienia okręgu opisanego na podstawie. Oblicz objętość ostrosłupa. Wynik podaj w postaci 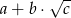 , gdzie
, gdzie  ,
, 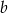 ,
,  są liczbami wymiernymi.
są liczbami wymiernymi.
Długość krawędzi bocznej ostrosłupa prawidłowego trójkątnego 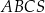 jest równa
jest równa 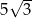 (zobacz rysunek). Krawędź boczna tworzy z wysokością tego ostrosłupa kąt
(zobacz rysunek). Krawędź boczna tworzy z wysokością tego ostrosłupa kąt  taki, że
taki, że 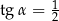 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
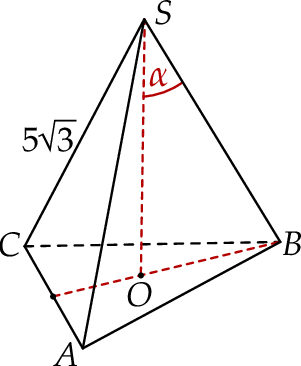
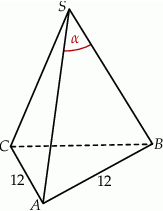
W ostrosłupie prawidłowym trójkątnym  krawędź podstawy ma długość 12, a jego objętość jest równa
krawędź podstawy ma długość 12, a jego objętość jest równa 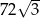 . Kąt
. Kąt  jest kątem między krawędziami bocznymi
jest kątem między krawędziami bocznymi 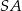 i
i 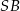 (zobacz rysunek). Oblicz sinus kąta
(zobacz rysunek). Oblicz sinus kąta  .
.
W ostrosłupie prawidłowym czworokątnym dane są:  – wysokość ostrosłupa oraz
– wysokość ostrosłupa oraz  — miara kąta utworzonego przez krawędź boczną i krawędź podstawy (
— miara kąta utworzonego przez krawędź boczną i krawędź podstawy (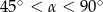 ).
).
- Wykaż, że objętość
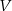 tego ostrosłupa jest równa
tego ostrosłupa jest równa 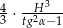 .
. - Oblicz miarę kąta
 , dla której objętość
, dla której objętość 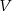 danego ostrosłupa jest równa
danego ostrosłupa jest równa 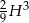 . Wynik podaj w zaookrągleniu do całkowitej liczby stopni.
. Wynik podaj w zaookrągleniu do całkowitej liczby stopni.
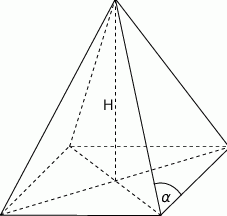
Przekrój ostrosłupa prawidłowego czworokątnego zawierającego przekątną podstawy oraz wierzchołek ostrosłupa jest trójkątem równobocznym o polu 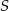 . Oblicz objętość tego ostrosłupa . Wykonaj rysunek pomocniczy.
. Oblicz objętość tego ostrosłupa . Wykonaj rysunek pomocniczy.
Ostrosłup 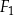 jest podobny do ostrosłupa
jest podobny do ostrosłupa 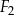 . Objętość ostrosłupa
. Objętość ostrosłupa 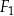 jest równa 64, a objętość ostrosłupa
jest równa 64, a objętość ostrosłupa 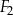 jest równa 512. Oblicz stosunek pola powierzchni całkowitej ostrosłupa
jest równa 512. Oblicz stosunek pola powierzchni całkowitej ostrosłupa 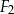 do pola powierzchni całkowitej ostrosłupa
do pola powierzchni całkowitej ostrosłupa 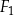 .
.
Podstawą ostrosłupa 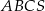 jest trójkąt
jest trójkąt 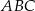 , w którym
, w którym 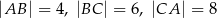 . Wszystkie ściany boczne tworzą z płaszczyzną podstawy kąt
. Wszystkie ściany boczne tworzą z płaszczyzną podstawy kąt 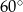 . Oblicz objętość ostrosłupa.
. Oblicz objętość ostrosłupa.
Podstawą ostrosłupa prawidłowego trójkątnego 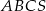 jest trójkąt
jest trójkąt 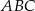 . Punkty
. Punkty 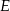 i
i 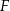 są rzutami punktów
są rzutami punktów 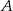 i
i 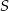 na przeciwległe ściany. Oblicz w jakim stosunku odcinek
na przeciwległe ściany. Oblicz w jakim stosunku odcinek 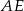 dzieli odcinek
dzieli odcinek 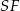 , jeżeli ściana boczna ostrosłupa jest nachylona do podstawy pod kątem, którego sinus jest równy
, jeżeli ściana boczna ostrosłupa jest nachylona do podstawy pod kątem, którego sinus jest równy  .
.
Podstawą ostrosłupa 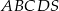 jest prostokąt
jest prostokąt 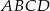 . Spodkiem wysokości ostrosłupa jest środek
. Spodkiem wysokości ostrosłupa jest środek 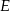 krawędzi
krawędzi 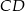 . Oblicz tangens kąta między ścianami bocznymi
. Oblicz tangens kąta między ścianami bocznymi 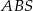 i
i 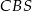 tego ostrosłupa jeżeli
tego ostrosłupa jeżeli 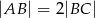 i
i 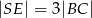 .
.
W ostrosłupie prawidłowym czworokątnym ściana boczna o polu równym 10 jest nachylona do płaszczyzny podstawy pod kątem 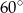 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
Podstawą ostrosłupa 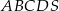 jest trapez równoramienny
jest trapez równoramienny 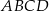 , którego ramiona mają długość
, którego ramiona mają długość 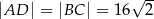 i tworzą z podstawą
i tworzą z podstawą 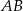 kąt ostry o mierze
kąt ostry o mierze 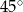 . Każda ściana boczna tego ostrosłupa jest nachylona do płaszczyzny podstawy pod tym samym kątem
. Każda ściana boczna tego ostrosłupa jest nachylona do płaszczyzny podstawy pod tym samym kątem  takim, że
takim, że 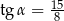 . Oblicz odległość spodka wysokości tego ostrosłupa od jego ściany bocznej
. Oblicz odległość spodka wysokości tego ostrosłupa od jego ściany bocznej 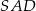 .
.
Podstawą ostrosłupa czworokątnego 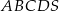 jest trapez
jest trapez 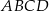 (
(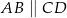 ). Ramiona tego trapezu mają długości
). Ramiona tego trapezu mają długości 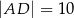 i
i 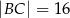 , a miara kąta
, a miara kąta 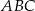 jest równa
jest równa 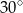 . Każda ściana boczna tego ostrosłupa tworzy z płaszczyzną podstawy kąt
. Każda ściana boczna tego ostrosłupa tworzy z płaszczyzną podstawy kąt  , taki, że
, taki, że 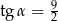 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
Oblicz objętość i pole powierzchni całkowitej ostrosłupa prawidłowego czworokątnego, w którym krawędź podstawy ma długość 2, a krawędź boczna długość 6.
Oblicz objętość i pole powierzchni całkowitej ostrosłupa prawidłowego czworokątnego, w którym krawędź boczna ma długość 8, a krawędź podstawy ma długość 2.
Oblicz objętość i pole powierzchni całkowitej ostrosłupa prawidłowego czworokątnego, w którym krawędź podstawy ma długość 4, a krawędź boczna długość 10.
W ostrosłupie prawidłowym czworokątnym 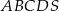 o podstawie
o podstawie 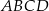 wysokość jest równa 5, a kąt między sąsiednimi ścianami bocznymi ostrosłupa ma miarę
wysokość jest równa 5, a kąt między sąsiednimi ścianami bocznymi ostrosłupa ma miarę 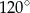 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
Dany jest ostrosłup prawidłowy czworokątny. Wysokość ściany bocznej tego ostrosłupa jest nachylona do płaszczyzny podstawy pod kątem 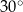 i ma długość równą 6 (zobacz rysunek).
i ma długość równą 6 (zobacz rysunek).
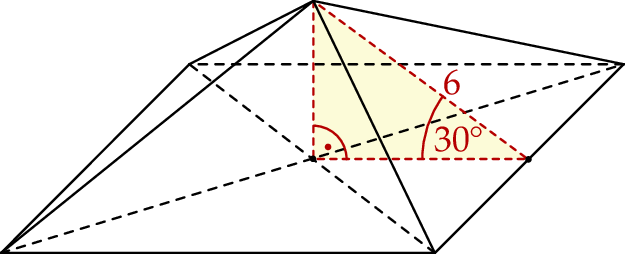
Oblicz objętość i pole powierzchni całkowitej tego ostrosłupa.
Dany jest ostrosłup prawidłowy czworokątny. Wysokość ściany bocznej tego ostrosłupa jest nachylona do płaszczyzny podstawy pod kątem 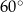 i ma długość równą 6 (zobacz rysunek).
i ma długość równą 6 (zobacz rysunek).
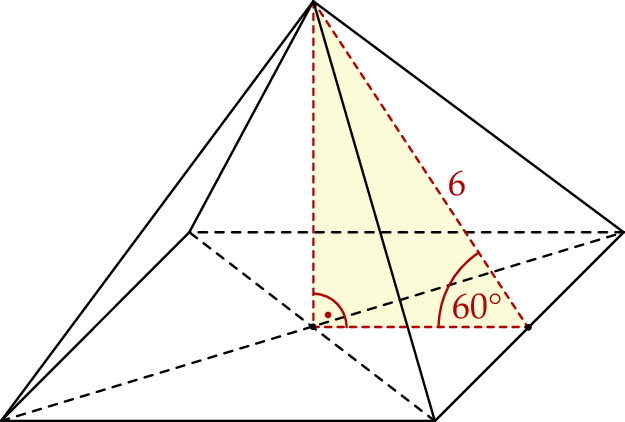
Oblicz objętość i pole powierzchni całkowitej tego ostrosłupa.
Dany jest ostrosłup prawidłowy czworokątny. Ściana boczna tego ostrosłupa jest nachylona do płaszczyzny podstawy pod kątem 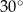 , a krawędź podstawy ma długość równą
, a krawędź podstawy ma długość równą 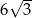 . Oblicz objętość i pole powierzchni całkowitej tego ostrosłupa.
. Oblicz objętość i pole powierzchni całkowitej tego ostrosłupa.
Podstawą ostrosłupa prawidłowego trójkątnego 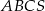 jest trójkąt
jest trójkąt 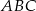 . Kąt nachylenia krawędzi bocznej
. Kąt nachylenia krawędzi bocznej 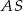 do płaszczyzny podstawy ostrosłupa jest równy kątowi między krawędziami bocznymi
do płaszczyzny podstawy ostrosłupa jest równy kątowi między krawędziami bocznymi 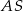 i
i 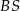 zawartymi w ścianie bocznej
zawartymi w ścianie bocznej 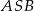 tego ostrosłupa (zob. rysunek). Oblicz kosinus tego kąta.
tego ostrosłupa (zob. rysunek). Oblicz kosinus tego kąta.