Objętość ostrosłupa prawidłowego trójkątnego 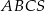 jest równa
jest równa 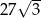 . Długość krawędzi
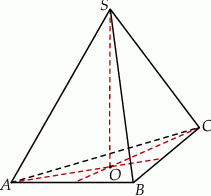
. Długość krawędzi 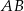 podstawy ostrosłupa jest równa 6 (zobacz rysunek). Oblicz pole powierzchni całkowitej tego ostrosłupa.
podstawy ostrosłupa jest równa 6 (zobacz rysunek). Oblicz pole powierzchni całkowitej tego ostrosłupa.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Objętość ostrosłupa prawidłowego trójkątnego 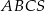 jest równa
jest równa 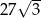 . Długość krawędzi
. Długość krawędzi 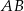 podstawy ostrosłupa jest równa 6 (zobacz rysunek). Oblicz pole powierzchni całkowitej tego ostrosłupa.
podstawy ostrosłupa jest równa 6 (zobacz rysunek). Oblicz pole powierzchni całkowitej tego ostrosłupa.

Objętość ostrosłupa prawidłowego trójkątnego 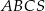 jest równa
jest równa 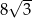 . Długość krawędzi
. Długość krawędzi 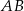 podstawy ostrosłupa jest równa 4 (zobacz rysunek). Oblicz pole powierzchni całkowitej tego ostrosłupa.
podstawy ostrosłupa jest równa 4 (zobacz rysunek). Oblicz pole powierzchni całkowitej tego ostrosłupa.
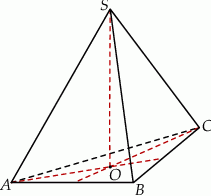
Podstawą ostrosłupa jest trójkąt równoramienny o ramieniu długości 10 i podstawie długości 12. Wszystkie krawędzie boczne ostrosłupa mają długość 7. Oblicz objętość i pole powierzchni bocznej tego ostrosłupa.
Podstawą ostrosłupa o objętości 30 jest trójkąt równoramienny o ramieniu długości 5 i podstawie długości 6. Oblicz pole powierzchni bocznej ostrosłupa wiedząc, że wszystkie krawędzie boczne mają jednakową długość.
Trójkąt 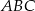 jest podstawą prawidłowego ostrosłupa
jest podstawą prawidłowego ostrosłupa 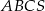 , którego krawędź boczna ma długość 10. Punkt
, którego krawędź boczna ma długość 10. Punkt 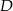 jest środkiem wysokości
jest środkiem wysokości 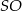 ostrosłupa oraz
ostrosłupa oraz 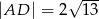 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
Oblicz cosinus kąta między ścianą boczną i płaszczyzną podstawy ostrosłupa prawidłowego trójkątnego, jeżeli wiadomo, że promień okręgu opisanego na podstawie, wysokość ostrosłupa i krawędź boczna tworzą trójkąt równoramienny.
Oblicz cosinus kąta między krawędzią boczną i krawędzią podstawy ostrosłupa prawidłowego trójkątnego, jeżeli wiadomo, że promień okręgu opisanego na podstawie, wysokość ostrosłupa i krawędź boczna tworzą trójkąt równoramienny.
W ostrosłupie prawidłowym trójkątnym krawędź boczna ma długość 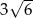 , a krawędź podstawy ma długość 12. Oblicz miarę kąta utworzonego przez dwie sąsiednie ściany boczne.
, a krawędź podstawy ma długość 12. Oblicz miarę kąta utworzonego przez dwie sąsiednie ściany boczne.
Podstawą ostrosłupa 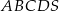 jest równoległobok
jest równoległobok 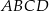 o przekątnej długości
o przekątnej długości 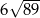 i bokach długości 32 i 34. Pole powierzchni bocznej jednej ze ścian bocznych ostrosłupa jest mniejsze od pola powierzchni sąsiedniej ściany bocznej i jest równe 1808. Spodek wysokości ostrosłupa pokrywa się z punktem przecięcia przekątnych równoległoboku
i bokach długości 32 i 34. Pole powierzchni bocznej jednej ze ścian bocznych ostrosłupa jest mniejsze od pola powierzchni sąsiedniej ściany bocznej i jest równe 1808. Spodek wysokości ostrosłupa pokrywa się z punktem przecięcia przekątnych równoległoboku 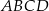 , a jego ściany boczne są trójkątami ostrokątnymi. Oblicz długość krótszej z krawędzi bocznych ostrosłupa
, a jego ściany boczne są trójkątami ostrokątnymi. Oblicz długość krótszej z krawędzi bocznych ostrosłupa 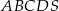 .
.
Podstawa ostrosłupa prawidłowego czworokątnego ma pole 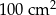 , a jego pole powierzchni bocznej jest równe
, a jego pole powierzchni bocznej jest równe 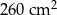 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
Wysokość ostrosłupa prawidłowego czworokątnego tworzy ze ścianą boczną kąt o mierze 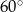 . Pole powierzchni bocznej ostrosłupa jest równe
. Pole powierzchni bocznej ostrosłupa jest równe 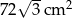 . Oblicz objętość ostrosłupa.
. Oblicz objętość ostrosłupa.
Dany jest ostrosłup, którego podstawą jest trójkąt równoboczny o boku 6. Jedna z krawędzi bocznych tego ostrosłupa ma długość 8 i jest prostopadła do płaszczyzny podstawy. Oblicz objętość tego ostrosłupa.
Podstawą ostrosłupa prawidłowego 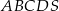 jest kwadrat
jest kwadrat 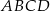 . Punkt
. Punkt 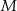 jest środkiem odcinka
jest środkiem odcinka 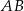 , a punkt
, a punkt 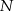 jest środkiem odcinka
jest środkiem odcinka 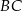 . Trójkąt
. Trójkąt 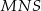 jest równoboczny i jego bok ma długość
jest równoboczny i jego bok ma długość 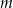 . Oblicz objętość ostrosłupa
. Oblicz objętość ostrosłupa 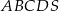 i kąt nachylenia ściany bocznej do płaszczyzny podstawy tego ostrosłupa.
i kąt nachylenia ściany bocznej do płaszczyzny podstawy tego ostrosłupa.
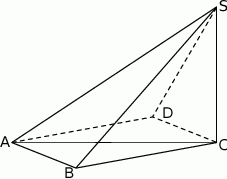
Podstawą ostrosłupa 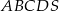 jest romb
jest romb 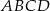 . Krawędź
. Krawędź 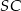 jest prostopadła do płaszczyzny podstawy, krawędź
jest prostopadła do płaszczyzny podstawy, krawędź 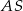 ma długość 4 i jest nachylona do płaszczyzny podstawy pod kątem
ma długość 4 i jest nachylona do płaszczyzny podstawy pod kątem 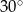 . Krawędź
. Krawędź 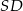 ma długość
ma długość 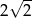 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
Wysokość prawidłowego ostrosłupa sześciokątnego ma długość 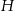 , a krawędź podstawy ma długość
, a krawędź podstawy ma długość  . Wyznacz pole przekroju wyznaczonego przez krótszą przekątną podstawy i wierzchołek ostrosłupa.
. Wyznacz pole przekroju wyznaczonego przez krótszą przekątną podstawy i wierzchołek ostrosłupa.
Oblicz wysokość i objętość ostrosłupa prawidłowego sześciokątnego o krawędzi podstawy 4 cm i krawędzi bocznej 10 cm.
Podstawą ostrosłupa jest prostokąt o polu 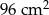 kwadratowych. Stosunek długości boków tego prostokąta wynosi 2:3. Krawędzie boczne ostrosłupa są nachylone do płaszczyzny podstawy pod kątem
kwadratowych. Stosunek długości boków tego prostokąta wynosi 2:3. Krawędzie boczne ostrosłupa są nachylone do płaszczyzny podstawy pod kątem 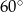 . Oblicz pole powierzchni całkowitej tej bryły.
. Oblicz pole powierzchni całkowitej tej bryły.
W ostrosłup prawidłowy czworokątny wpisano sześcian tak, że jego cztery wierzchołki należą do krawędzi bocznych ostrosłupa, a pozostałe do płaszczyzny podstawy. Oblicz długość krawędzi sześcianu, jeżeli wysokość ostrosłupa jest równa 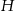 , a długość jego krawędzi podstawy jest równa
, a długość jego krawędzi podstawy jest równa  .
.
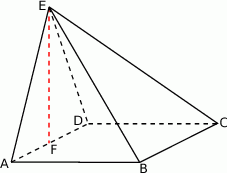
Podstawą ostrosłupa 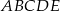 jest kwadrat
jest kwadrat 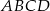 . Punkt
. Punkt 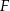 jest środkiem krawędzi
jest środkiem krawędzi 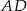 , odcinek
, odcinek 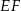 jest wysokością ostrosłupa. Oblicz objętość ostrosłupa, jeśli wiadomo, że
jest wysokością ostrosłupa. Oblicz objętość ostrosłupa, jeśli wiadomo, że 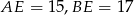 .
.
W ostrosłupie prawidłowym trójkątnym krawędzie boczne są dwa razy dłuższe od krawędzi podstawy.
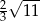 .
.Można przyjąć, że piramida Cheopsa jest ostrosłupem prawidłowym czworokątnym o krawędzi podstawy 233 m. Długość cienia piramidy w momencie, gdy promienie słoneczne padają prostopadle do jednej ze ścian wynosi 67,5 m. Wyznacz wysokość piramidy.
Oblicz objętość i pole powierzchni bocznej ostrosłupa prawidłowego sześciokątnego o krawędzi podstawy 2 cm i krawędzi bocznej 6 cm.
Krawędź boczna ostrosłupa prawidłowego czworokątnego ma długość 12 i jest nachylona do płaszczyzny podstawy pod kątem 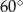 . Oblicz pole powierzchni całkowitej tego ostrosłupa.
. Oblicz pole powierzchni całkowitej tego ostrosłupa.
