Prawidłowy czworokątny - zadania z matematyki

/Szkoła średnia/Geometria/Stereometria/Ostrosłup/Prawidłowy czworokątny

Tangens kąta nachylenia ściany bocznej do płaszczyzny podstawy ostrosłupa prawidłowego czworokątnego jest równy . Oblicz tangens nachylenia krawędzi bocznej do płaszczyzny podstawy tego ostrosłupa.

W ostrosłupie prawidłowym czworokątnym 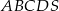ABCDS o podstawie 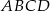ABCD i wierzchołku 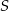trójkąt 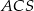ACS jest równoboczny i ma bok długości 8. Oblicz sinus kąta nachylenia ściany bocznej do płaszczyzny podstawy tego ostrosłupa (zobacz rysunek).

W ostrosłupie prawidłowym czworokątnym przeciwległe krawędzie boczne są prostopadłe, a wysokość ściany bocznej poprowadzona z wierzchołka ostrosłupa ma długość 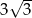√ -- 3 3 . Oblicz objętość i pole powierzchni całkowitej ostrosłupa.

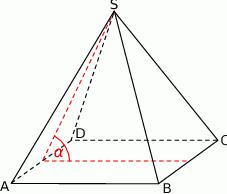
Podstawą ostrosłupa prawidłowego jest kwadrat o przekątnej 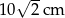√ -- 1 0 2 cm . Krawędź boczna ostrosłupa tworzy z podstawą kąt o mierze 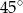45∘ . Oblicz pole powierzchni całkowitej i objętość tego ostrosłupa.

Dany jest ostrosłup prawidłowy czworokątny 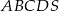ABCDS o podstawie 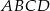ABCD . Pole trójkąta 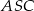ASC jest równe 120, a stosunek długości podstawy tego trójkąta do długości ramienia jest równy 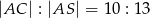|AC | : |AS | = 10 : 13 . Oblicz objętość i pole powierzchni bocznej tego ostrosłupa.

W ostrosłupie prawidłowym czworokątnym pole podstawy jest równe 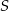, a kąt nachylenia ściany bocznej do płaszczyzny podstawy ma miarę . Ostrosłup przecięto płaszczyzną zawierającą krawędź boczną tego ostrosłupa i przechodzącą przez środek rozłącznej z nią krawędzi podstawy. Oblicz pole otrzymanego przekroju.

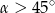W ostrosłupie prawidłowym czworokątnym krawędź podstawy ma długość . Kąt między krawędzią boczną, a krawędzią podstawy ma miarę α > 4 5∘ (zobacz rysunek). Oblicz objętość tego ostrosłupa.

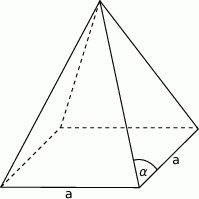
W ostrosłupie prawidłowym czworokątnym krawędź boczna ma długość 4 cm i jest nachylona do płaszczyzny podstawy pod kątem . Oblicz objętość ostrosłupa.

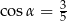Wysokość ostrosłupa prawidłowego czworokątnego jest równa 8. Krawędź boczna jest nachylona do płaszczyzny podstawy pod kątem takim, że cosα = 35 . Oblicz objętość tego ostrosłupa.

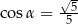Kąt jest kątem nachylenia krawędzi bocznej ostrosłupa prawidłowego czworokątnego do płaszczyzny podstawy (zobacz rysunek). Oblicz stosunek pola powierzchni całkowitej tego ostrosłupa do pola jego podstawy, jeżeli √5- cosα = 5 .

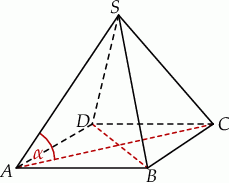
Dany jest ostrosłup prawidłowy czworokątny o wysokości 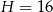H = 16 . Suma długości wszystkich jego krawędzi jest równa 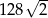√ -- 128 2 . Oblicz cosinus kąta nachylenia ściany bocznej do płaszczyzny podstawy tego ostrosłupa.

Dach wieży ma kształt powierzchni bocznej ostrosłupa prawidłowego czworokątnego, którego krawędź podstawy ma długość 4 m. Ściana boczna tego ostrosłupa jest nachylona do płaszczyzny podstawy pod kątem 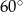60∘ .

Sporządź pomocniczy rysunek i zaznacz na nim podane w zadaniu wielkości.
Oblicz, ile sztuk dachówek należy kupić, aby pokryć ten dach, wiedząc, że do pokrycia 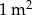potrzebne są 24 dachówki. Przy zakupie należy doliczyć 8% dachówek na zapas.

Krawędź podstawy ostrosłupa prawidłowego czworokątnego 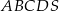ABCDS ma długość . Ściana boczna jest nachylona do płaszczyzny podstawy ostrosłupa pod kątem 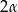. Ostrosłup ten przecięto płaszczyzną, która przechodzi przez krawędź podstawy i dzieli na połowy kąt pomiędzy ścianą boczną i podstawą. Oblicz pole powstałego przekroju tego ostrosłupa.

Oblicz objętość ostrosłupa prawidłowego czworokątnego o krawędzi podstawy 2 dm i krawędzi bocznej 4 dm.

Ukryj Podobne zadania

Oblicz objętość ostrosłupa prawidłowego czworokątnego o krawędzi podstawy 4 dm i krawędzi bocznej 6 dm.

W ostrosłupie prawidłowym czworokątnym 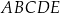ABCDE punkt 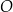jest środkiem symetrii podstawy ostrosłupa. Stosunek obwodu podstawy 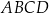ABCD do sumy długości wszystkich krawędzi ostrosłupa jest równy 1:5. Przez przekątną 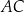podstawy i środek 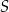krawędzi bocznej 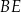poprowadzono płaszczyznę. Oblicz stosunek pola otrzymanego przekroju do pola podstawy ostrosłupa oraz miarę kąta 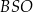BSO (w zaokrągleniu do ).

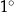Dany jest ostrosłup prawidłowy czworokątny o podstawie 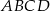ABCD i wierzchołku 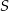. Pole trójkąta 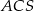ACS jest równe 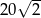√ -- 20 2 , krawędź boczna jest nachylona do płaszczyzny podstawy pod kątem, którego tangens jest równy 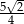5√-2 4 . Oblicz objętość ostrosłupa.

Dany jest ostrosłup prawidłowy czworokątny o krawędzi podstawy 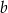i kącie nachylenia krawędzi bocznej do krawędzi podstawy . Oblicz pole przekroju płaszczyzną przechodzącą przez wierzchołek i równoległą do krawędzi podstawy oraz nachyloną do płaszczyzny podstawy pod kątem 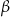. Podaj konieczne założenia dotyczące kąta .

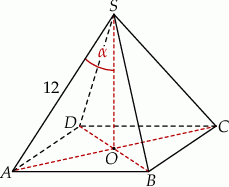
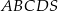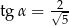Długość krawędzi bocznej ostrosłupa prawidłowego czworokątnego ABCDS jest równa 12 (zobacz rysunek). Krawędź boczna tworzy z wysokością tego ostrosłupa kąt taki, że tg α = 2√-- 5 . Oblicz objętość tego ostrosłupa.

Ukryj Podobne zadania

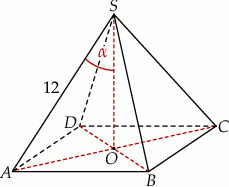
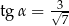Długość krawędzi bocznej ostrosłupa prawidłowego czworokątnego ABCDS jest równa 12 (zobacz rysunek). Krawędź boczna tworzy z wysokością tego ostrosłupa kąt taki, że tg α = 3√-- 7 . Oblicz objętość tego ostrosłupa.

W ostrosłupie prawidłowym czworokątnym o objętości 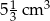1 3 53 cm wysokość jest 2 razy dłuższa od krawędzi podstawy. Oblicz pole powierzchni tego ostrosłupa

W ostrosłupie prawidłowym czworokątnym kąt ostry ściany bocznej przy wierzchołku ostrosłupa ma miarę . Oblicz tangens kąta ostrego 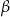, jaki tworzy z płaszczyzną podstawy płaszczyzna przechodząca przez wierzchołek ostrosłupa oraz przez środki dwóch sąsiednich boków podstawy.

Strona 2 z 4