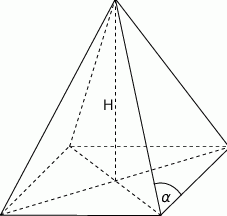
Wszystkie krawędzie ostrosłupa prawidłowego czworokątnego mają tę samą długość. Oblicz kąt nachylenia krawędzi bocznej ostrosłupa do płaszczyzny podstawy.
/Szkoła średnia/Geometria/Stereometria/Ostrosłup/Prawidłowy czworokątny
Krawędź boczna ostrosłupa prawidłowego czworokątnego ma długość 4 cm i jest nachylona do płaszczyzny podstawy pod kątem 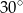 . Oblicz długość krawędzi sześcianu, którego objętość jest równa objętości tego ostrosłupa.
. Oblicz długość krawędzi sześcianu, którego objętość jest równa objętości tego ostrosłupa.
Podstawą ostrosłupa prawidłowego jest kwadrat. Wysokość ściany bocznej tego ostrosłupa jest równa 22, a tangens kąta nachylenia ściany bocznej ostrosłupa do płaszczyzny jego podstawy jest równy 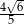 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
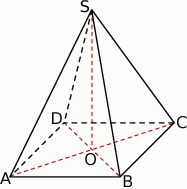
Dany jest sześcian 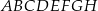 o krawędzi długości 9. Wierzchołki podstawy
o krawędzi długości 9. Wierzchołki podstawy 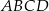 sześcianu połączono odcinkami z punktem
sześcianu połączono odcinkami z punktem 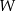 , który jest punktem przecięcia przekątnych podstawy
, który jest punktem przecięcia przekątnych podstawy 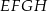 . Otrzymano w ten sposób ostrosłup prawidłowy czworokątny
. Otrzymano w ten sposób ostrosłup prawidłowy czworokątny  .
.
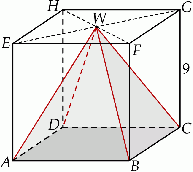
Oblicz cosinus kąta nachylenia krawędzi bocznej ostrosłupa do płaszczyzny podstawy.
Dany jest graniastosłup prawidłowy czworokątny  o krawędzi podstawy równej 9 i wysokości równej 12. Wierzchołki podstawy
o krawędzi podstawy równej 9 i wysokości równej 12. Wierzchołki podstawy  graniastosłupa połączono odcinkami z punktem
graniastosłupa połączono odcinkami z punktem 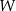 , który jest punktem przecięcia przekątnych podstawy
, który jest punktem przecięcia przekątnych podstawy 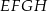 . Otrzymano w ten sposób ostrosłup prawidłowy czworokątny
. Otrzymano w ten sposób ostrosłup prawidłowy czworokątny 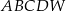 .
.
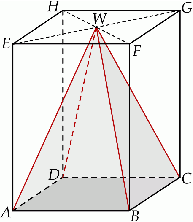
Oblicz cosinus kąta nachylenia krawędzi bocznej ostrosłupa do płaszczyzny podstawy.
Dany jest ostrosłup prawidłowy czworokątny 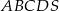 o podstawie
o podstawie 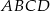 . Ramię trójkąta równoramiennego
. Ramię trójkąta równoramiennego 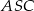 ma długość 8 i jest dwa razy dłuższe od jego podstawy. Oblicz sinus kąta nachylenia ściany bocznej do płaszczyzny podstawy.
ma długość 8 i jest dwa razy dłuższe od jego podstawy. Oblicz sinus kąta nachylenia ściany bocznej do płaszczyzny podstawy.
Objętość ostrosłupa prawidłowego czworokątnego jest równa 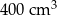 , a jego wysokość jest równa 12 cm. Oblicz pole powierzchni bocznej tego ostrosłupa. Zapisz obliczenia.
, a jego wysokość jest równa 12 cm. Oblicz pole powierzchni bocznej tego ostrosłupa. Zapisz obliczenia.
Krawędź boczna ostrosłupa prawidłowego czworokątnego jest dwa razy dłuższa od krawędzi podstawy. Oblicz cosinus kąta między sąsiednimi ścianami bocznymi.
W ostrosłupie prawidłowym czworokątnym pole podstawy jest dwa razy większe od pola ściany bocznej. Oblicz cosinus kąta między sąsiednimi ścianami bocznymi tego ostrosłupa.
Dany jest ostrosłup prawidłowy czworokątny o objętości 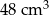 . Ściana boczna jest nachylona do podstawy pod takim kątem
. Ściana boczna jest nachylona do podstawy pod takim kątem  , że
, że 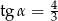 . Wyznacz pole powierzchni bocznej tego ostrosłupa.
. Wyznacz pole powierzchni bocznej tego ostrosłupa.
Krawędź boczna ostrosłupa prawidłowego czworokątnego wpisanego w kulę o promieniu 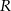 tworzy z płaszczyzną podstawy kąt
tworzy z płaszczyzną podstawy kąt  . Oblicz pole powierzchni całkowitej tego ostrosłupa.
. Oblicz pole powierzchni całkowitej tego ostrosłupa.
Dany jest ostrosłup prawidłowy czworokątny, w którym wszystkie krawędzie mają równą długość. Zaznacz na rysunku kąt utworzony przez dwie sąsiednie ściany boczne tego ostrosłupa i oblicz cosinus tego kąta.
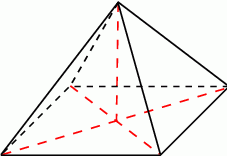
Podstawa ostrosłupa prawidłowego czworokątnego ma pole 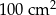 , a jego pole powierzchni bocznej jest równe
, a jego pole powierzchni bocznej jest równe 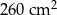 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
Wysokość ostrosłupa prawidłowego czworokątnego tworzy ze ścianą boczną kąt o mierze 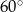 . Pole powierzchni bocznej ostrosłupa jest równe
. Pole powierzchni bocznej ostrosłupa jest równe 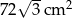 . Oblicz objętość ostrosłupa.
. Oblicz objętość ostrosłupa.
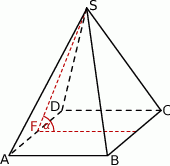
Podstawą ostrosłupa prawidłowego 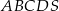 jest kwadrat
jest kwadrat 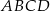 . Punkt
. Punkt 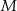 jest środkiem odcinka
jest środkiem odcinka 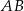 , a punkt
, a punkt 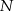 jest środkiem odcinka
jest środkiem odcinka 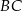 . Trójkąt
. Trójkąt 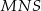 jest równoboczny i jego bok ma długość
jest równoboczny i jego bok ma długość 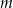 . Oblicz objętość ostrosłupa
. Oblicz objętość ostrosłupa 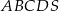 i kąt nachylenia ściany bocznej do płaszczyzny podstawy tego ostrosłupa.
i kąt nachylenia ściany bocznej do płaszczyzny podstawy tego ostrosłupa.
W ostrosłup prawidłowy czworokątny wpisano sześcian tak, że jego cztery wierzchołki należą do krawędzi bocznych ostrosłupa, a pozostałe do płaszczyzny podstawy. Oblicz długość krawędzi sześcianu, jeżeli wysokość ostrosłupa jest równa 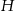 , a długość jego krawędzi podstawy jest równa
, a długość jego krawędzi podstawy jest równa  .
.
Można przyjąć, że piramida Cheopsa jest ostrosłupem prawidłowym czworokątnym o krawędzi podstawy 233 m. Długość cienia piramidy w momencie, gdy promienie słoneczne padają prostopadle do jednej ze ścian wynosi 67,5 m. Wyznacz wysokość piramidy.
Krawędź boczna ostrosłupa prawidłowego czworokątnego ma długość 12 i jest nachylona do płaszczyzny podstawy pod kątem 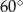 . Oblicz pole powierzchni całkowitej tego ostrosłupa.
. Oblicz pole powierzchni całkowitej tego ostrosłupa.
Wysokość ostrosłupa prawidłowego czworokątnego jest równa 8. Krawędź boczna jest nachylona do płaszczyzny podstawy pod kątem 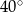 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
Wysokość ostrosłupa prawidłowego czworokątnego jest równa 6. Krawędź boczna jest nachylona do płaszczyzny podstawy pod kątem 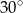 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
Przedstawiona na rysunku bryła to ostrosłup prawidłowy czworokątny ścięty płaszczyzną równoległą do jego płaszczyzny podstawy. Wysokość tej bryły jest równa 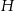 , a
, a  i
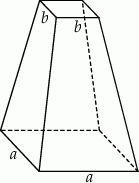
i 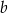 (
(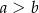 ) są długościami krawędzi jego podstaw. Oblicz objętość tej bryły.
) są długościami krawędzi jego podstaw. Oblicz objętość tej bryły.
Pole przekroju ostrosłupa prawidłowego czworokątnego płaszczyzną przechodzącą przez przekątną podstawy i równoległą do krawędzi bocznej rozłącznej z tą przekątną wynosi  . Oblicz pole przekroju ostrosłupa płaszczyzną zawierającą środki dwóch sąsiednich boków podstawy i środek wysokości ostrosłupa.
. Oblicz pole przekroju ostrosłupa płaszczyzną zawierającą środki dwóch sąsiednich boków podstawy i środek wysokości ostrosłupa.
W ostrosłupie prawidłowym czworokątnym dane są: 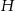 – wysokość ostrosłupa oraz
– wysokość ostrosłupa oraz  — miara kąta utworzonego przez krawędź boczną i krawędź podstawy (
— miara kąta utworzonego przez krawędź boczną i krawędź podstawy (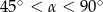 ).
).
- Wykaż, że objętość
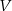 tego ostrosłupa jest równa
tego ostrosłupa jest równa 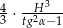 .
. - Oblicz miarę kąta
 , dla której objętość
, dla której objętość 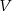 danego ostrosłupa jest równa
danego ostrosłupa jest równa 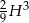 . Wynik podaj w zaookrągleniu do całkowitej liczby stopni.
. Wynik podaj w zaookrągleniu do całkowitej liczby stopni.