Dany jest ostrosłup prawidłowy czworokątny o krawędzi bocznej dwa razy dłuższej od krawędzi podstawy.
-
Wyznacz cosinus kąta nachylenia ściany bocznej do płaszczyzny podstawy ostrosłupa.
-
Wyznacz długość krawędzi ostrosłupa, tak aby pole jego powierzchni bocznej wynosiło
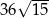 .
.

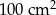 , a jego pole powierzchni bocznej jest równe
, a jego pole powierzchni bocznej jest równe 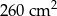 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa. 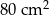 , a pole jego powierzchni całkowitej wynosi
, a pole jego powierzchni całkowitej wynosi 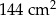 . Oblicz długość krawędzi podstawy i długość krawędzi bocznej tego ostrosłupa. Zapisz obliczenia.
. Oblicz długość krawędzi podstawy i długość krawędzi bocznej tego ostrosłupa. Zapisz obliczenia. 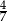 , a pole koła opisanego na podstawie ostrosłupa jest równe
, a pole koła opisanego na podstawie ostrosłupa jest równe 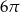 . Oblicz cosinus kąta
. Oblicz cosinus kąta  między sąsiednimi ścianami bocznymi ostrosłupa.
między sąsiednimi ścianami bocznymi ostrosłupa. 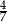 , a pole koła opisanego na podstawie ostrosłupa jest równe
, a pole koła opisanego na podstawie ostrosłupa jest równe 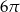 . Oblicz cosinus kąta
. Oblicz cosinus kąta  między sąsiednimi krawędziami bocznymi ostrosłupa.
między sąsiednimi krawędziami bocznymi ostrosłupa. 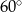 , a krawędź boczna ostrosłupa ma długość
, a krawędź boczna ostrosłupa ma długość 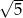 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa. 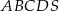 , którego krawędź boczna ma długość 6 (zobacz rysunek). Ściana boczna tego ostrosłupa jest nachylona do płaszczyzny podstawy pod kątem, którego tangens jest równy
, którego krawędź boczna ma długość 6 (zobacz rysunek). Ściana boczna tego ostrosłupa jest nachylona do płaszczyzny podstawy pod kątem, którego tangens jest równy 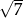 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa. 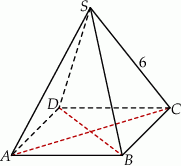
 krawędź boczna ma długość 6, a kąt nachylenia ściany bocznej do płaszczyzny podstawy ostrosłupa ma miarę
krawędź boczna ma długość 6, a kąt nachylenia ściany bocznej do płaszczyzny podstawy ostrosłupa ma miarę 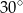 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa. 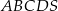 o podstawie
o podstawie 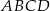 . Krawędź boczna tego ostrosłupa jest o
. Krawędź boczna tego ostrosłupa jest o 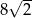 dłuższa od krawędzi podstawy, a wysokość ostrosłupa jest równa 14. Oblicz objętość i pole powierzchni bocznej tego ostrosłupa.
dłuższa od krawędzi podstawy, a wysokość ostrosłupa jest równa 14. Oblicz objętość i pole powierzchni bocznej tego ostrosłupa.  . Dwie sąsiednie ściany boczne ostrosłupa są prostopadłe do płaszczyzny podstawy, a dwie pozostałe ściany boczne tworzą z podstawą kąt
. Dwie sąsiednie ściany boczne ostrosłupa są prostopadłe do płaszczyzny podstawy, a dwie pozostałe ściany boczne tworzą z podstawą kąt  . Oblicz pole powierzchni bocznej ostrosłupa.
. Oblicz pole powierzchni bocznej ostrosłupa. 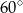 .
.  . Oblicz pole powierzchni całkowitej tego ostrosłupa.
. Oblicz pole powierzchni całkowitej tego ostrosłupa. 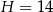 . Cosinus kąta nachylenia krawędzi bocznej do płaszczyzny podstawy tego ostrosłupa jest równy
. Cosinus kąta nachylenia krawędzi bocznej do płaszczyzny podstawy tego ostrosłupa jest równy  . Oblicz pole powierzchni bocznej tego ostrosłupa.
. Oblicz pole powierzchni bocznej tego ostrosłupa. 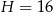 . Cosinus kąta nachylenia krawędzi bocznej do płaszczyzny podstawy tego ostrosłupa jest równy
. Cosinus kąta nachylenia krawędzi bocznej do płaszczyzny podstawy tego ostrosłupa jest równy  . Oblicz pole powierzchni bocznej tego ostrosłupa.
. Oblicz pole powierzchni bocznej tego ostrosłupa.  . Przez wierzchołek ostrosłupa i środki dwóch sąsiednich krawędzi podstawy poprowadzono płaszczyznę . Wyznacz sinus kąta nachylenia wyznaczonego przekroju do podstawy ostrosłupa.
. Przez wierzchołek ostrosłupa i środki dwóch sąsiednich krawędzi podstawy poprowadzono płaszczyznę . Wyznacz sinus kąta nachylenia wyznaczonego przekroju do podstawy ostrosłupa.  , dla którego
, dla którego 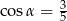 . Wysokość ostrosłupa ma długość 12 cm. Oblicz objętość tego ostrosłupa.
. Wysokość ostrosłupa ma długość 12 cm. Oblicz objętość tego ostrosłupa.  , dla którego
, dla którego 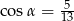 . Wysokość ostrosłupa ma długość 12 cm. Oblicz objętość tego ostrosłupa.
. Wysokość ostrosłupa ma długość 12 cm. Oblicz objętość tego ostrosłupa. 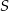 . Kąt płaski przy wierzchołku ostrosłupa ma miarę
. Kąt płaski przy wierzchołku ostrosłupa ma miarę 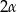 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.  . Wyznacz cosinus kąta między sąsiednimi ścianami bocznymi.
. Wyznacz cosinus kąta między sąsiednimi ścianami bocznymi. 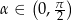 , a krawędź podstawy ma długość
, a krawędź podstawy ma długość  . Przez krawędź podstawy poprowadzono płaszczyznę tworzącą z płaszczyzna podstawy kąt
. Przez krawędź podstawy poprowadzono płaszczyznę tworzącą z płaszczyzna podstawy kąt 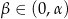 . Wykaż, że pole otrzymanego przekroju jest równe
. Wykaż, że pole otrzymanego przekroju jest równe 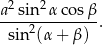
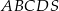 o podstawie
o podstawie 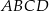 wysokość jest równa
wysokość jest równa 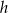 , a kąt między sąsiednimi ścianami bocznymi ostrosłupa ma miarę
, a kąt między sąsiednimi ścianami bocznymi ostrosłupa ma miarę  . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa. 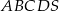 jest równa
jest równa  , a wysokość tego ostrosłupa ma długość
, a wysokość tego ostrosłupa ma długość 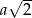 . Punkty
. Punkty 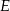 i
i 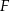 są środkami krawędzi bocznych odpowiednio
są środkami krawędzi bocznych odpowiednio 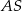 i
i 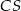 . Oblicz obwód trójkąta
. Oblicz obwód trójkąta 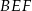 .
.  .
. 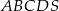 (zobacz rysunek) przekątna
(zobacz rysunek) przekątna 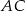 podstawy ma długość
podstawy ma długość 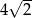 . Kąt
. Kąt 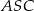 między przeciwległymi krawędziami bocznymi ostrosłupa ma miarę
między przeciwległymi krawędziami bocznymi ostrosłupa ma miarę 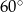 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa. 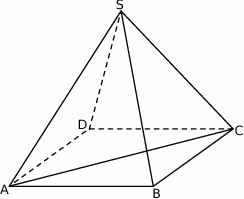
 (zobacz rysunek) przekątna
(zobacz rysunek) przekątna 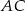 podstawy ma długość 6. Kąt
podstawy ma długość 6. Kąt 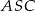 między przeciwległymi krawędziami bocznymi ostrosłupa ma miarę
między przeciwległymi krawędziami bocznymi ostrosłupa ma miarę 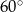 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa. 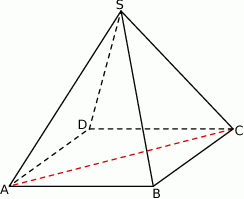
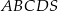 o podstawie
o podstawie 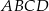 i polu powierzchni bocznej równym
i polu powierzchni bocznej równym 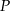 . Kąt między wysokościami sąsiednich ścian bocznych poprowadzonych z wierzchołka
. Kąt między wysokościami sąsiednich ścian bocznych poprowadzonych z wierzchołka 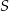 ma miarę
ma miarę 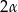 . Objętość tego ostrosłupa jest równa
. Objętość tego ostrosłupa jest równa 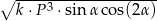 , gdzie
, gdzie 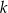 jest stałym współczynnikiem liczbowym. Oblicz współczynnik
jest stałym współczynnikiem liczbowym. Oblicz współczynnik 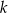 .
.  . Ściana boczna ostrosłupa nachylona jest do płaszczyzny podstawy pod kątem
. Ściana boczna ostrosłupa nachylona jest do płaszczyzny podstawy pod kątem 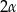 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa. 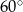 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa. 