Narysuj wykres funkcji 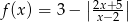 .
.
/Szkoła średnia/Funkcje - wykresy/Wartość bezwzględna/Z wymierną
Na rysunku przedstawiony jest fragment wykresu funkcji określonej wzorem 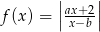 .
.
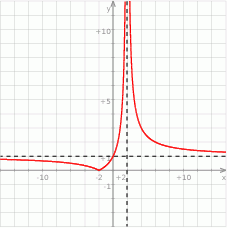
- Oblicz
 i
i 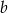 .
. - Narysuj wykres funkcji określonej wzorem
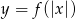 .
. - Podaj wszystkie wartości parametru
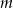 , dla których równanie
, dla których równanie 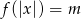 ma cztery rozwiązania.
ma cztery rozwiązania.
Z podanego równania 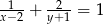 , gdzie
, gdzie 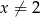 i
i 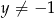 , wyznacz
, wyznacz 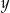 jako funkcję zmiennej
jako funkcję zmiennej  . Narysuj wykres funkcji
. Narysuj wykres funkcji 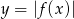 .
.
Dana jest funkcja 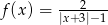 .
.
- Naszkicuj wykres funkcji
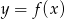 i na jego podstawie wyznacz liczbę rozwiązań równania
i na jego podstawie wyznacz liczbę rozwiązań równania 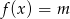 w zależności od parametru
w zależności od parametru 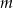 .
. - Liczby
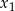 i
i 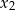 są różnymi pierwiastkami równania
są różnymi pierwiastkami równania 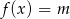 . Oblicz
. Oblicz 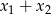 .
.
Napisz wzór i naszkicuj wykres funkcji 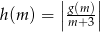 wiedząc, że funkcja
wiedząc, że funkcja 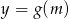 każdej liczbie rzeczywistej
każdej liczbie rzeczywistej 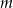 przyporządkowuje najmniejszą wartość funkcji kwadratowej
przyporządkowuje najmniejszą wartość funkcji kwadratowej 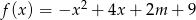 w przedziale
w przedziale 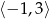 .
.
Prosta 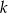 równoległa do osi
równoległa do osi 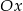 przecina wykres funkcji
przecina wykres funkcji 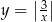 w dwóch punktach
w dwóch punktach 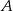 i
i 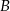 . Wyznacz współrzędne punktów
. Wyznacz współrzędne punktów 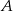 i
i 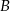 jeżeli wiadomo, że razem z punktem
jeżeli wiadomo, że razem z punktem 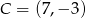 tworzą trójkąt o polu 12.
tworzą trójkąt o polu 12.
Prosta 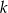 równoległa do osi
równoległa do osi 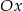 przecina wykres funkcji
przecina wykres funkcji 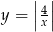 w dwóch punktach
w dwóch punktach 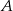 i
i 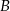 . Wyznacz współrzędne punktów
. Wyznacz współrzędne punktów 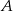 i
i 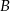 jeżeli wiadomo, że razem z punktem
jeżeli wiadomo, że razem z punktem 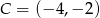 tworzą trójkąt o polu 6.
tworzą trójkąt o polu 6.
Proste 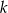 i
i 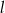 są równoległe do osi
są równoległe do osi 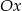 i przecinają wykres funkcji
i przecinają wykres funkcji 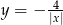 odpowiednio w punktach
odpowiednio w punktach 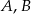 i
i 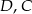 w ten sposób, że czworokąt
w ten sposób, że czworokąt 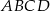 jest trapezem o polu 6 i wysokości 2. Oblicz obwód trapezu
jest trapezem o polu 6 i wysokości 2. Oblicz obwód trapezu 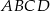 .
.
Narysuj wykres funkcji 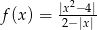 , a następnie określ, dla jakich wartości parametru
, a następnie określ, dla jakich wartości parametru 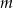 równanie
równanie 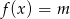 nie ma rozwiązania.
nie ma rozwiązania.

