Niech 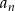 , dla
, dla 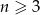 będzie liczbą krawędzi graniastosłupa prostego o podstawie będącej
będzie liczbą krawędzi graniastosłupa prostego o podstawie będącej  -kątem foremnym.
-kątem foremnym.
- Wyznacz wzór ciągu
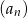 .
. - Sprawdź czy ciąg
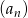 jest ciągiem arytmetycznym.
jest ciągiem arytmetycznym. - Uzasadnij, że żaden wyraz tego ciągu nie jest równy 2009.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Niech 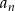 , dla
, dla 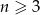 będzie liczbą krawędzi graniastosłupa prostego o podstawie będącej
będzie liczbą krawędzi graniastosłupa prostego o podstawie będącej  -kątem foremnym.
-kątem foremnym.
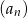 .
. 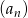 jest ciągiem arytmetycznym.
jest ciągiem arytmetycznym. Długości boków trójkąta prostokątnego tworzą ciąg arytmetyczny. Jedna z przyprostokątnych ma długość 6. Jaką długość ma druga przyprostokątna oraz przeciwprostokątna?
Ciąg 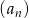 jest określony wzorem
jest określony wzorem 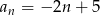 . Uzasadnij (na podstawie definicji) że ciąg
. Uzasadnij (na podstawie definicji) że ciąg 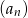 jest arytmetyczny.
jest arytmetyczny.
Wykaż, że ciąg liczbowy o wyrazie ogólnym 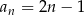 , gdzie
, gdzie 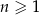 , jest ciągiem arytmetycznym.
, jest ciągiem arytmetycznym.
Wykaż, że ciąg o wzorze ogólnym 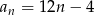 , gdzie
, gdzie 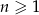 , jest ciągiem arytmetycznym.
, jest ciągiem arytmetycznym.
Wykaż, że ciąg liczbowy o wyrazie ogólnym 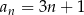 , gdzie
, gdzie 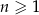 , jest ciągiem arytmetycznym.
, jest ciągiem arytmetycznym.
Dany jest ciąg 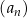 określony wzorem ogólnym
określony wzorem ogólnym 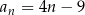 dla każdej liczby naturalnej
dla każdej liczby naturalnej 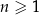 . Wykaż, że ciąg
. Wykaż, że ciąg 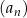 jest arytmetyczny.
jest arytmetyczny.
Wykaż, że ciąg o wzorze ogólnym 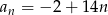 , gdzie
, gdzie 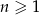 , jest ciągiem arytmetycznym.
, jest ciągiem arytmetycznym.
W ciągu arytmetycznym suma pierwszego i trzeciego wyrazu jest równa 2, a iloraz pierwszego i czwartego jest równy 1.
 początkowych wyrazów tego ciągu.
początkowych wyrazów tego ciągu.  , dla których suma
, dla których suma  kolejnych, początkowych wyrazów ciągu jest mniejsza od 50.
kolejnych, początkowych wyrazów ciągu jest mniejsza od 50.W trójkącie prostokątnym jedna z przyprostokątnych jest średnią arytmetyczną drugiej przyprostokątnej i przeciwprostokątnej. Oblicz sinusy kątów ostrych tego trójkąta.
W trójkącie prostokątnym stosunek różnicy długości przyprostokątnych do długości przeciwprostokątnej jest równy 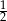 . Oblicz cosinusy kątów ostrych tego trójkąta.
. Oblicz cosinusy kątów ostrych tego trójkąta.
W trójkącie prostokątnym stosunek sumy długości przyprostokątnych do długości przeciwprostokątnej jest równy  . Oblicz cosinusy kątów ostrych tego trójkąta.
. Oblicz cosinusy kątów ostrych tego trójkąta.
Trzy początkowe wyrazy malejącego ciągu arytmetycznego są pierwiastkami wielomianu 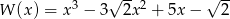 , a jednym z nich jest
, a jednym z nich jest 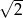 .
.
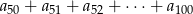 .
.Dla jakich wartości parametru 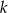 równanie
równanie 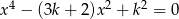 ma co najmniej trzy różne pierwiastki, które są kolejnymi wyrazami ciągu arytmetycznego?
ma co najmniej trzy różne pierwiastki, które są kolejnymi wyrazami ciągu arytmetycznego?
Ciąg 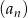 jest arytmetyczny oraz
jest arytmetyczny oraz 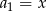 i
i 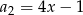 . Wiedząc, że
. Wiedząc, że 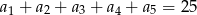 oblicz
oblicz  oraz sumę
oraz sumę 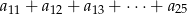 .
.
Liczby 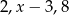 są w podanej kolejności pierwszym, drugim i czwartym wyrazem ciągu arytmetycznego. Oblicz
są w podanej kolejności pierwszym, drugim i czwartym wyrazem ciągu arytmetycznego. Oblicz  .
.
Liczby 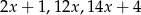 są w podanej kolejności pierwszym, drugim i czwartym wyrazem ciągu arytmetycznego. Oblicz
są w podanej kolejności pierwszym, drugim i czwartym wyrazem ciągu arytmetycznego. Oblicz  .
.
Obwód trapezu równoramiennego wynosi 116. Oblicz pole tego trapezu, jeśli długości ramienia i podstaw trapezu są (w podanej kolejności) trzema kolejnymi wyrazami ciągu arytmetycznego oraz długość odcinka łączącego środki ramion trapezu wynosi 41.
Ciąg arytmetyczny 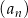 jest określony dla każdej liczby naturalnej
jest określony dla każdej liczby naturalnej 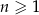 . Różnicą tego ciągu jest liczba
. Różnicą tego ciągu jest liczba 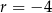 , a średnia arytmetyczna początkowych sześciu wyrazów tego ciągu:
, a średnia arytmetyczna początkowych sześciu wyrazów tego ciągu: 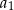 ,
, 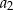 ,
, 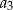 ,
, 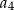 ,
, 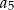 ,
, 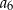 , jest równa 16.
, jest równa 16.
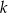 , dla której
, dla której 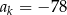 .
.Ciąg arytmetyczny 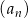 jest określony dla każdej liczby naturalnej
jest określony dla każdej liczby naturalnej 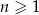 . Różnicą tego ciągu jest liczba
. Różnicą tego ciągu jest liczba 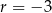 , a średnia arytmetyczna początkowych siedmiu wyrazów tego ciągu:
, a średnia arytmetyczna początkowych siedmiu wyrazów tego ciągu: 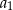 ,
, 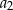 ,
, 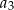 ,
, 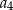 ,
, 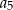 ,
, 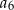 ,
, 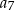 , jest równa
, jest równa 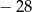 .
.
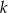 , dla której
, dla której 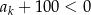 .
.Dany jest ciąg arytmetyczny 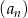 określony dla każdej liczby naturalnej
określony dla każdej liczby naturalnej 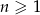 , w którym suma pierwszych 50 wyrazów jest równa 9 900, a suma wyrazów o numerach od 41 do 70 (włącznie) jest równa 540. Oblicz sumę wszystkich dodatnich wyrazów tego ciągu.
, w którym suma pierwszych 50 wyrazów jest równa 9 900, a suma wyrazów o numerach od 41 do 70 (włącznie) jest równa 540. Oblicz sumę wszystkich dodatnich wyrazów tego ciągu.
Dany jest ciąg arytmetyczny 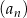 określony dla każdej liczby naturalnej
określony dla każdej liczby naturalnej 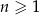 , w którym suma pierwszych 60 wyrazów jest równa 108 750, a suma wyrazów o numerach od 31 do 50 (włącznie) jest równa 34 850. Wyznacz największy wyraz tego ciągu.
, w którym suma pierwszych 60 wyrazów jest równa 108 750, a suma wyrazów o numerach od 31 do 50 (włącznie) jest równa 34 850. Wyznacz największy wyraz tego ciągu.
W siedmiowyrazowym ciągu arytmetycznym środkowy wyraz jest równy 0. Udowodnij, że suma wyrazów tego ciągu jest równa 0.
Dany jest ciąg 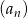 , w którym suma
, w którym suma  początkowych wyrazów wyraża się wzorem
początkowych wyrazów wyraża się wzorem 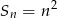 ,
, 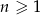 . Wyznacz wzór ogólny ciągu. Czy jest to ciąg arytmetyczny?
. Wyznacz wzór ogólny ciągu. Czy jest to ciąg arytmetyczny?
Dany jest ciąg 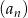 , w którym suma
, w którym suma  początkowych wyrazów wyraża się wzorem
początkowych wyrazów wyraża się wzorem 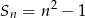 ,
, 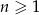 . Wyznacz wzór ogólny ciągu. Czy jest to ciąg arytmetyczny?
. Wyznacz wzór ogólny ciągu. Czy jest to ciąg arytmetyczny?
Dany jest skończony ciąg, w którym pierwszy wyraz jest równy 444, a ostatni jest równy 653. Każdy wyraz tego ciągu, począwszy od drugiego, jest o 11 większy od wyrazu bezpośrednio go poprzedzającego. Oblicz sumę wszystkich wyrazów tego ciągu.
Długości boków trójkąta prostokątnego o obwodzie 30 cm są pierwszym, piętnastym i siedemnastym wyrazem rosnącego ciągu arytmetycznego. Oblicz pole tego trójkąta.
Trójwyrazowy ciąg 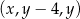 jest arytmetyczny. Suma wszystkich wyrazów tego ciągu jest równa 6. Oblicz wszystkie wyrazy tego ciągu.
jest arytmetyczny. Suma wszystkich wyrazów tego ciągu jest równa 6. Oblicz wszystkie wyrazy tego ciągu.
W skończonym ciągu arytmetycznym 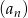 pierwszy wyraz
pierwszy wyraz 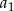 jest równy 7 oraz ostatni wyraz
jest równy 7 oraz ostatni wyraz 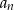 jest równy 89. Suma wszystkich wyrazów tego ciągu jest równa 2016. Oblicz, ile wyrazów ma ten ciąg.
jest równy 89. Suma wszystkich wyrazów tego ciągu jest równa 2016. Oblicz, ile wyrazów ma ten ciąg.
W skończonym ciągu arytmetycznym 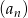 pierwszy wyraz
pierwszy wyraz 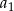 jest równy 9 oraz ostatni wyraz
jest równy 9 oraz ostatni wyraz 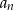 jest równy 93. Suma wszystkich wyrazów tego ciągu jest równa 2295. Oblicz, ile wyrazów ma ten ciąg.
jest równy 93. Suma wszystkich wyrazów tego ciągu jest równa 2295. Oblicz, ile wyrazów ma ten ciąg.
Liczby 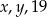 w podanej kolejności tworzą ciąg arytmetyczny, przy czym
w podanej kolejności tworzą ciąg arytmetyczny, przy czym 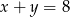 . Oblicz
. Oblicz  i
i 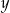 .
.
Liczby 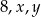 w podanej kolejności tworzą ciąg arytmetyczny, przy czym
w podanej kolejności tworzą ciąg arytmetyczny, przy czym 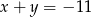 . Oblicz
. Oblicz  i
i 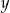 .
.
Znajdź ogólny wyraz ciągu arytmetycznego 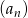 wiedząc, że
wiedząc, że 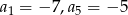 .
.
