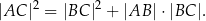Każdy kąt trójkąta  ma miarę mniejszą niż
ma miarę mniejszą niż  . Na bokach tego trójkąta zbudowano trójkąty równoboczne
. Na bokach tego trójkąta zbudowano trójkąty równoboczne  ,
, 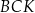 i
i 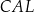 (zobacz rysunek).
(zobacz rysunek).
-
Wykaż, że
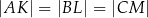 .
. -
Wykaż, że proste
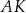 ,
, 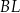 i
i 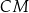 przecinają się w jednym punkcie (jest to tzw. punkt Torricellego-Fermata).
przecinają się w jednym punkcie (jest to tzw. punkt Torricellego-Fermata).
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
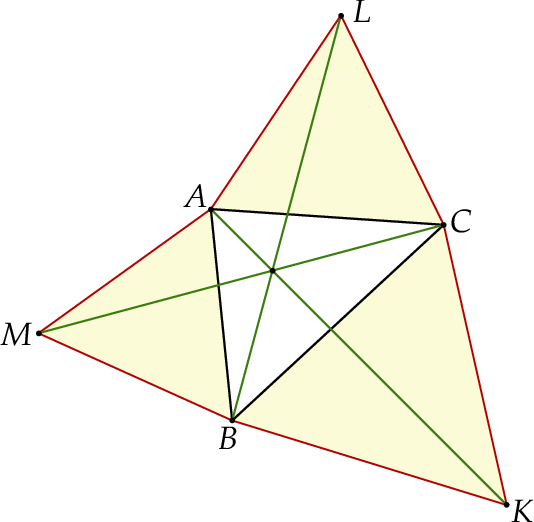
Każdy kąt trójkąta 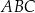 ma miarę mniejszą niż
ma miarę mniejszą niż 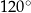 . Na bokach tego trójkąta zbudowano trójkąty równoboczne
. Na bokach tego trójkąta zbudowano trójkąty równoboczne 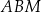 ,
, 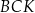 i
i 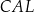 (zobacz rysunek).
(zobacz rysunek).

Wykaż, że 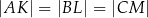 .
.
Wykaż, że proste 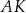 ,
, 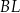 i
i 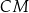 przecinają się w jednym punkcie (jest to tzw. punkt Torricellego-Fermata).
przecinają się w jednym punkcie (jest to tzw. punkt Torricellego-Fermata).
Punkt 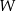 jest środkiem okręgu wpisanego w trójkąt
jest środkiem okręgu wpisanego w trójkąt 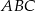 . Prosta przechodząca przez punkty
. Prosta przechodząca przez punkty 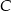 i
i 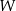 przecina okrąg opisany na trójkącie
przecina okrąg opisany na trójkącie 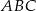 w punkcie
w punkcie 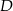 . Wykaż, że trójkąt
. Wykaż, że trójkąt 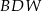 jest równoramienny.
jest równoramienny.
Obwód trójkąta 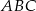 jest równy 8. Oblicz obwód trójkąta
jest równy 8. Oblicz obwód trójkąta 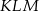 o wierzchołkach będących środkami środkowych trójkąta
o wierzchołkach będących środkami środkowych trójkąta 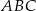 .
.
Dany jest trójkąt 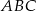 , w którym
, w którym 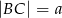 . Z wierzchołka
. Z wierzchołka 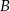 poprowadzono środkową
poprowadzono środkową 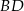 do boku
do boku 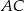 . Punkt
. Punkt 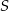 jest środkiem odcinka
jest środkiem odcinka 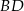 . Przez punkty
. Przez punkty 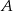 i
i 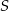 poprowadzono prostą, która przecięła bok
poprowadzono prostą, która przecięła bok 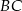 w punkcie
w punkcie 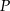 . Wykaż, że długość odcinka
. Wykaż, że długość odcinka 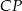 jest równa
jest równa 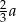 .
.
Dany jest trójkąt 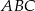 oraz punkt
oraz punkt  na jego boku
na jego boku 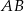 taki, że
taki, że 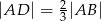 . Z wierzchołka
. Z wierzchołka  poprowadzono środkową
poprowadzono środkową 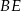 do boku
do boku 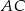 . Punkt
. Punkt 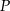 jest punktem wspólnym odcinków
jest punktem wspólnym odcinków 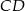 i
i 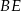 . Wykaż, że punkt
. Wykaż, że punkt 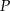 jest środkiem odcinka
jest środkiem odcinka 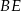 .
.
W trójkącie 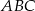 na boku
na boku 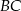 zaznaczono punkt
zaznaczono punkt 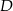 , na boku
, na boku 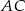 zaznaczono punkt
zaznaczono punkt 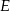 , na boku
, na boku 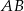 punkt
punkt 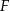 . Poprowadzono okręgi
. Poprowadzono okręgi 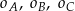 , w ten sposób, że do okręgu
, w ten sposób, że do okręgu 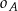 należą punkty
należą punkty 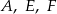 , do
, do 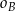 – punkty
– punkty 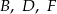 , a do
, a do 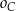 – punkty
– punkty 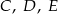 . Wykaż, że te trzy okręgi przecinają się w jednym punkcie.
. Wykaż, że te trzy okręgi przecinają się w jednym punkcie.
Okrąg 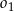 przechodzi przez wierzchołek
przechodzi przez wierzchołek 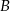 trójkąta
trójkąta 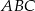 i przecina jego boki
i przecina jego boki 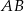 i
i 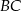 odpowiednio w punktach
odpowiednio w punktach 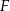 i
i 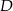 . Okrąg
. Okrąg 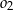 przechodzi przez wierzchołek
przechodzi przez wierzchołek 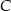 , przecina okrąg
, przecina okrąg 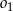 w punkcie
w punkcie 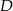 oraz w punkcie
oraz w punkcie 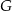 leżącym wewnątrz trójkąta
leżącym wewnątrz trójkąta 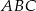 . Ponadto okrąg
. Ponadto okrąg 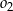 przecina bok
przecina bok 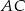 trójkąta w punkcie
trójkąta w punkcie 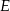 .
.
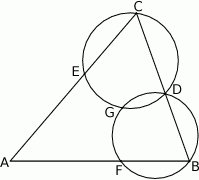
Udowodnij, że punkt 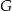 leży na okręgu opisanym na trójkącie
leży na okręgu opisanym na trójkącie 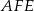 .
.
Każdy kąt trójkąta 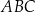 ma miarę mniejszą od
ma miarę mniejszą od 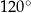 . Wyznacz taki punkt
. Wyznacz taki punkt 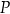 wewnątrz trójkąta
wewnątrz trójkąta 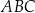 , dla którego suma
, dla którego suma 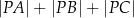 jest najmniejsza możliwa.
jest najmniejsza możliwa.
Wewnątrz trójąta  obrano punkt
obrano punkt  odległy od prostych
odległy od prostych 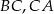 i
i 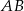 odpowiednio o
odpowiednio o 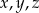 . Wykaż że
. Wykaż że
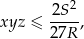
gdzie 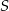 jest polem trójkąta, a
jest polem trójkąta, a 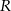 promieniem okręgu opisanego. Dla jakich punktów
promieniem okręgu opisanego. Dla jakich punktów 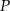 zachodzi równość?
zachodzi równość?
Odcinek 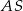 jest środkową trójkąta
jest środkową trójkąta 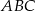 . Udowodnij, że
. Udowodnij, że 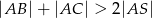 .
.
Wykaż, że suma odległości dowolnego punktu wewnętrznego trójkąta od jego wierzchołków jest większa od połowy obwodu trójkąta.
Każdy kąt trójkąta 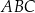 ma miarę mniejszą niż
ma miarę mniejszą niż 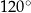 . Udowodnij, że wewnątrz trójkąta
. Udowodnij, że wewnątrz trójkąta 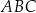 istnieje punkt
istnieje punkt 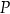 taki, że
taki, że
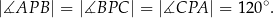
W trójkącie 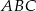 , o bokach długości
, o bokach długości 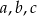 , połączono odcinkiem wierzchołek
, połączono odcinkiem wierzchołek 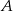 z punktem
z punktem 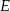 na boku
na boku 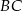 takim, że
takim, że 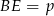 i
i 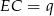 . Uzasadnij, że jeżeli
. Uzasadnij, że jeżeli 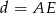 , to
, to 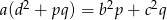 (twierdzenie Stewarta).
(twierdzenie Stewarta).
Oblicz jaka może być najmniejsza możliwa długość boku 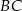 trójkąta
trójkąta  jeżeli
jeżeli  i pole trójkąta
i pole trójkąta  jest równe
jest równe 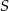 .
.
W trójkącie 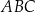 kąt
kąt 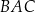 jest dwa razy większy od kąta
jest dwa razy większy od kąta 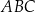 . Wykaż, że prawdziwa jest równość
. Wykaż, że prawdziwa jest równość 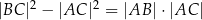 .
.
Dany jest trójkąt 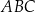 , który nie jest równoramienny. W tym trójkącie miara kąta
, który nie jest równoramienny. W tym trójkącie miara kąta 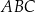 jest dwa razy większa od miary kąta
jest dwa razy większa od miary kąta 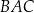 . Wykaż, że długości boków tego trójkąta spełniają warunek
. Wykaż, że długości boków tego trójkąta spełniają warunek