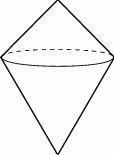
Boja ma kształt dwóch stożków połączonych podstawami, przy czym kąty rozwarcia tych stożków są równe 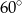 i
i 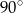 , a odległość ich wierzchołków jest równa
, a odległość ich wierzchołków jest równa 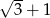 . Oblicz pole powierzchni tej boi.
. Oblicz pole powierzchni tej boi.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Boja ma kształt dwóch stożków połączonych podstawami, przy czym kąty rozwarcia tych stożków są równe 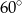 i
i 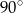 , a odległość ich wierzchołków jest równa
, a odległość ich wierzchołków jest równa 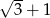 . Oblicz pole powierzchni tej boi.
. Oblicz pole powierzchni tej boi.

Dwie szkoły mają prostokątne boiska. Przekątna każdego boiska jest równa 65 m. Boisko w drugiej szkole ma długość o 4 m większą niż boisko w pierwszej szkole, ale szerokość o 8 m mniejszą. Oblicz długość i szerokość każdego z tych boisk.
Z dwóch okrągłych kawałków blachy o średnicy 25 cm wycięto dwa prostokąty w ten sposób, że wierzchołki prostokątów znajdowały się na brzegu kół (patrz rysunek).
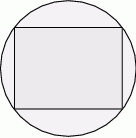
Pierwszy prostokąt miał długość o 4 cm większą niż drugi prostokąt, ale szerokość o 8 cm mniejszą. Oblicz długość i szerokość każdego z prostokątów.
Do wyznaczenia trzech boków pewnego kąpieliska w kształcie prostokąta należy użyć liny o długości 200 m. Czwarty bok tego kąpieliska będzie pokrywał się z brzegiem plaży, który w tym miejscu jest linią prostą (zobacz rysunek).
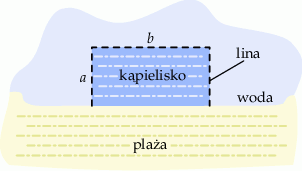
Oblicz wymiary  i
i 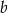 kąpieliska tak, aby jego powierzchnia była największa.
kąpieliska tak, aby jego powierzchnia była największa.
Powierzchnia magazynowa będzie się składała z dwóch identycznych prostokątnych działek połączonych wspólnym bokiem. Całość ma być ogrodzona płotem, przy czym obie działki będzie rozdzielał wspólny płot. W ogrodzeniu będą zamontowane dwie bramy wjazdowe, każda o szerokości 10 m (zobacz rysunek poniżej). Łączna długość płotu ogradzającego oraz rozdzielającego obie działki wyniesie 580 metrów, przy czym szerokości obu bram wjazdowych nie wliczają się w długość płotu.
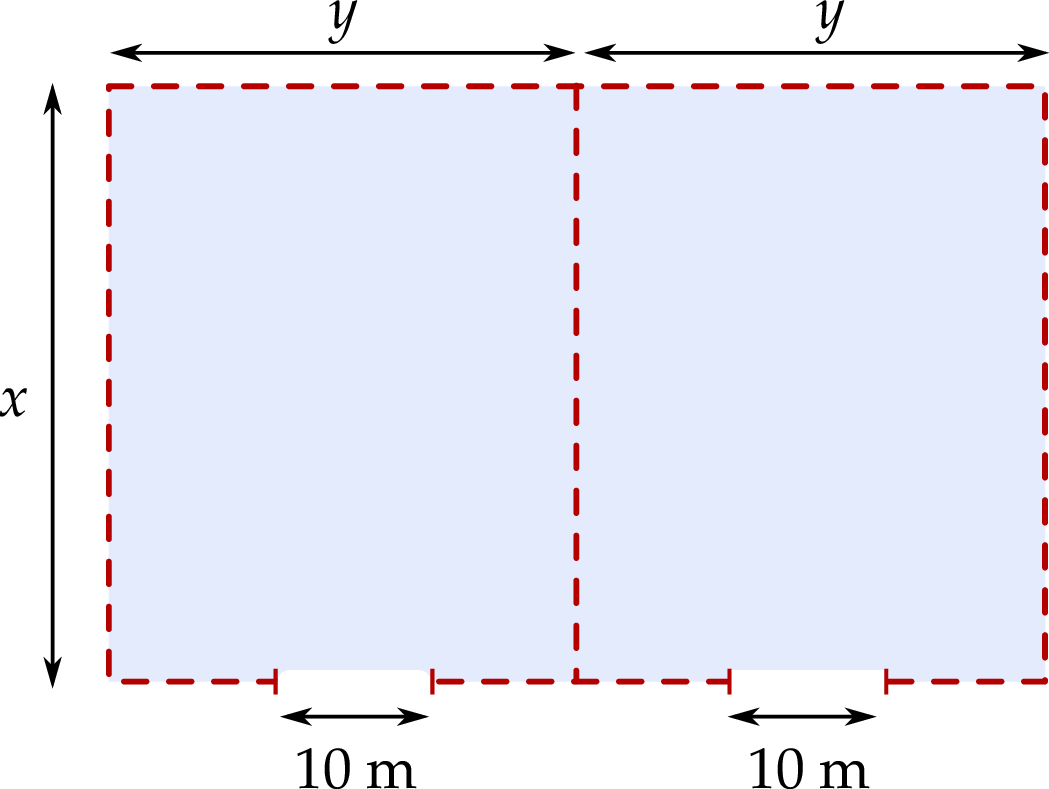
Oblicz wymiary  oraz
oraz 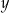 każdej z dwóch prostokątnych działek, tak aby całkowite pole powierzchni magazynowej było największe.
każdej z dwóch prostokątnych działek, tak aby całkowite pole powierzchni magazynowej było największe.
W schronisku dla zwierząt, na płaskiej powierzchni, należy zbudować ogrodzenie z siatki wydzielające trzy identyczne wybiegi o wspólnych ścianach wewnętrznych. Podstawą każdego z tych trzech wybiegów jest prostokąt (jak pokazano na rysunku). Do wykonania tego ogrodzenia należy zużyć 36 metrów bieżących siatki.
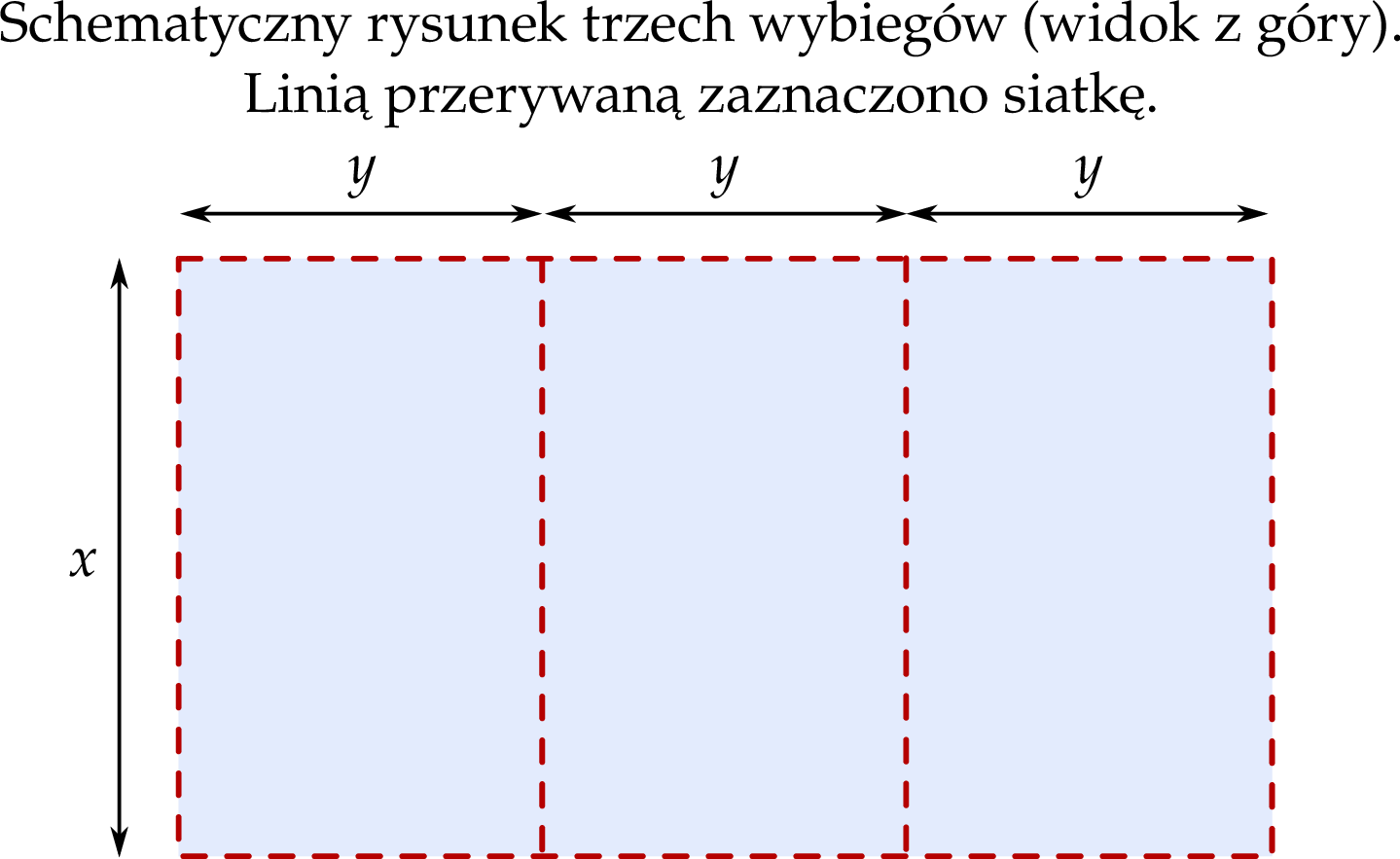
Oblicz wymiary  oraz
oraz 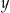 jednego wybiegu, przy których suma pól podstaw tych trzech wybiegów będzie największa. W obliczeniach pomiń szerokość wejścia na każdy z wybiegów.
jednego wybiegu, przy których suma pól podstaw tych trzech wybiegów będzie największa. W obliczeniach pomiń szerokość wejścia na każdy z wybiegów.
Do wyznaczenia boków pewnego kąpieliska w kształcie prostokąta należy użyć liny o długości 80 m. Część jednego z boków tego kąpieliska będzie pokrywać się z końcem pomostu i na tym odcinku lina nie jest potrzebna (zobacz rysunek). Pomost ma szerokość 4 metrów.
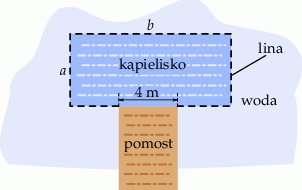
Oblicz wymiary  i
i 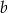 kąpieliska tak, aby jego powierzchnia była największa.
kąpieliska tak, aby jego powierzchnia była największa.
Do wyznaczenia trzech pastwisk na pewnej łące należy użyć ogrodzenia elektrycznego o łącznej długości 960 metrów. Dwa z tych pastwisk mają mieć kwadratowy kształt, a trzecie ma mieć kształt prostokąta, którego jeden z boków jest dwa razy dłuższy od boku pastwiska w kształcie kwadratu (zobacz rysunek).
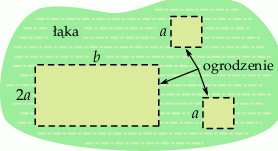
Oblicz wymiary  i
i 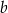 tych pastwisk tak, aby ich łączna powierzchnia była największa możliwa. Oblicz tą największą powierzchnię.
tych pastwisk tak, aby ich łączna powierzchnia była największa możliwa. Oblicz tą największą powierzchnię.
Kostki pozbruku mają kształt graniastosłupów prawidłowych sześciokątnych.
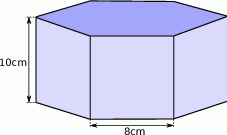
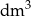 ) zużyto do wyprodukowania 100 takich kostek? Wyniki podaj z dokładnością do 0,01.
) zużyto do wyprodukowania 100 takich kostek? Wyniki podaj z dokładnością do 0,01.Trawnik ma kształt trójkąta równoramiennego o podstawie 80 m i ramionach długości 50 m. Z powierzchni trawnika postanowiono wydzielić prostokątny plac zabaw w ten sposób, że dwa z wierzchołków tego prostokąta leżą na podstawie, a pozostałe dwa na ramionach trójkąta ograniczającego trawnik (zobacz rysunek).
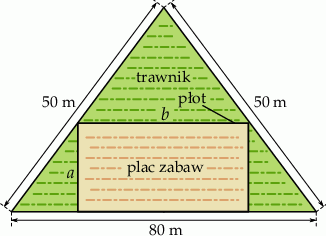
Oblicz wymiary  i
i 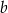 placu zabaw, tak, aby jego pole było największe możliwe.
placu zabaw, tak, aby jego pole było największe możliwe.
Działkę w kształcie trapezu podzielono przekątnymi na 4 działki. Spośród tych czterech działek wskaż dwie o równych polach. Odpowiedź uzasadnij.
Koparka, pogłębiająca rów melioracyjny, usypała kopiec w kształcie stożka. Tworząca tego stożka jest nachylona do płaszczyzny podstawy pod kątem, którego tangens jest równy 1,5. Przyjmując 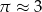 , obliczono, że obwód podstawy kopca jest równy około 12 m. Oblicz, ile kursów będzie musiała wykonać ciężarówka, aby wywieźć wykopany piasek, jeżeli jednorazowo może zabrać
, obliczono, że obwód podstawy kopca jest równy około 12 m. Oblicz, ile kursów będzie musiała wykonać ciężarówka, aby wywieźć wykopany piasek, jeżeli jednorazowo może zabrać 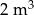 piasku. Przyjmij również, że
piasku. Przyjmij również, że 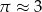 .
.
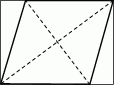
Paweł zamówił szybę w kształcie rombu o przekątnych 40 cm i 30 cm. Zaproponował szklarzowi, by wyciął romb z prostokątnego kawałka szyby, tak jak na rysunku. Jakie wymiary ma ten prostokątny kawałek szyby?
Przed wejściem do przychodni lekarskiej znajdują się schody mające 8 stopni po 15 cm wysokości każdy. Obok schodów jest podjazd dla niepełnosprawnych o nachyleniu 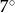 . Oblicz długość podjazdu. Wynik podaj w zaokrągleniu do 10 cm. (
. Oblicz długość podjazdu. Wynik podaj w zaokrągleniu do 10 cm. (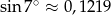 )
)
Ewa jadąc drogą widziała elektrownię wiatrową oznaczoną na rysunku literą 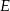 . Z punktu
. Z punktu 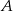 widziała ją pod kątem
widziała ją pod kątem 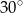 stopni do kierunku drogi. A z punktu
stopni do kierunku drogi. A z punktu 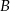 pod kątem
pod kątem 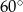 . Przejeżdżając przez punkt
. Przejeżdżając przez punkt 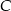 minęła elektrownię. Długość odcinka
minęła elektrownię. Długość odcinka 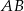 jest równa 20km.
jest równa 20km.
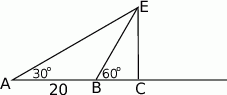
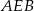 i
i 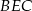 .
. 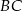 .
. W rachunkach przyjmij, że 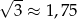 .
.
Dziesięć kul bilardowych średnicy 6 cm umieszczono w prostokątnym pudełku tak jako pokazano to na rysunku.
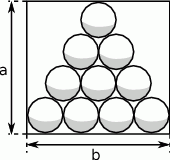
Wyznacz wymiary  i
i 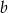 tego pudełka.
tego pudełka.
Huta szkła produkuje kulki szklane o promieniu 5 cm. Do wysyłki będą one pakowane po 4 sztuki w sztywne pudełka w kształcie walca, którego wysokość wynosi 10 cm, a średnica 24 cm. Czy dobrze została dobrana średnica tych pudełek?
Czy kwadratowe lustro o boku długości 2,2 m można przenieść przez drzwi o szerokości 1 m i wysokości 2 m?
Obserwator stojący na płaskiej, poziomej powierzchni widzi pionową wieżę pod kątem 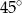 , a po zbliżeniu się do niej o 20m pod kątem
, a po zbliżeniu się do niej o 20m pod kątem 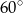 . Oblicz wysokość wieży, wynik zaokrąglij do 1cm.
. Oblicz wysokość wieży, wynik zaokrąglij do 1cm.
Z kawałka materiału w kształcie czworokąta wypukłego o obwodzie 8m wycięto koło o polu 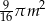 styczne do wszystkich boków czworokąta. Oblicz pole figury powstałej z tego czworokąta po wycięciu koła, z dokładnością do
styczne do wszystkich boków czworokąta. Oblicz pole figury powstałej z tego czworokąta po wycięciu koła, z dokładnością do 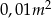 .
.
Rysunek przedstawia kształt obszaru zakreślanego przez wycieraczkę samochodową.
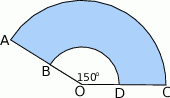
Wiedząc, że 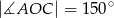 oraz
oraz 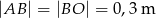 oblicz jakie jest pole obszaru oczyszczanego przez wycieraczkę. Przyjmując, że
oblicz jakie jest pole obszaru oczyszczanego przez wycieraczkę. Przyjmując, że 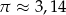 podaj wynik z dokładnością do
podaj wynik z dokładnością do 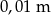 .
.
Oblicz szerokość prostokątnej ramy obrazu wiedząc, że obwód zewnętrzny ramy jest o 28 cm większy od obwodu wewnętrznego tej ramy.
Kule o jednakowych promieniach ułożono w rzędach tworząc w ten sposób kwadrat. Gdyby usunięto 669 kul, to z pozostałych można by było zbudować trójkąt równoboczny (w pierwszym rzędzie jedna kula, w drugim dwie, w trzecim trzy itd.) Bok trójkąta równobocznego zawierałby wówczas o 8 kul więcej niż bok kwadratu. Z ilu kul zbudowany był kwadrat?
