Geometryczne/Zadania z treścią - zadania z matematyki

/Szkoła średnia/Zadania z treścią/Geometryczne

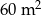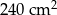Pole powierzchni mieszkania jest równe 2 60 m . Janek sporządził plan tego mieszkania. Jaką skalę zastosował Janek, jeśli pole powierzchni planu mieszkania było równe 24 0 cm 2 .

Ukryj Podobne zadania

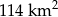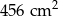Wyznacz skalę mapy, na której jezioro o rzeczywistej powierzchni 2 114 km , zajmuje obszar 456 cm 2 .

Pole każdej z dwóch prostokątnych działek jest równe 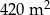2 4 20 m . Szerokość pierwszej działki jest o 8 m większa od szerokości drugiej, ale jej długość jest o 14 m mniejsza. Oblicz szerokość i długość każdej z działek.

Ukryj Podobne zadania

Pole każdej z dwóch prostokątnych działek jest równe 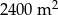2 2 400 m . Szerokość pierwszej działki jest o 8 m większa od szerokości drugiej, ale jej długość jest o 10 m mniejsza. Oblicz szerokość i długość każdej z działek.

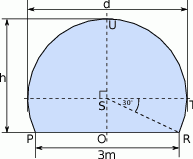
W architekturze islamu często stosowanym elementem był łuk podkowiasty. Schemat okna w kształcie takiego łuku (łuku okręgu) przedstawiono na rysunku poniżej. Korzystając z danych na rysunku oblicz wysokość okna 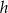i największy prześwit .

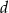Przekrój betonowego kanału melioracyjnego ma kształt trapezu o podstawach 0,5 m i 1,5 m.

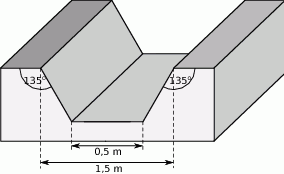
Oblicz ile wody zmieści się w takim kanale, jeżeli jego długość jest równa 50 m.

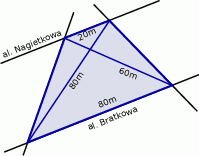
Działka budowlana Andrzeja ograniczona jest dwiema równoległymi alejami i dwoma innymi lokalnymi drogami. Andrzej zmierzył odcinki alei ograniczające działki (80 m i 20 m) oraz długości dwóch ścieżek znajdujących się na terenie tej działki, łączących jej przeciwległe rogi (80 m i 60 m). Następnie wykonał plan tej działki w skali 1:200 i wyznaczył pole powierzchni planu działki. Ile ono wynosiło?

Drzewo rzuca cień o długości 11 m, a o tej samej porze cień chłopca o wzroście 170 cm ma długość 2,2 m. Oblicz wysokość drzewa.

Ukryj Podobne zadania

Wieża rzuca cień o długości 31,5m. W tym samym czasie wbity pionowo w ziemię pręt o wysokości 1,6m rzuca cień o długości 1,2m. Oblicz wysokość wieży.

Ania układa szklane kulki w ﬁgury pokazane na rysunku, na którym pokazane są pierwsze trzy ﬁgury.

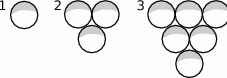
Niech 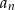będzie różnicą liczby kulek w 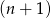–ej i –tej ﬁgurze. Wypisz pierwszych 5 wyrazów ciągu .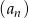
Uzasadnij, że 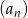jest ciągiem arytmetycznym i oblicz ile potrzeba kulek do ułożenia 20 ﬁgury.

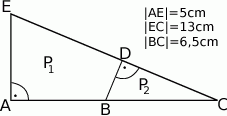
Mamy dwa pojemniki: pierwszy ma kształt sześcianu, drugi - ostrosłupa prawidłowego czworokątnego. Przekątna sześcianu ma długość 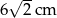√ -- 6 2 cm . Wysokość ostrosłupa tworzy ze ścianą boczną kąt o mierze 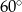60∘ . Pole powierzchni bocznej ostrosłupa jest równe 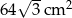√ -- 2 64 3 cm . Sprawdź na podstawie odpowiednich obliczeń, czy woda wypełniająca całkowicie pierwszy pojemnik zmieści się w drugim pojemniku.

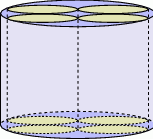
Puszki z napojami chłodzącymi pakuje się w ramach promocji do kartonowych pudełek w kształcie walca. Średnica zewnętrzna puszki wynosi 8 cm, a jej wysokość 15 cm. Jaka jest minimalna objętość pudełka zawierającego cztery puszki? Wynik podaj z dokładnością do 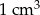1 cm 3 .

Taras znajduje się na wysokości 9 m i 35 cm nad powierzchnią ziemi. Schody prowadzące na taras z ostały tak zaprojektowane, że wysokość pierwszego stopnia jest równa 32 cm, a każdy następny stopień jest o 0,5 cm niższy od poprzedniego. Ile stopni mają te schody?

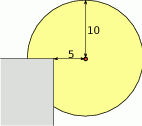
Latarnię uliczną umieszczono w odległości 5 m od naroża budynku – tak jak jest to pokazane na rysunku. Wiedząc, że światło latarni oświetla obszar w promieniu 10 m od źródła światła, oblicz jakie jest pole obszaru oświetlanego latarnią.

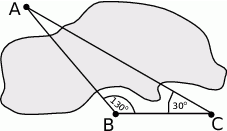
Obiekty 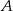i 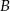leżą po dwóch stronach jeziora. W terenie dokonano pomiarów odpowiednich kątów i ich wyniki przedstawiono na rysunku. Odległość między obiektam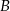i i 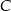jest równa 400 m. Oblicz odległość w linii prostej między obiektam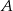i i 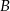i podaj wynik, zaokrąglając go do jednego metra.

Państwo Nowakowie przeznaczyli 26000 zł na zakup działki. Do jednej z ofert dołączono rysunek w skali 1:1000 dwóch przylegających do siebie działek. Jeden metr kwadratowy gruntu w tej ofercie kosztuje 35 zł. Oblicz, czy przeznaczona przez państwa Nowaków kwota wystarczy na zakup działki P 2 .

W wyniku tzw. złotego podziału odcinka otrzymuje się dwa nowe odcinki o tej własności, że stosunek krótszego z nich do dłuższego jest równy stosunkowi dłuższego z nich do całego odcinka. Dokonano złotego podziału odcinka o długości 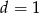d = 1 , oblicz długość krótszej części.

Poziome ramię szlabanu kolejowego o długości 4 m umieszczone jest na wysokości 1 m nad ziemią. Ramię szlabanu podnoszone jest pod kątem 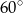60∘ do poziomu. Na jakiej wysokości znajduje się ramię szlabanu, gdy zostanie podniesiony? Wynik podaj z dokładnością do 0,1 m.

Metalowy stożek, którego tworząca o długości 10 jest nachylona do płaszczyzny podstawy pod kątem 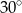30 ∘ , przetopiono na sześć jednakowych kulek. Oblicz promień kulki.

Akwarium o wymiarach 50 cm, 20 cm i wysokości 30 cm wypełnione jest do połowy wodą. O ile centymetrów podniesie się jej poziom, jeśli dolejemy 3 litry wody? Ile jeszcze litrów wody należy dolać do akwarium, aby wypełnić je w 3/4 objętości?

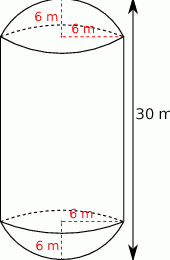
Elewator na zboże ma kształt walca który u podstaw ma doczepione półsfery. Średnica podstawy tego walca jest równa 12 m, a wysokość dachu wynosi 30 m. Oblicz, ile metrów kwadratowych blachy potrzeba na zbudowanie takiego elewatora. Wynik zaokrąglij do 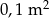0 ,1 m 2 .

Z metalowej rury wycięto dwa walce o tym samym promieniu podstawy. Objętość pierwszego z walców jest równa 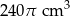240π cm 3 , a drugi walec jest wyższy od pierwszego o 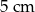5 cm i ma objętość większą o 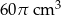60π cm 3 . Oblicz wysokości obu walców.

Wódz indiański wysłał trzech zwiadowców na zachód, północ i wschód. Każdy z nich oddalił się o 5 km od obozu i miał w zasięgu wzroku teren o promieniu 5 km.

Jaki obszar kontrolują zwiadowcy?
O ile zmniejszy się kontrolowany teren, jeśli jeden ze zwiadowców zostanie pojmany przez wrogie plemię? (Rozpatrz dwa przypadki)

Strona 2 z 3