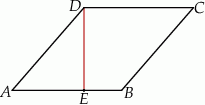
Wysokość 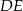 rombu
rombu 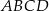 dzieli bok
dzieli bok 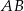 tego rombu tak, że
tego rombu tak, że 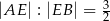 (zobacz rysunek).
(zobacz rysunek).
Oblicz wartość wyrażenia
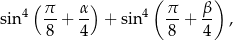
gdzie  i
i 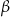 są dwoma sąsiednimi kątami wewnętrznymi rombu
są dwoma sąsiednimi kątami wewnętrznymi rombu 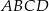 .
.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Wysokość 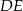 rombu
rombu 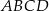 dzieli bok
dzieli bok 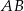 tego rombu tak, że
tego rombu tak, że 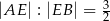 (zobacz rysunek).
(zobacz rysunek).

Oblicz wartość wyrażenia
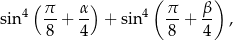
gdzie  i
i 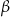 są dwoma sąsiednimi kątami wewnętrznymi rombu
są dwoma sąsiednimi kątami wewnętrznymi rombu  .
.
Na kole opisany jest romb. Stosunek pola koła do pola powierzchni rombu wynosi  . Wyznacz miarę kąta ostrego rombu.
. Wyznacz miarę kąta ostrego rombu.
Długość boku rombu jest równa  , a długości jego przekątnych są równe
, a długości jego przekątnych są równe 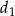 i
i 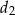 . Oblicz miarę kąta ostrego rombu jeżeli wiadomo, że
. Oblicz miarę kąta ostrego rombu jeżeli wiadomo, że 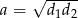 .
.
Długość boku rombu 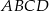 jest średnią geometryczną długości jego przekątnych. Oblicz miarę kąta ostrego tego rombu.
jest średnią geometryczną długości jego przekątnych. Oblicz miarę kąta ostrego tego rombu.
Znaleźć kąt ostry rombu, jeżeli wiadomo, że jego pole jest równe 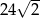 , a promień okręgu w niego wpisanego równy
, a promień okręgu w niego wpisanego równy 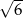 .
.
Stosunek pola rombu do pola koła wpisanego w ten romb wynosi 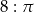 . Oblicz miarę kąta ostrego rombu.
. Oblicz miarę kąta ostrego rombu.
Dany jest romb 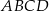 o boku długości 26, w którym przekątna
o boku długości 26, w którym przekątna 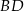 ma długość równą 20. Punkt
ma długość równą 20. Punkt 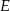 jest środkiem boku
jest środkiem boku 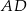 (zobacz rysunek).
(zobacz rysunek).
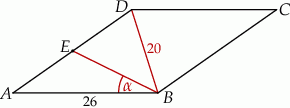
Oblicz sinus kąta  , jaki odcinek
, jaki odcinek 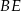 tworzy z bokiem
tworzy z bokiem 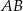 rombu
rombu 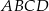 .
.
