Wykaż, że jeżeli ciąg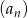 
jest ciągiem geometrycznym o wyrazach dodatnich, to ciąg o wyrazie ogólnym 
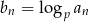, dla 
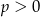i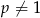 
jest ciągiem arytmetycznym.
/Szkoła średnia/Ciągi/Arytmetyczny i geometryczny/Na dowodzenie
Wykaż, że jeżeli ciąg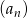 
jest arytmetyczny, to ciąg 
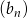określony wzorem 
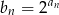jest geometryczny.
Na wykresie funkcji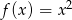 
wybrano trzy różne punkty, których odcięte są kolejnymi wyrazami ciągu arytmetycznego, a rzędne kolejnymi wyrazami ciągu geometrycznego. Wykaż, że odcięta co najmniej jednego z tych punktów jest liczbą niewymierną.
Wykaż, że trójkąt, którego długości boków są trzema kolejnymi wyrazami ciągu geometrycznego, miary kątów zaś trzema kolejnymi wyrazami ciągu arytmetycznego jest trójkątem równobocznym.
Udowodnij, że jeżeli ciąg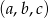 
jest jednocześnie arytmetyczny i geometryczny to 
.
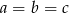Wykaż, że jeżeli liczby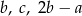 
są kolejnymi wyrazami ciągu geometrycznego to liczby 
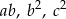są kolejnymi wyrazami ciągu arytmetycznego.
