Punkt 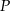 , będący punktem wewnętrznym trójkąta
, będący punktem wewnętrznym trójkąta 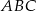 , przekształcamy przez symetrię względem prostych zawierających boki
, przekształcamy przez symetrię względem prostych zawierających boki 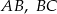 i
i 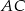 otrzymując odpowiednio punkty
otrzymując odpowiednio punkty 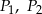 i
i 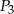 . Udowodnij, że pole sześciokąta
. Udowodnij, że pole sześciokąta 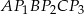 jest dwa razy większe od pola trójkąta
jest dwa razy większe od pola trójkąta 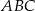 .
.
/Szkoła średnia/Geometria/Planimetria/Wielokąty/Sześciokąt
Na sześciokącie foremnym opisano okrąg i w ten sześciokąt wpisano okrąg. Pole powstałego pierścienia jest równe 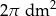 . Oblicz pole powierzchni wielokąta.
. Oblicz pole powierzchni wielokąta.
Pole koła wpisanego w sześciokąt foremny wynosi 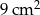 . Oblicz pole koła opisanego na tym sześciokącie.
. Oblicz pole koła opisanego na tym sześciokącie.
Ukryj
Podobne zadania
Pole koła wpisanego w sześciokąt foremny wynosi 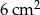 . Oblicz pole koła opisanego na tym sześciokącie.
. Oblicz pole koła opisanego na tym sześciokącie.
Oblicz długości przekątnych sześciokąta foremnego o boku 1.
Oblicz pole sześciokąta foremnego o boku długości 2.
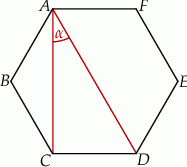
Oblicz miarę kąta  jaki tworzą przekątne
jaki tworzą przekątne 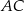 i
i  sześciokąta foremnego.
sześciokąta foremnego.
W sześciokącie foremnym połączono środki sąsiednich boków otrzymując ponownie sześciokąt foremny. Oblicz stosunek pól: otrzymanego i wyjściowego sześciokąta.

