Zadania.info Największy internetowy zbiór zadań z matematyki

/Szkoła średnia/Funkcje - wykresy/Wartość bezwzględna/Z logarytmiczną

Wyszukiwanie zadań

Dziedziną funkcji 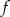f opisanej wzorem 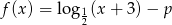f (x) = log 12(x+ 3)− p jest przedział 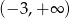(− 3,+ ∞ ) . Wiedząc, że do wykresu funkcji 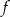f należy punkt 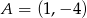A = (1,− 4) , oblicz wartość parametru 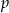p . Następnie:

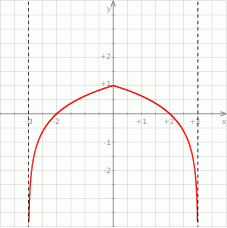
  • naszkicuj wykres funkcji g (x) = |f(x)| ;
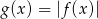  • wyznacz zbiór wszystkich wartości parametru 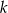k , dla których równanie 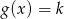g(x) = k ma dwa rozwiązania różnych znaków.
Ukryj Podobne zadania

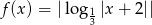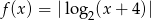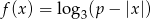Na rysunku przedstawiony jest fragment wykresu funkcji określonej wzorem f (x) = log3(p − |x|) .

PIC

  • Podaj wartość p .
  • Naszkicuj wykres funkcji y = |f(x )| .
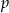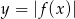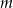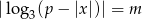  • Podaj w zależności od parametru m liczbę rozwiązań równania |log3(p − |x|)| = m .

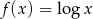Dana jest funkcja f(x ) = lo gx .

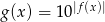  • Naszkicuj wykres funkcji g(x) = 10|f(x)| .
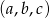  • Udowodnij, że jeżeli (a,b,c) jest ciągiem geometrycznym o wyrazach dodatnich to 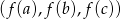(f(a),f(b ),f (c)) jest ciągiem arytmetycznym.