Zadania.info Największy internetowy zbiór zadań z matematyki

/Szkoła średnia/Funkcje - wykresy/Parabola/Wzór z wykresu/1 niewiadoma

Wyszukiwanie zadań

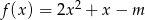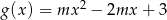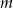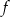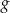Dane są funkcje 2 f(x) = 2x + x− m i 2 g (x) = mx − 2mx + 3 . Dla jakich wartości parametru m wykresy funkcji f i g przecinają się w dwóch punktach, których odcięte mają różne znaki?

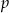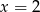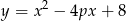Dla jakiego p prosta o równaniu x = 2 jest osią symetrii wykresu funkcji y = x2 − 4px + 8 .

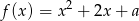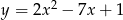Wyznacz te wartości współczynnika a , dla których wierzchołek paraboli, będącej wykresem funkcji f(x) = x2 + 2x+ a , należy do paraboli o równaniu y = 2x2 − 7x + 1 .

Funkcja 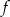f określona jest wzorem 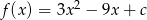2 f(x ) = 3x − 9x + c , gdzie 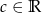c ∈ R . Wyznacz wszystkie wartości współczynnika c , dla których:

  • jednym z miejsc zerowych funkcji 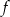f jest liczba 2;
  • wierzchołek paraboli, która jest wykresem funkcji 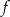f , należy do prostej o równaniu y = x .

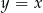Dana jest funkcja 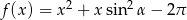2 2 f(x ) = x + xsin α− 2π , dla α ∈ ⟨0,2π ⟩ .

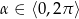  • Wyznacz wszystkie wartości parametru α , dla których osią symetrii wykresu tej funkcji jest prosta x = − 1 2 .
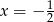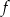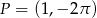  • Wykaż, że nie istnieje taka wartość parametru α , dla której do wykresu funkcji f należy punkt P = (1,− 2π ) .