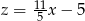Granica 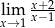
A) jest równa 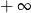 B) nie istnieje C) jest liczbą rzeczywistą D) jest równa
B) nie istnieje C) jest liczbą rzeczywistą D) jest równa 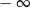
/Szkoła średnia/Zadania testowe
Granica 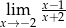
A) jest równa 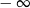 B) jest równa
B) jest równa 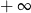 C) jest liczbą rzeczywistą D) nie istnieje
C) jest liczbą rzeczywistą D) nie istnieje
Granica 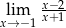
A) jest równa 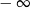 B) jest liczbą rzeczywistą C) jest równa
B) jest liczbą rzeczywistą C) jest równa 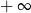 D) nie istnieje
D) nie istnieje
Granica 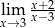
A) jest równa 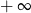 B) jest równa
B) jest równa 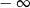 C) jest liczbą rzeczywistą D) nie istnieje
C) jest liczbą rzeczywistą D) nie istnieje
Granica 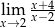
A) jest liczbą rzeczywistą B) jest równa 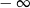 C) nie istnieje D) jest równa
C) nie istnieje D) jest równa 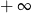
Granica 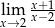
A) jest równa 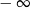 B) nie istnieje C) jest liczbą rzeczywistą D) jest równa
B) nie istnieje C) jest liczbą rzeczywistą D) jest równa 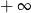
Granica 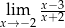
A) nie istnieje B) jest równa 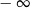 C) jest liczbą rzeczywistą D) jest równa
C) jest liczbą rzeczywistą D) jest równa 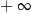
Granica 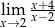
A) jest liczbą rzeczywistą B) jest równa 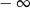 C) nie istnieje D) jest równa
C) nie istnieje D) jest równa 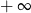
Kąt  jest kątem ostrym takim, że
jest kątem ostrym takim, że 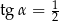 . Zatem
. Zatem
A) 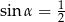 i
i 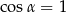 B)
B) 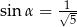 i
i 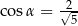
C) 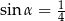 i
i 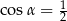 D)
D) 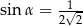 i
i 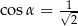
Kąt  jest kątem ostrym takim, że
jest kątem ostrym takim, że 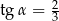 . Zatem
. Zatem
A) 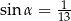 i
i 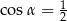 B)
B) 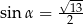 i
i 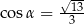
C) 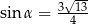 i
i 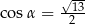 D)
D) 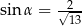 i
i 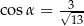
Jeśli 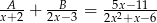 , to suma
, to suma 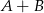 jest równa
jest równa
A) 0 B) 2 C) 1 D) 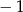
Ile wynosi 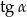 jeśli
jeśli 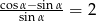 ?
?
A) 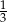 B) 3 C)
B) 3 C) 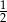 D) 2
D) 2
Jeżeli 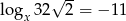 to liczba
to liczba  jest równa
jest równa
A) 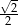 B)
B) 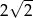 C)
C) 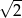 D) 2
D) 2
Jeżeli 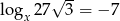 to liczba
to liczba  jest równa
jest równa
A) 3 B) 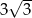 C)
C) 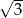 D)
D) 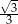
Z cyfr 1, 2, 3, 4, 5, 6 tworzymy sześciocyfrowe liczby o niepowtarzających się cyfrach w taki sposób, że cyfry parzyste zapisane są obok siebie. Powstało w ten sposób
A) 36 liczb B) 132 liczby C) 144 liczby D) 720 liczb
Suma liczby odwrotnej do 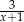 i przeciwnej do
i przeciwnej do 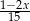 jest równa
jest równa
A) 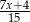 B)
B) 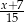 C)
C) 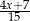 D)
D) 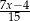
Do 2 kg roztworu soli o stężeniu 20% dosypano pół kilograma soli. Stężenie procentowe nowego roztworu wynosi
A) 27% B) 40% C) 30% D) 36%
Do 2 kg roztworu soli o stężeniu 20% dosypano 1,2 kilograma soli. Stężenie procentowe nowego roztworu wynosi
A) 80% B) 50% C) 60% D) 70%
Do 2 kg roztworu soli o stężeniu 20% dosypano 560 gram soli. Stężenie procentowe nowego roztworu wynosi
A) 37,5% B) 40% C) 43,5% D) 36%
Do 4 kg roztworu soli o stężeniu 10% dosypano pół kilograma soli. Stężenie procentowe nowego roztworu wynosi
A) 22,5% B) 40% C) 20% D) 36%
Wartość wyrażenia 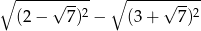 jest równa
jest równa
A) -1 B) -5 C) 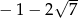 D)
D) 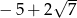
Liczba 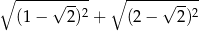 jest równa
jest równa
A) 1 B) 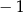 C)
C) 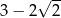 D)
D) 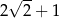
Liczba 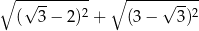 jest równa
jest równa
A) 1 B) 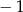 C)
C) 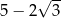 D)
D) 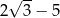
Wartość wyrażenia 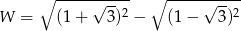 jest równa
jest równa
A) 0 B) 2 C) 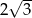 D)
D) 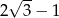
Funkcja 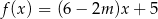 jest rosnąca wtedy i tylko wtedy, gdy
jest rosnąca wtedy i tylko wtedy, gdy
A) 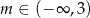 B)
B) 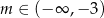 C)
C) 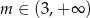 D)
D) 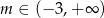
Funkcja liniowa 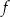 jest określona wzorem
jest określona wzorem 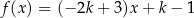 , gdzie
, gdzie 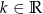 . Funkcja
. Funkcja 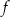 jest malejąca dla każdej liczby
jest malejąca dla każdej liczby 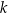 należącej do przedziału
należącej do przedziału
A) 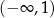 B)
B) 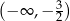 C)
C) 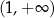 D)
D) 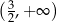
Funkcja 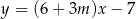 jest rosnąca wtedy i tylko wtedy, gdy
jest rosnąca wtedy i tylko wtedy, gdy
A) 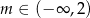 B)
B) 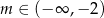 C)
C) 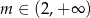 D)
D) 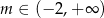
Funkcja 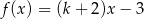 jest malejąca jeśli
jest malejąca jeśli
A) 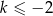 B)
B) 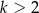 C)
C) 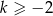 D)
D) 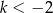
Funkcja 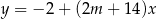 jest rosnąca wtedy i tylko wtedy, gdy
jest rosnąca wtedy i tylko wtedy, gdy
A) 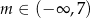 B)
B) 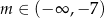 C)
C) 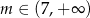 D)
D) 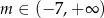
Funkcja 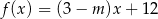 jest malejąca, gdy
jest malejąca, gdy
A) 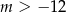 B)
B) 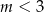 C)
C) 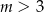 D)
D) 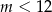
Funkcja liniowa 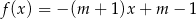 jest rosnąca dla
jest rosnąca dla
A) 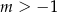 B)
B) 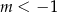 C)
C) 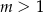 D)
D) 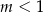
Funkcja 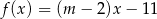 jest rosnąca, gdy
jest rosnąca, gdy
A) 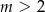 B)
B) 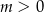 C)
C) 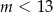 D)
D) 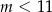
Cena pewnego towaru wraz z 7–procentowym podatkiem VAT jest równa 34 347 zł. Cena tego samego towaru wraz z 23–procentowym podatkiem VAT będzie równa
A) 37 236 zł B) 39 842,52 zł C) 39 483 zł D) 42 246,81 zł
Cena towaru z 22% podatkiem VAT wynosi 183 zł. Cena tego towaru z 7% podatkiem VAT jest równa
A) 160,50 zł B) 195,81 zł C) 210,45 zł D) 223,26 zł
Ciąg 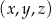 jest geometryczny. Iloczyn wszystkich wyrazów tego ciągu jest równy 64. Stąd wynika, że
jest geometryczny. Iloczyn wszystkich wyrazów tego ciągu jest równy 64. Stąd wynika, że 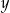 jest równe
jest równe
A) 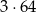 B)
B) 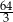 C) 4 D) 3
C) 4 D) 3
Ciąg 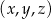 jest geometryczny. Iloczyn wszystkich wyrazów tego ciągu jest równy 27. Stąd wynika, że
jest geometryczny. Iloczyn wszystkich wyrazów tego ciągu jest równy 27. Stąd wynika, że 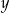 jest równe
jest równe
A) 81 B) 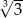 C) 9 D) 3
C) 9 D) 3
Na rysunku przedstawiono fragment wykresu funkcji kwadratowej 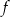 . Jednym z miejsc zerowych tej funkcji jest liczba 2. Do wykresu funkcji
. Jednym z miejsc zerowych tej funkcji jest liczba 2. Do wykresu funkcji 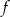 należy punkt
należy punkt 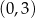 . Prosta o równaniu
. Prosta o równaniu 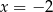 jest osią symetrii paraboli, będącej wykresem funkcji
jest osią symetrii paraboli, będącej wykresem funkcji 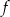 .
.
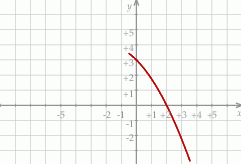
Drugim miejscem zerowym funkcji 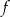 jest liczba
jest liczba
A) 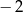 B)
B) 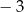 C)
C) 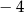 D)
D) 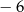
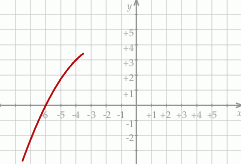
Na rysunku przedstawiono fragment wykresu funkcji kwadratowej 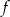 . Jednym z miejsc zerowych tej funkcji jest liczba
. Jednym z miejsc zerowych tej funkcji jest liczba 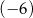 . Do wykresu funkcji
. Do wykresu funkcji 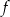 należy punkt
należy punkt 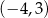 . Prosta o równaniu
. Prosta o równaniu 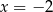 jest osią symetrii paraboli, będącej wykresem funkcji
jest osią symetrii paraboli, będącej wykresem funkcji 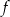 .
.
Drugim miejscem zerowym funkcji 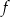 jest liczba
jest liczba
A) 2 B) 1 C) 0 D) 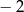
Punkty 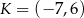 i
i 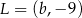 są końcami odcinka
są końcami odcinka 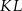 . Pierwsza współrzędna środka odcinka
. Pierwsza współrzędna środka odcinka 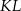 jest o 3 większa od jego drugiej współrzędnej. Wynika stąd, że
jest o 3 większa od jego drugiej współrzędnej. Wynika stąd, że
A) 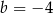 B)
B) 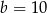 C)
C) 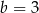 D)
D) 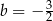
Liczba 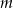 , dla której rozwiązaniem równania
, dla której rozwiązaniem równania 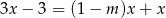 jest
jest 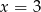 wynosi
wynosi
A) 3 B) 2 C) 1 D) 0
Rozwiązaniem równania 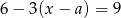 z niewiadomą
z niewiadomą  jest liczba 2. Zatem
jest liczba 2. Zatem
A) 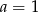 B)
B) 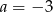 C)
C) 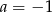 D)
D) 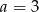
Liczba 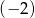 jest pierwiastkiem równania
jest pierwiastkiem równania 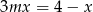 . Wtedy
. Wtedy
A) 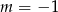 B)
B) 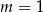 C)
C) 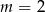 D)
D) 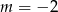
W tabeli podano dane dotyczące wyników z pracy klasowej z matematyki uzyskanych w pewnej klasie.
| Liczba uczniów | 3 | 6 | 8 | 4 | 4 | 2 |
| Ocena | 1 | 2 | 3 | 4 | 5 | 6 |
Różnica średniej arytmetycznej ocen i mediany wynosi
A) 0,2 B)  C)
C) 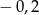 D)
D) 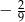
W tabeli podano dane dotyczące wyników z pracy klasowej z matematyki uzyskanych w pewnej klasie.
| Liczba uczniów | 2 | 4 | 7 | 2 | 3 | 2 |
| Ocena | 1 | 2 | 3 | 4 | 5 | 6 |
Różnica średniej arytmetycznej ocen i mediany wynosi
A) 0,3 B) 3,3 C) 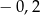 D) 3
D) 3
W tabeli podano dane dotyczące wyników z pracy klasowej z matematyki uzyskanych w pewnej klasie.
| Liczba uczniów | 5 | 3 | 5 | 7 | 3 | 1 |
| Ocena | 1 | 2 | 3 | 4 | 5 | 6 |
Różnica średniej arytmetycznej ocen i mediany wynosi
A) 3,125 B) 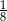 C) 1,125 D)
C) 1,125 D) 
Przybliżona długość przeciwprostokątnej trójkąta prostokątnego przedstawionego na rysunku jest równa

A) 5,49 B) 5,9 C) 5,85 D) 5,5
Z przeciwległych wierzchołków kwadratu o boku 1 zatoczono koła o promieniu 1. Pole części wspólnej tych kół jest równe
A) 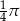 B)
B) 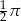 C)
C) 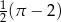 D)
D) 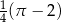
Z przeciwległych wierzchołków kwadratu o boku 2 zatoczono koła o promieniu 2. Pole części wspólnej tych kół jest równe
A) 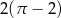 B)
B) 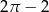 C)
C) 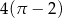 D)
D) 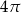
Cięciwa dzieli okrąg na dwa łuki w stosunku 5:7. Miara kąta wpisanego opartego na krótszym łuku okręgu jest równa
A) 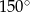 B)
B) 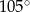 C)
C) 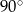 D)
D) 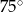
Liczby  i
i  są dodatnie. Liczba
są dodatnie. Liczba 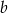 stanowi 48% liczby
stanowi 48% liczby  oraz 32% liczby
oraz 32% liczby  . Wynika stąd, że
. Wynika stąd, że
A) 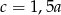 B)
B) 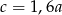 C)
C) 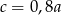 D)
D) 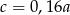
Liczby  i
i  są dodatnie. Liczba
są dodatnie. Liczba 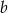 stanowi 42% liczby
stanowi 42% liczby  oraz 56% liczby
oraz 56% liczby  . Wynika stąd, że
. Wynika stąd, że
A) 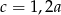 B)
B) 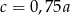 C)
C) 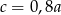 D)
D) 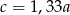
Liczba 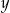 jest o 120% większa od dodatniej liczby
jest o 120% większa od dodatniej liczby  , a liczba
, a liczba  jest pięciokrotnie mniejsza od liczby
jest pięciokrotnie mniejsza od liczby 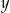 . Zatem
. Zatem
A) 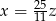 B)
B) 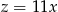 C)
C) 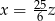 D)
D)