Cena towaru bez podatku VAT wynosi 180 zł. Ten sam towar wraz z podatkiem VAT i 5% rabatem handlowym kosztuje 184,68 zł. Jaką stawką VAT opodatkowano ten towar?
A) 5% B) 8% C) 23% D) 108%
/Szkoła średnia/Zadania testowe
Cena towaru bez podatku VAT wynosi 240 zł. Ten sam towar wraz z podatkiem VAT i 8% rabatem handlowym kosztuje 231,84 zł. Jaką stawką VAT opodatkowano ten towar?
A) 5% B) 8% C) 23% D) 105%
Punkty 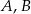 i
i 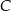 leżą na okręgu o środku
leżą na okręgu o środku 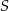 (zobacz rysunek).
(zobacz rysunek).
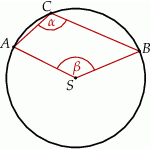
Miary  i
i 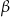 zaznaczonych kątów
zaznaczonych kątów 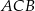 i
i 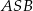 spełniają warunek
spełniają warunek 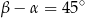 . Wynika stąd, że
. Wynika stąd, że
A) 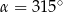 B)
B) 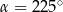 C)
C) 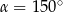 D)
D) 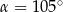
Układ liczb 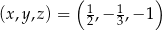 jest rozwiązaniem układu równań
jest rozwiązaniem układu równań
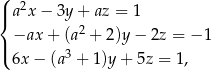
dla
A) 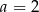 B)
B) 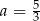 C)
C) 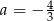 D)
D) 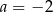
W pewnej klasie stosunek liczby dziewcząt do liczby chłopców jest równy 4:5. Losujemy jedną osobę z tej klasy. Prawdopodobieństwo tego, że będzie to dziewczyna, jest równe
A) 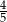 B)
B)  C)
C) 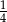 D)
D) 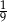
Pewne przedsiębiorstwo postanowiło przyznać każdemu pracownikowi losowy 5-cyfrowy identyfikator, przy czym ustalono, że w identyfikatorze nie może występować cyfra 0. Prawdopodobieństwo 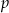 otrzymania identyfikatora, w którym każde dwie cyfry są różne spełnia warunek
otrzymania identyfikatora, w którym każde dwie cyfry są różne spełnia warunek
A) 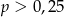 B)
B) 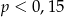 C)
C) 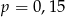 D)
D) 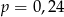
Magda wydała na książkę połowę kwoty otrzymanej od mamy, a za 40% tego, co jej zostało, kupiła bilet do kina. Ile procent kwoty otrzymanej od mamy pozostało Magdzie?
A) 30% B) 60% C) 10% D) 20%
Andrzej połowę kwoty otrzymanej od taty przeznaczył na nową kurtkę, a 20% tego, co mu pozostało przeznaczył na bilet do kina. Ile procent kwoty otrzymanej od taty pozostało Andrzejowi?
A) 30% B) 80% C) 40% D) 20%
Suma długości wszystkich przekątnych sześcianu jest równa 24. Pole powierzchni całkowitej tego sześcianu jest równe
A) 144 B) 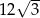 C) 36 D) 72
C) 36 D) 72
Suma dwóch początkowych wyrazów ciągu arytmetycznego 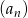 wynosi 5, a trzeci wyraz jest równy 7. Wówczas
wynosi 5, a trzeci wyraz jest równy 7. Wówczas
A) 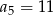 B)
B) 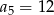 C)
C) 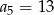 D)
D) 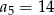
Suma dwóch początkowych wyrazów ciągu arytmetycznego 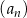 wynosi 7, a trzeci wyraz jest równy 5. Wówczas
wynosi 7, a trzeci wyraz jest równy 5. Wówczas
A) 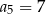 B)
B) 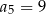 C)
C) 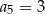 D)
D) 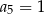
Wyrażenie 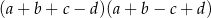 może być zapisane w postaci
może być zapisane w postaci
A) 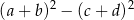 B)
B) 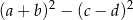
C) 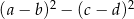 D)
D) 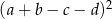
Wyrażenie 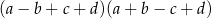 może być zapisane w postaci
może być zapisane w postaci
A) 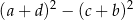 B)
B) 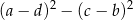
C) 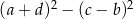 D)
D) 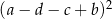
Liczba 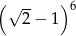 jest równa
jest równa
A) 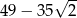 B)
B) 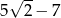 C)
C) 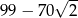 D)
D) 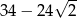
Pole powierzchni całkowitej graniastosłupa prawidłowego czworokątnego, w którym wysokość jest 3 razy dłuższa od krawędzi podstawy, jest równe 140. Zatem krawędź podstawy tego graniastosłupa jest równa
A) 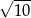 B)
B) 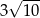 C)
C) 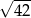 D)
D) 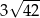
Pole powierzchni całkowitej graniastosłupa prawidłowego czworokątnego, w którym wysokość jest 3 razy krótsza od krawędzi podstawy, jest równe 60. Zatem krawędź podstawy tego graniastosłupa jest równa
A) 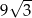 B)
B) 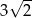 C)
C) 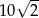 D)
D) 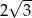
Na rysunku przedstawiono fragment wykresu funkcji kwadratowej 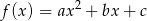 , której miejsca zerowe to:
, której miejsca zerowe to: 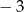 i 1.
i 1.
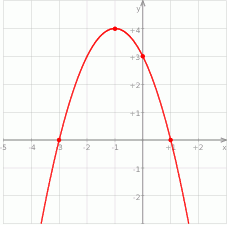
Współczynnik  we wzorze funkcji
we wzorze funkcji 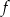 jest równy
jest równy
A) 1 B) 2 C) 3 D) 4
Na rysunku przedstawiono fragment wykresu funkcji kwadratowej 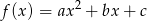 , której miejsca zerowe to:
, której miejsca zerowe to: 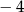 i 2.
i 2.
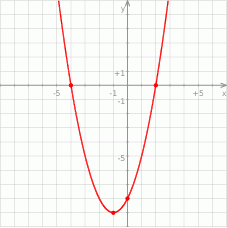
Współczynnik  we wzorze funkcji
we wzorze funkcji 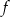 jest równy
jest równy
A) 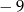 B)
B) 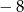 C) 4 D)
C) 4 D) 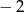
Jeżeli 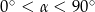 oraz
oraz 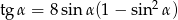 , to
, to
A) 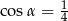 B)
B) 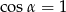 C)
C) 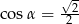 D)
D) 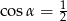
Jeżeli 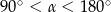 oraz
oraz 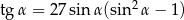 , to
, to
A) 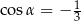 B)
B) 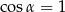 C)
C) 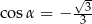 D)
D) 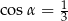
Równanie 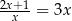
A) ma dwa rozwiązania: 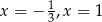 B) ma dwa rozwiązania:
B) ma dwa rozwiązania: 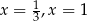
C) nie ma żadnego rozwiązania D) ma tylko jedno rozwiązanie 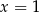
Rozwiązaniem równania 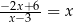 jest
jest
A) 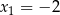 B)
B) 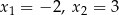 C)
C) 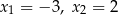 D)
D) 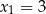
Równanie 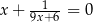
A) ma dokładnie dwa rozwiązania rzeczywiste.
B) ma dokładnie trzy rozwiązania rzeczywiste.
C) ma dokładnie jedno rozwiązanie rzeczywiste.
D) nie ma rozwiązań.
Równanie 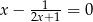
A) ma dokładnie dwa rozwiązania rzeczywiste.
B) ma dokładnie trzy rozwiązania rzeczywiste.
C) ma dokładnie jedno rozwiązanie rzeczywiste.
D) nie ma rozwiązań.
Równanie 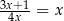
A) ma dwa rozwiązania: 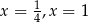 B) ma dwa rozwiązania:
B) ma dwa rozwiązania: 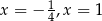
C) ma dwa rozwiązania: 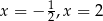 D) ma tylko jedno rozwiązanie
D) ma tylko jedno rozwiązanie 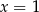
Ile jest wszystkich liczb pięciocyfrowych, większych 43080, utworzonych wyłącznie z cyfr 1, 2, 3, 4 przy założeniu, że cyfry mogą się powtarzać, ale nie wszystkie z tych cyfr muszą być wykorzystane?
A) 48 B) 15 C) 128 D) 192
Ile jest wszystkich liczb pięciocyfrowych, większych 53079, utworzonych wyłącznie z cyfr 2, 3, 4, 5 przy założeniu, że cyfry mogą się powtarzać, ale nie wszystkie z tych cyfr muszą być wykorzystane?
A) 48 B) 15 C) 128 D) 192
Środkiem okręgu jest punkt 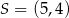 . Do okręgu należy punkt
. Do okręgu należy punkt 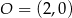 . Równanie tego okręgu to
. Równanie tego okręgu to
A) 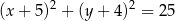 B)
B) 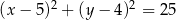
C) 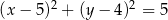 D)
D) 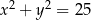
Środkiem okręgu jest punkt 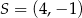 . Do okręgu należy punkt
. Do okręgu należy punkt 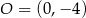 . Równanie tego okręgu to
. Równanie tego okręgu to
A) 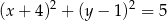 B)
B) 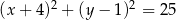
C) 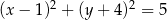 D)
D) 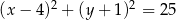
Środkiem okręgu jest punkt 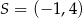 . Do okręgu należy punkt
. Do okręgu należy punkt 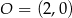 . Równanie tego okręgu to
. Równanie tego okręgu to
A) 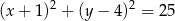 B)
B) 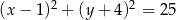
C) 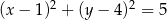 D)
D) 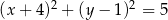
Punkt 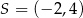 jest środkiem okręgu. Na okręgu leży punkt
jest środkiem okręgu. Na okręgu leży punkt 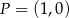 . Równanie tego okręgu ma postać
. Równanie tego okręgu ma postać
A) 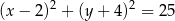 B)
B) 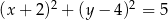
C) 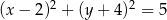 D)
D) 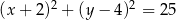
Dane są dwie proste równoległe 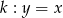 oraz
oraz 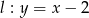 . Odległość między tymi prostymi jest równa:
. Odległość między tymi prostymi jest równa:
A) 2 B) 1,5 C) 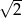 D) 1
D) 1
Odległość między prostymi 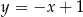 i
i 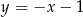 jest równa
jest równa
A) 2 B) 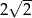 C) 1 D)
C) 1 D) 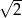
Dane są dwie proste równoległe 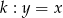 oraz
oraz 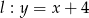 . Odległość między tymi prostymi jest równa:
. Odległość między tymi prostymi jest równa:
A) 4 B) 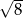 C)
C) 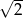 D) 3
D) 3
Dane są dwie proste równoległe 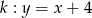 oraz
oraz 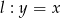 . Odległość między tymi prostymi jest równa:
. Odległość między tymi prostymi jest równa:
A) 2 B) 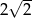 C)
C) 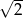 D) 4
D) 4
Liczba 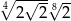 jest równa
jest równa
A) 2 B) 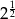 C)
C) 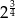 D)
D) 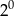
Liczba 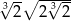 jest równa
jest równa
A) 2 B) 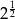 C)
C) 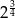 D)
D) 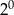
W kartezjańskim układzie współrzędnych 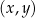 przedstawiono fragment wykresu funkcji kwadratowej
przedstawiono fragment wykresu funkcji kwadratowej 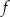 (zobacz rysunek). Wierzchołek paraboli, która jest wykresem funkcji
(zobacz rysunek). Wierzchołek paraboli, która jest wykresem funkcji 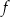 , oraz punkty przecięcia paraboli z osiami układu współrzędnych mają współrzędne całkowite.
, oraz punkty przecięcia paraboli z osiami układu współrzędnych mają współrzędne całkowite.
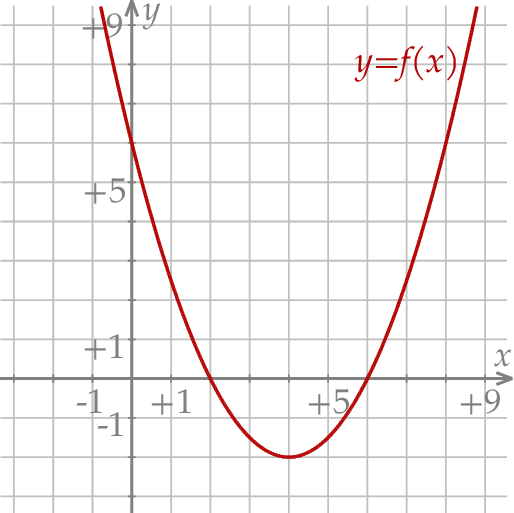
Dokończ zdanie. Wybierz dwie właściwe odpowiedzi spośród podanych.
Wzór funkcji 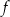 można przedstawić w postaci:
można przedstawić w postaci:
A) 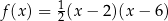 B)
B) 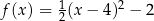
C) 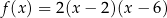 D)
D) 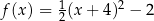
E) 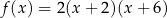 F)
F) 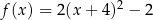
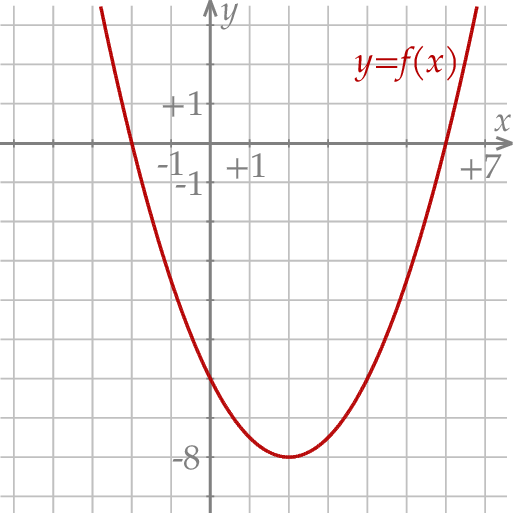
W kartezjańskim układzie współrzędnych 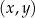 przedstawiono fragment wykresu funkcji kwadratowej
przedstawiono fragment wykresu funkcji kwadratowej 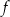 (zobacz rysunek). Wierzchołek paraboli, która jest wykresem funkcji
(zobacz rysunek). Wierzchołek paraboli, która jest wykresem funkcji 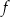 , oraz punkty przecięcia paraboli z osiami układu współrzędnych mają współrzędne całkowite.
, oraz punkty przecięcia paraboli z osiami układu współrzędnych mają współrzędne całkowite.
Dokończ zdanie. Wybierz dwie właściwe odpowiedzi spośród podanych.
Wzór funkcji 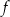 można przedstawić w postaci:
można przedstawić w postaci:
A) 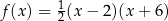 B)
B) 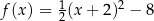
C) 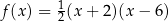 D)
D) 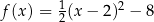
E) 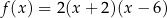 F)
F) 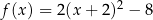
W kartezjańskim układzie współrzędnych 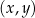 przedstawiono fragment wykresu funkcji kwadratowej
przedstawiono fragment wykresu funkcji kwadratowej 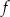 (zobacz rysunek). Wierzchołek paraboli, która jest wykresem funkcji
(zobacz rysunek). Wierzchołek paraboli, która jest wykresem funkcji 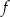 , oraz punkty przecięcia paraboli z osiami układu współrzędnych mają współrzędne całkowite.
, oraz punkty przecięcia paraboli z osiami układu współrzędnych mają współrzędne całkowite.
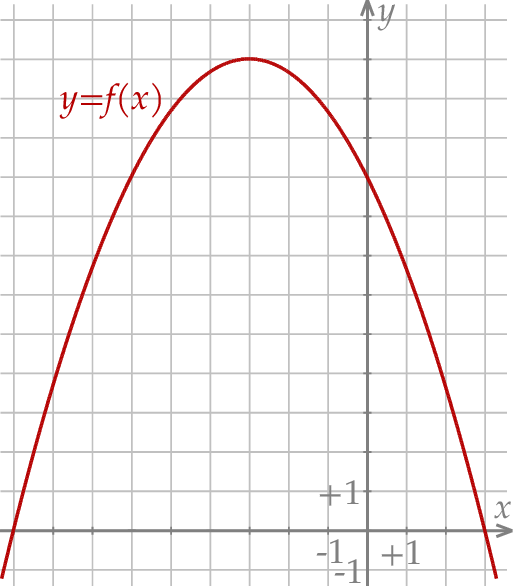
Dokończ zdanie. Wybierz dwie właściwe odpowiedzi spośród podanych.
Wzór funkcji 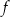 można przedstawić w postaci:
można przedstawić w postaci:
A) 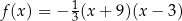 B)
B) 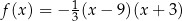
C) 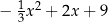 D)
D) 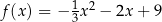
E) 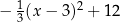 F)
F) 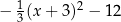
Granica 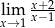
A) jest równa 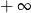 B) nie istnieje C) jest liczbą rzeczywistą D) jest równa
B) nie istnieje C) jest liczbą rzeczywistą D) jest równa 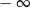
Granica 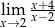
A) jest liczbą rzeczywistą B) jest równa 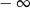 C) nie istnieje D) jest równa
C) nie istnieje D) jest równa 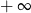
Granica 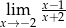
A) jest równa 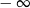 B) jest równa
B) jest równa 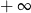 C) jest liczbą rzeczywistą D) nie istnieje
C) jest liczbą rzeczywistą D) nie istnieje
Granica 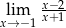
A) jest równa 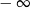 B) jest liczbą rzeczywistą C) jest równa
B) jest liczbą rzeczywistą C) jest równa 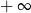 D) nie istnieje
D) nie istnieje
Granica 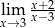
A) jest równa 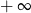 B) jest równa
B) jest równa 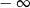 C) jest liczbą rzeczywistą D) nie istnieje
C) jest liczbą rzeczywistą D) nie istnieje
Granica 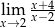
A) jest liczbą rzeczywistą B) jest równa 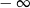 C) nie istnieje D) jest równa
C) nie istnieje D) jest równa 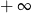
Granica 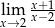
A) jest równa 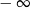 B) nie istnieje C) jest liczbą rzeczywistą D) jest równa
B) nie istnieje C) jest liczbą rzeczywistą D) jest równa 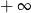
Granica 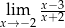
A) nie istnieje B) jest równa 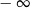 C) jest liczbą rzeczywistą D) jest równa
C) jest liczbą rzeczywistą D) jest równa