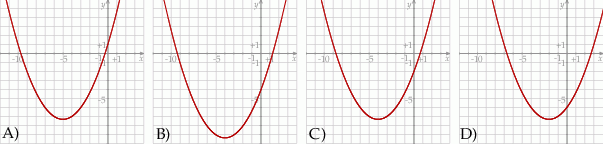
Funkcja 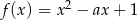 przyjmuje wartości mniejsze niż
przyjmuje wartości mniejsze niż 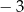 dla
dla
A) 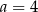 B)
B) 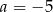 C)
C) 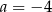 D)
D) 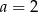
/Szkoła średnia/Zadania testowe
Liczba 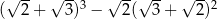 jest równa
jest równa
A) 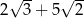 B)
B) 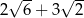 C)
C) 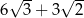 D)
D) 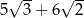
Liczba 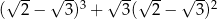 jest równa
jest równa
A) 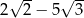 B)
B) 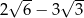 C)
C) 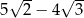 D)
D) 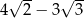
Dane są punkty 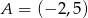 oraz
oraz 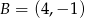 . Promień okręgu opisanego na trójkącie równobocznym
. Promień okręgu opisanego na trójkącie równobocznym 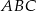 jest równy
jest równy
A) 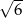 B)
B) 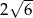 C)
C) 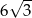 D)
D) 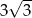
Punkty 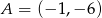 i
i 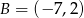 są wierzchołkami trójkąta równobocznego
są wierzchołkami trójkąta równobocznego 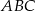 . Promień koła opisanego na tym trójkącie jest równy
. Promień koła opisanego na tym trójkącie jest równy
A) 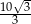 B)
B) 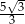 C)
C) 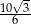 D)
D) 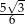
Punkty 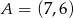 i
i 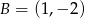 są wierzchołkami trójkąta równobocznego
są wierzchołkami trójkąta równobocznego 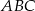 . Promień koła opisanego na tym trójkącie jest równy
. Promień koła opisanego na tym trójkącie jest równy
A) 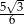 B)
B) 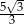 C)
C) 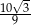 D)
D) 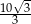
Dane są dwie urny z kulami, w każdej jest 5 kul. W pierwszej urnie jest jedna kula biała i 4 kule czarne. W drugiej urnie są 3 kule białe i 2 kule czarne. Rzucamy jeden raz symetryczną sześcienną kostką do gry. Jeśli wypadnie jedno lub dwa oczka, to losujemy jedną kulę z pierwszej urny, natomiast jeśli wypadną co najmniej trzy oczka, to losujemy jedną kulę z drugiej urny. Prawdopodobieństwo wylosowania kuli białej jest równe
A) 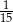 B)
B) 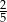 C)
C) 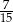 D)
D) 
Dane są dwie urny z kulami, w każdej jest 5 kul. W pierwszej urnie są dwie kule białe i 3 kule czarne. W drugiej urnie są 3 kule białe i 2 kule czarne. Rzucamy jeden raz symetryczną sześcienną kostką do gry. Jeśli wypadnie jedno lub dwa oczka, to losujemy jedną kulę z pierwszej urny, natomiast jeśli wypadną co najmniej trzy oczka, to losujemy jedną kulę z drugiej urny. Prawdopodobieństwo wylosowania kuli czarnej jest równe
A) 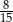 B)
B) 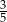 C)
C) 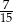 D)
D) 
Dane są dwie urny z kulami, w każdej jest 5 kul. W pierwszej urnie są dwie kule białe i 3 kule czarne. W drugiej urnie są 3 kule białe i 2 kule czarne. Rzucamy jeden raz symetryczną sześcienną kostką do gry. Jeśli wypadnie jedno lub dwa oczka, to losujemy jedną kulę z pierwszej urny, natomiast jeśli wypadną co najmniej trzy oczka, to losujemy jedną kulę z drugiej urny. Prawdopodobieństwo wylosowania kuli białej jest równe
A) 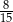 B)
B) 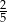 C)
C) 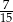 D)
D) 
Dane są dwie urny z kulami, w każdej jest 5 kul. W pierwszej urnie jest jedna kula biała i 4 kule czarne. W drugiej urnie są 3 kule białe i 2 kule czarne. Rzucamy jeden raz symetryczną sześcienną kostką do gry. Jeśli wypadnie jedno lub dwa oczka, to losujemy jedną kulę z pierwszej urny, natomiast jeśli wypadną co najmniej trzy oczka, to losujemy jedną kulę z drugiej urny. Prawdopodobieństwo wylosowania kuli czarnej jest równe
A) 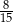 B)
B) 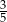 C)
C) 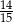 D)
D) 
Dane są dwie urny z kulami. W każdej z urn jest siedem kul. W pierwszej urnie są jedna kula biała i sześć kul czarnych, w drugiej urnie są cztery kule białe i trzy kule czarne. Rzucamy jeden raz symetryczną monetą. Jeżeli wypadnie reszka, to losujemy jedną kulę z pierwszej urny, w przeciwnym przypadku – jedną kulę z drugiej urny. Prawdopodobieństwo zdarzenia polegającego na tym, że wylosujemy kulę białą w tym doświadczeniu, jest równe
A) 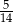 B)
B) 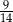 C)
C)  D)
D) 
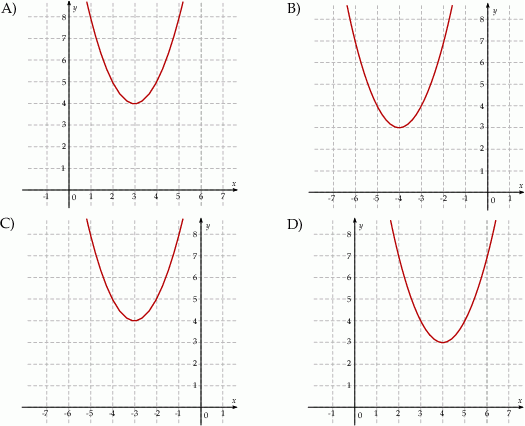
Na jednym z rysunków przedstawiono fragment wykresu funkcji kwadratowej określonej wzorem 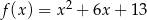 . Wskaż ten rysunek.
. Wskaż ten rysunek.
Wartość wyrażenia 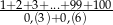 jest równa
jest równa
A) 505 B) 5050 C) 5000 D) 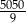
Wartość wyrażenia 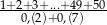 jest równa
jest równa
A) 1275 B) 2550 C) 1225 D) 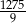
Wartość wyrażenia 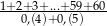 jest równa
jest równa
A) 3660 B) 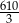 C) 1830 D) 1770
C) 1830 D) 1770
Na rysunku przedstawiono fragment wykresu funkcji kwadratowej 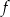 .
.
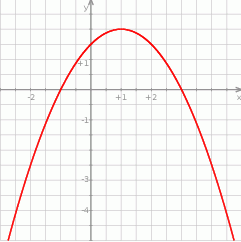
Funkcja 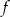 jest określona wzorem
jest określona wzorem
A) 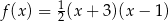 B)
B) 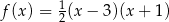
C) 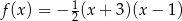 D)
D) 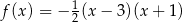
Na rysunku przedstawiono fragment wykresu funkcji kwadratowej 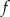 .
.
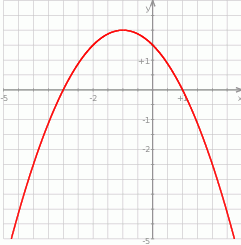
Funkcja 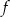 jest określona wzorem
jest określona wzorem
A) 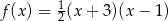 B)
B) 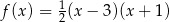
C) 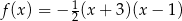 D)
D) 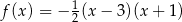
Dany jest ciąg geometryczny 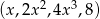 o wyrazach nieujemnych. Wtedy
o wyrazach nieujemnych. Wtedy
A) 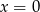 B)
B) 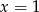 C)
C) 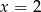 D)
D) 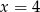
Dany jest ciąg geometryczny 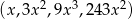 o wyrazach dodatnich. Wtedy
o wyrazach dodatnich. Wtedy
A) 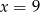 B)
B) 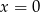 C)
C) 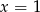 D)
D) 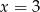
Dany jest ciąg geometryczny 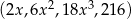 o wyrazach dodatnich. Wtedy
o wyrazach dodatnich. Wtedy
A) 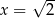 B)
B) 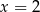 C)
C) 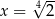 D)
D) 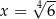
Prosta o równaniu 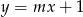 jest prostopadła do prostej o równaniu
jest prostopadła do prostej o równaniu 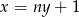 . Stąd wynika, że
. Stąd wynika, że
A) 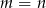 B)
B) 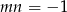 C)
C) 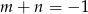 D)
D) 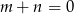
Prosta o równaniu 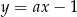 jest prostopadła do prostej o równaniu
jest prostopadła do prostej o równaniu 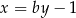 . Stąd wynika, że
. Stąd wynika, że
A) 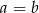 B)
B) 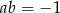 C)
C) 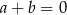 D)
D) 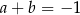
Przekątne deltoidu są zawarte w prostych o równaniach 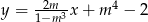 oraz
oraz 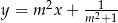 . Zatem
. Zatem
A) 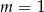 B)
B) 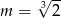 C)
C) 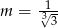 D)
D) 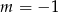
Na loterii jest 10 losów, z których 4 są wygrywające. Kupujemy jeden los. Prawdopodobieństwo zdarzenia, że nie wygramy nagrody, jest równe
A)  B)
B)  C)
C)  D)
D) 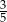
W pudełku jest 50 kuponów, wśród których jest 15 kuponów przegrywających, a pozostałe kupony są wygrywające. Z tego pudełka w sposób losowy wyciągamy jeden kupon. Prawdopodobieństwo zdarzenia polegającego na tym, że wyciągniemy kupon wygrywający, jest równe
A) 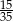 B)
B) 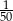 C)
C) 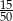 D)
D) 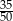
Na loterii jest 12 losów, z których 8 jest przegrywających. Kupujemy jeden los. Prawdopodobieństwo zdarzenia, że wygramy nagrodę jest równe
A) 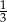 B)
B) 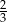 C)
C) 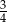 D)
D) 
Na loterii jest 20 losów, z których 8 jest wygrywających. Kupujemy jeden los. Prawdopodobieństwo zdarzenia, że nie wygramy nagrody jest równe
A) 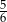 B)
B) 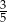 C)
C) 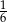 D)
D) 
Na loterii jest 14 losów, z których 6 jest wygrywających. Kupujemy jeden los. Prawdopodobieństwo zdarzenia, że nie wygramy nagrody jest równe
A)  B)
B)  C)
C) 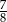 D)
D) 
Liczba  jest liczbą naturalną większą od 1 i
jest liczbą naturalną większą od 1 i 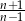 jest liczbą naturalną. Z tego wynika, że liczbą naturalną jest również liczba
jest liczbą naturalną. Z tego wynika, że liczbą naturalną jest również liczba
A) 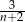 B)
B) 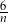 C)
C) 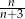 D)
D) 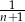
Liczba  jest liczbą naturalną większą od 2 i
jest liczbą naturalną większą od 2 i 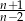 jest liczbą naturalną. Z tego wynika, że liczbą naturalną jest również liczba
jest liczbą naturalną. Z tego wynika, że liczbą naturalną jest również liczba
A) 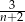 B)
B) 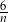 C)
C) 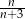 D)
D) 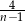
Liczba  jest liczbą naturalną większą od 2 i
jest liczbą naturalną większą od 2 i 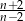 jest liczbą naturalną. Z tego wynika, że liczbą naturalną jest również liczba
jest liczbą naturalną. Z tego wynika, że liczbą naturalną jest również liczba
A) 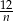 B)
B) 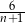 C)
C) 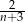 D)
D) 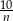
Liczba  jest liczbą naturalną większą od 1 i
jest liczbą naturalną większą od 1 i 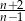 jest liczbą naturalną. Z tego wynika, że liczbą naturalną jest również liczba
jest liczbą naturalną. Z tego wynika, że liczbą naturalną jest również liczba
A) 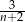 B)
B) 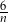 C)
C) 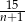 D)
D) 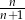
Liczba 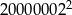 jest równa
jest równa
A) 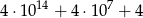 B)
B) 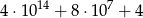 C) 40 000 004 D)
C) 40 000 004 D) 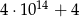
Liczba 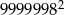 jest równa
jest równa
A) 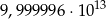 B)
B) 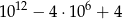 C)
C) 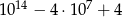 D)
D) 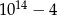
Okręgi o promieniach 3 i 4 są styczne zewnętrznie. Prosta 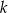 jest styczna do okręgu o promieniu 3 w punkcie
jest styczna do okręgu o promieniu 3 w punkcie 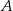 i jest styczna do okręgu o promieniu 4 w punkcie
i jest styczna do okręgu o promieniu 4 w punkcie 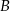 (zobacz rysunek).
(zobacz rysunek).
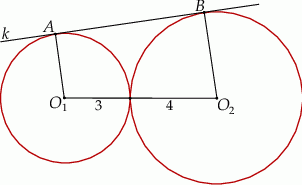
Długość odcinka 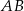 jest równa
jest równa
A) 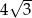 B) 7 C) 6 D)
B) 7 C) 6 D) 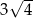
Dane są liczby 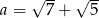 oraz
oraz 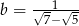 . Zatem
. Zatem
A) 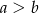 B)
B) 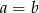 C)
C) 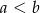 D)
D) 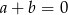
Dane są liczby 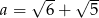 oraz
oraz 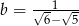 . Zatem
. Zatem
A) 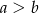 B)
B) 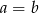 C)
C) 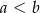 D)
D) 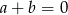
Dane są liczby 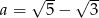 oraz
oraz 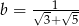 . Zatem
. Zatem
A) 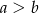 B)
B) 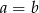 C)
C) 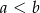 D)
D) 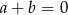
Firma przeprowadziła badania rynkowe dotyczące wpływu zmiany ceny 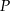 swojego produktu na liczbę
swojego produktu na liczbę 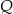 kupujących ten produkt. Z badań wynika, że każdorazowe zwiększenie ceny o 1 jednostkę powoduje spadek liczby kupujących o 3 jednostki. Ponadto przy cenie równej 5 jednostek liczba kupujących jest równa 12 jednostek. Funkcja, która opisuje zależność liczby kupujących ten produkt od jego ceny, ma wzór
kupujących ten produkt. Z badań wynika, że każdorazowe zwiększenie ceny o 1 jednostkę powoduje spadek liczby kupujących o 3 jednostki. Ponadto przy cenie równej 5 jednostek liczba kupujących jest równa 12 jednostek. Funkcja, która opisuje zależność liczby kupujących ten produkt od jego ceny, ma wzór
A) 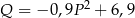 B)
B) 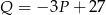
C) 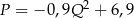 D)
D) 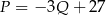
Firma przeprowadziła badania dotyczące wpływu zmiany dziennego kosztu produkcji 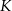 swojego produktu w zależności od liczby
swojego produktu w zależności od liczby 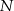 wyprodukowanych jednego dnia sztuk produktu. Z badań wynika, że każdorazowe zwiększenie dziennej produkcji o 10 sztuk produktu, powoduje wzrost dziennego kosztu produkcji o 15 jednostek. Ponadto, przy produkcji na poziomie 10 sztuk dziennie dzienny koszt produkcji jest równy 60 jednostek. Funkcja, która opisuje zależność dziennego kosztu produkcji przedmiotu od dziennej liczby produkowanych sztuk, ma wzór
wyprodukowanych jednego dnia sztuk produktu. Z badań wynika, że każdorazowe zwiększenie dziennej produkcji o 10 sztuk produktu, powoduje wzrost dziennego kosztu produkcji o 15 jednostek. Ponadto, przy produkcji na poziomie 10 sztuk dziennie dzienny koszt produkcji jest równy 60 jednostek. Funkcja, która opisuje zależność dziennego kosztu produkcji przedmiotu od dziennej liczby produkowanych sztuk, ma wzór
A) 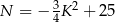 B)
B) 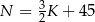
C) 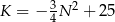 D)
D) 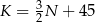
Punkt 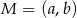 jest środkiem odcinka o końcach
jest środkiem odcinka o końcach 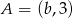 i
i 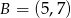 . Wówczas
. Wówczas
A) 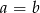 B)
B) 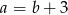 C)
C) 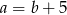 D)
D) 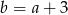
Punkt 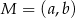 jest środkiem odcinka o końcach
jest środkiem odcinka o końcach 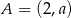 i
i 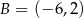 . Wówczas
. Wówczas
A) 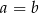 B)
B) 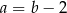 C)
C) 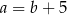 D)
D) 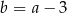
W układzie współrzędnych dane są punkty 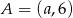 oraz
oraz 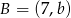 . Środkiem odcinka
. Środkiem odcinka 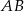 jest punkt
jest punkt 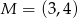 . Wynika stąd, że
. Wynika stąd, że
A) 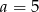 i
i 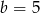 B)
B) 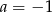 i
i 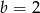 C)
C) 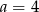 i
i 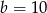 D)
D) 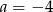 i
i 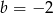
Jeżeli 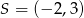 jest środkiem odcinka o końcach
jest środkiem odcinka o końcach 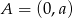 i
i 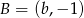 , to
, to
A) 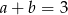 B)
B) 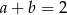 C)
C) 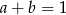 D)
D) 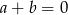
Środkiem odcinka o końcach 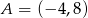 i
i 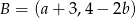 jest początek prostokątnego układu współrzędnych. Wówczas
jest początek prostokątnego układu współrzędnych. Wówczas
A) 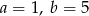 B)
B) 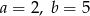 C)
C) 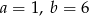 D)
D) 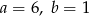
W układzie współrzędnych dane są punkty 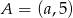 oraz
oraz 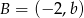 . Środkiem odcinka
. Środkiem odcinka 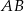 jest punkt
jest punkt 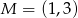 . Wynika stąd, że
. Wynika stąd, że
A) 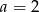 i
i 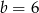 B)
B) 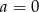 i
i 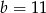 C)
C) 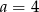 i
i 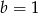 D)
D) 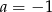 i
i 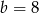
W układzie współrzędnych dane są punkty 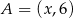 ,
, 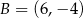 oraz
oraz 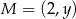 . Jeżeli punkt
. Jeżeli punkt 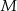 jest środkiem odcinka
jest środkiem odcinka 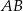 , to
, to
A) 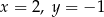 B)
B) 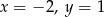 C)
C) 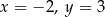 D)
D) 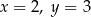
Punkt 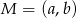 jest środkiem odcinka o końcach
jest środkiem odcinka o końcach 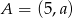 i
i 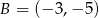 . Wówczas
. Wówczas
A) 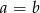 B)
B) 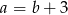 C)
C) 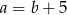 D)
D) 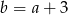
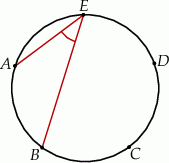
Punkty 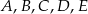 dzielą okrąg na 5 równych łuków. Miara zaznaczonego na rysunku kąta wpisanego
dzielą okrąg na 5 równych łuków. Miara zaznaczonego na rysunku kąta wpisanego 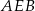 jest równa
jest równa
A) 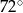 B)
B) 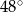 C)
C) 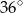 D)
D) 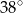
Punkty 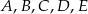 leżące na okręgu o środku
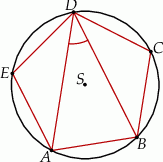
leżące na okręgu o środku 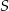 są wierzchołkami pięciokąta foremnego. Miara zaznaczonego na rysunku kąta wpisanego
są wierzchołkami pięciokąta foremnego. Miara zaznaczonego na rysunku kąta wpisanego 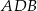 jest równa
jest równa
A) 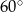 B)
B) 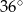 C)
C) 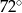 D)
D) 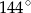
Punkty 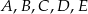 okręgu są wierzchołkami pięciokąta foremnego. Miara zaznaczonego na rysunku kąta wpisanego
okręgu są wierzchołkami pięciokąta foremnego. Miara zaznaczonego na rysunku kąta wpisanego 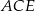 jest równa
jest równa
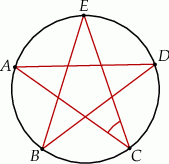
A) 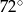 B)
B) 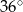 C)
C) 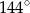 D)
D) 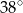
W trójkącie równoramiennym 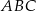 dane są
dane są 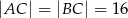 oraz
oraz 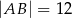 . Odcinek
. Odcinek 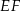 jest równoległy do podstawy
jest równoległy do podstawy 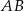 oraz
oraz 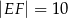 . Długość odcinka
. Długość odcinka 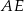 jest równa
jest równa
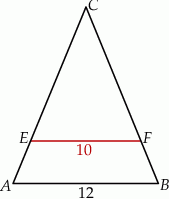
A) 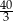 B)
B)  C)
C) 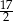 D)
D) 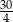
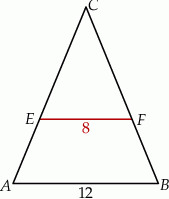
W trójkącie równoramiennym 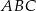 dane są
dane są 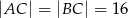 oraz
oraz 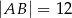 . Odcinek
. Odcinek 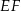 jest równoległy do podstawy
jest równoległy do podstawy 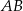 oraz
oraz 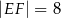 . Długość odcinka
. Długość odcinka 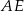 jest równa
jest równa
A) 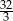 B)
B)  C)
C) 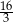 D)
D) 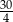
Dana jest funkcja kwadratowa 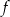 , której fragment wykresu przedstawiono na rysunku poniżej. Wykresem funkcji
, której fragment wykresu przedstawiono na rysunku poniżej. Wykresem funkcji 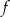 jest parabola, której punkty przecięcia z osiami układu współrzędnych mają współrzędne całkowite.
jest parabola, której punkty przecięcia z osiami układu współrzędnych mają współrzędne całkowite.
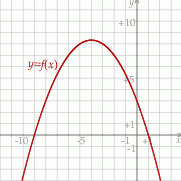
Funkcja 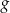 jest określona za pomocą funkcji
jest określona za pomocą funkcji 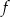 następująco:
następująco: 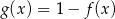 . Wykres funkcji
. Wykres funkcji 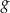 przedstawiono na rysunku
przedstawiono na rysunku