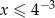Funkcja 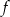 przyporządkowuje każdej liczbie naturalnej większej od 1 liczbę liczb pierwszych mniejszych od
przyporządkowuje każdej liczbie naturalnej większej od 1 liczbę liczb pierwszych mniejszych od  . Liczba
. Liczba 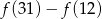 jest równa
jest równa
A) 5 B) 6 C) 4 D) 10
/Szkoła średnia/Zadania testowe
Dany jest ciąg geometryczny 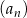 o wszystkich wyrazach niezerowych i pierwszym wyrazie
o wszystkich wyrazach niezerowych i pierwszym wyrazie 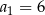 . Jeżeli
. Jeżeli 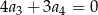 , to wzorem ogólnym ciągu
, to wzorem ogólnym ciągu 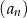 jest
jest
A) 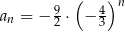 B)
B) 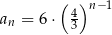 C)
C) 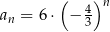 D)
D) 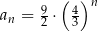
Dany jest ciąg geometryczny 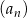 o wszystkich wyrazach niezerowych i pierwszym wyrazie
o wszystkich wyrazach niezerowych i pierwszym wyrazie 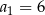 . Jeżeli
. Jeżeli 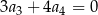 , to wzorem ogólnym ciągu
, to wzorem ogólnym ciągu 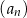 jest
jest
A) 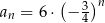 B)
B) 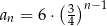 C)
C) 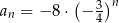 D)
D) 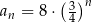
Funkcja 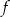 jest określona wzorem
jest określona wzorem 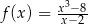 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej 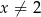 . Wartość pochodnej tej funkcji dla argumentu
. Wartość pochodnej tej funkcji dla argumentu 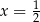 jest równa
jest równa
A) 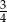 B)
B) 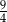 C) 3 D)
C) 3 D) 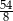
W romb o boku 2 i kącie 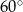 wpisano okrąg. Promień tego okręgu jest równy
wpisano okrąg. Promień tego okręgu jest równy
A) 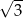 B)
B) 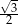 C)
C) 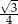 D)
D) 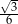
Przekrój osiowy walca jest prostokątem, w którym przekątne przecinają się pod kątem 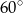 . Wysokość walca jest równa
. Wysokość walca jest równa 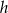 i jest krótsza od średnicy podstawy. Promień podstawy tego walca jest równy
i jest krótsza od średnicy podstawy. Promień podstawy tego walca jest równy
A) 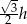 B)
B) 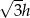 C)
C) 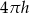 D)
D) 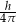
Przekrój osiowy walca jest prostokątem, w którym przekątne przecinają się pod kątem 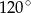 . Wysokość walca jest równa
. Wysokość walca jest równa 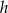 i jest krótsza od średnicy podstawy. Promień podstawy tego walca jest równy
i jest krótsza od średnicy podstawy. Promień podstawy tego walca jest równy
A) 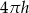 B)
B) 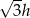 C)
C) 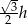 D)
D) 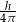
Pole powierzchni jednej ściany sześcianu jest równe 4. Objętość tego sześcianu jest równa
A) 6 B) 8 C) 24 D) 64
Pole powierzchni jednej ściany sześcianu jest równe 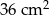 . Objętość tego sześcianu jest równa
. Objętość tego sześcianu jest równa
A) 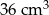 B)
B) 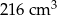 C)
C) 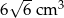 D)
D) 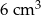
Pole powierzchni jednej ściany sześcianu jest równe 9. Objętość tego sześcianu jest równa
A) 9 B) 27 C) 54 D) 81
Wyrażenie 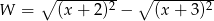 dla
dla 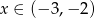 przyjmuje postać
przyjmuje postać
A) 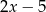 B)
B) 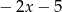 C) -1 D)
C) -1 D) 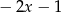
Wyrażenie 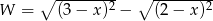 dla
dla 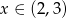 przyjmuje postać
przyjmuje postać
A) 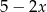 B) 5 C) -1 D)
B) 5 C) -1 D) 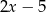
Wyrażenie 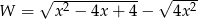 dla
dla 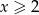 przyjmuje postać
przyjmuje postać
A) 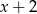 B)
B) 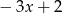 C)
C) 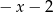 D)
D) 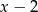
Dla każdego kąta  wyrażenie
wyrażenie 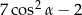 jest równe
jest równe
A) 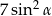 B)
B) 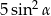
C)  D)
D) 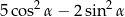
Liczba 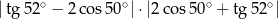 jest równa
jest równa
A) 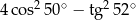 B)
B) 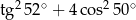
C) 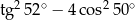 D)
D) 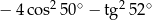
Wiadomo, że  jest kątem ostrym i
jest kątem ostrym i 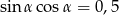 . Wynika stąd, że wartość wyrażenia
. Wynika stąd, że wartość wyrażenia 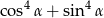 jest równa
jest równa
A) 1 B) 0,5 C) 0,25 D) 0,75
Wiadomo, że  jest kątem ostrym i
jest kątem ostrym i 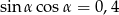 . Wynika stąd, że wartość wyrażenia
. Wynika stąd, że wartość wyrażenia 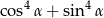 jest równa
jest równa
A) 0,68 B) 0,84 C) 0,32 D) 0,16
Wiadomo, że  jest kątem ostrym i
jest kątem ostrym i 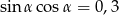 . Wynika stąd, że wartość wyrażenia
. Wynika stąd, że wartość wyrażenia 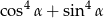 jest równa
jest równa
A) 0,18 B) 0,91 C) 0,82 D) 0,75
Ramię końcowe kąta 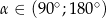 zawiera się w prostej
zawiera się w prostej 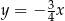 . Zatem
. Zatem
A) 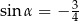 B)
B) 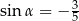 C)
C) 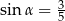 D)
D) 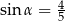
Punkty 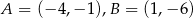 i
i 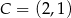 są trzema kolejnymi wierzchołkami rombu
są trzema kolejnymi wierzchołkami rombu 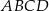 . Pole tego rombu jest równe
. Pole tego rombu jest równe
A) 40 B) 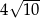 C) 80 D) 20
C) 80 D) 20
Rozwiązaniem równania 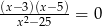 jest liczba:
jest liczba:
A) 3 B) -5 C) 5 D) 0
Rozwiązaniem równania 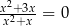 jest liczba
jest liczba
A) 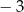 B) 0 C) 3 D) 9
B) 0 C) 3 D) 9
Rozwiązaniem równania 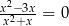 jest liczba
jest liczba
A) 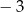 B) 0 C) 3 D) 9
B) 0 C) 3 D) 9
W grupie 50 kobiet i 50 mężczyzn przeprowadzono ankietę, w której zadano pytanie o liczbę książek przeczytanych w ostatnim roku. Wyniki ankiety zebrano w poniższej tabeli.
| Liczba książek | 0 | 1 | 2 | 3 | 4 | 5 |
| Liczba osób | 23 | 14 | 28 | 17 | 11 | 7 |
W trakcie analizy tych danych zauważono, że kobiety przeczytały średnio o jedną książkę więcej niż mężczyźni. Średnia liczba przeczytanych książek przez jednego ankietowanego mężczyznę jest równa
A) 1,5 B) 1 C) 2 D) 2,5
W grupie 50 kobiet i 50 mężczyzn przeprowadzono ankietę, w której zadano pytanie o liczbę książek przeczytanych w ostatnim roku. Wyniki ankiety zebrano w poniższej tabeli.
| Liczba książek | 0 | 1 | 2 | 3 | 4 | 5 |
| Liczba osób | 19 | 21 | 24 | 21 | 7 | 8 |
W trakcie analizy tych danych zauważono, że kobiety przeczytały średnio o dwie książki więcej niż mężczyźni. Średnia liczba przeczytanych książek przez jednego ankietowanego mężczyznę jest równa
A) 1,5 B) 1 C) 2 D) 2,5
W grupie 50 kobiet i 50 mężczyzn przeprowadzono ankietę, w której zadano pytanie o liczbę książek przeczytanych w ostatnim roku. Wyniki ankiety zebrano w poniższej tabeli.
| Liczba książek | 0 | 1 | 2 | 3 | 4 | 5 |
| Liczba osób | 23 | 14 | 28 | 17 | 11 | 7 |
W trakcie analizy tych danych zauważono, że kobiety przeczytały średnio o jedną książkę więcej niż mężczyźni. Średnia liczba przeczytanych książek przez jedną ankietowaną kobietę jest równa
A) 1,5 B) 1 C) 2 D) 2,5
Punkty 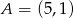 oraz
oraz 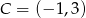 są przeciwległymi wierzchołkami kwadratu
są przeciwległymi wierzchołkami kwadratu 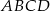 . Bok tego kwadratu ma długość:
. Bok tego kwadratu ma długość:
A) 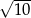 B)
B) 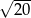 C)
C) 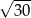 D)
D) 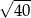
Punkty 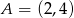 oraz
oraz 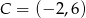 są przeciwległymi wierzchołkami kwadratu
są przeciwległymi wierzchołkami kwadratu 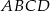 . Bok tego kwadratu ma długość:
. Bok tego kwadratu ma długość:
A) 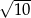 B)
B) 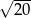 C)
C) 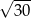 D)
D) 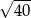
Punkty 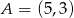 oraz
oraz 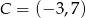 są przeciwległymi wierzchołkami kwadratu
są przeciwległymi wierzchołkami kwadratu 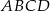 . Bok tego kwadratu ma długość:
. Bok tego kwadratu ma długość:
A) 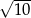 B)
B) 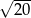 C)
C) 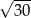 D)
D) 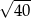
Poniżej zamieszczono fragment tabeli wartości funkcji liniowej
 | 1 | 2 | 4 |
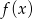 | 4 | 1 |
W pustym miejscu w tabeli powinna znajdować się liczba:
A) 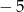 B) 5 C)
B) 5 C) 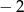 D) 2
D) 2
Pary liczb 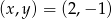 i
i 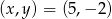 należą do zbioru rozwiązań układu równań
należą do zbioru rozwiązań układu równań
A) 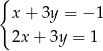 B)
B) 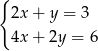 C)
C) 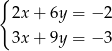 D)
D) 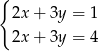
Pary liczb 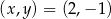 i
i 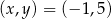 należą do zbioru rozwiązań układu równań
należą do zbioru rozwiązań układu równań
A) 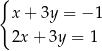 B)
B) 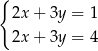 C)
C) 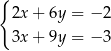 D)
D) 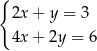
Która z poniższych równości jest fałszywa?
A) 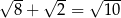 B)
B) 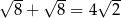
C) 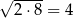 D)
D) 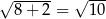
Która z poniższych równości jest prawdziwa?
A) 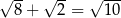 B)
B) 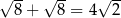
C) 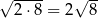 D)
D) 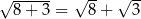
Która z poniższych równości jest fałszywa?
A) 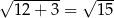 B)
B) 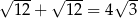
C) 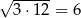 D)
D) 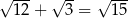
Punkt 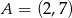 jest wierzchołkiem kwadratu
jest wierzchołkiem kwadratu 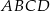 , a punkt
, a punkt 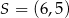 jest środkiem okręgu opisanego na tym kwadracie. Bok tego kwadratu ma długość
jest środkiem okręgu opisanego na tym kwadracie. Bok tego kwadratu ma długość
A) 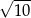 B)
B) 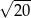 C)
C) 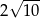 D)
D) 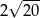
Punkt 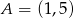 jest wierzchołkiem kwadratu
jest wierzchołkiem kwadratu 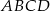 , a punkt
, a punkt 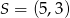 jest środkiem okręgu opisanego na tym kwadracie. Bok tego kwadratu ma długość
jest środkiem okręgu opisanego na tym kwadracie. Bok tego kwadratu ma długość
A) 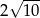 B)
B) 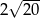 C)
C) 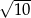 D)
D) 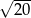
Wiadomo, że 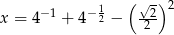 . Zatem
. Zatem
A) 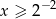 B)
B) 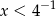 C)
C) 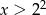 D)
D) 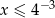
Wiadomo, że 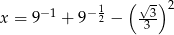 . Zatem
. Zatem
A) 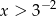 B)
B) 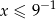 C)
C) 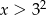 D)
D) 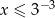
Wiadomo, że 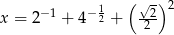 . Zatem
. Zatem
A) 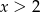 B)
B) 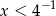 C)
C) 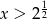 D)
D)