Na rysunku przedstawiono fragment prostej o równaniu 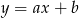 .
.
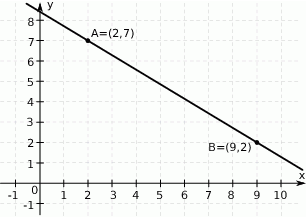
Punkt 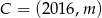 leży na tej prostej. Zatem
leży na tej prostej. Zatem
A) 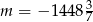 B)
B) 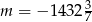 C)
C) 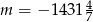 D)
D) 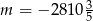
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Na rysunku przedstawiono fragment prostej o równaniu 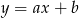 .
.

Punkt 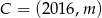 leży na tej prostej. Zatem
leży na tej prostej. Zatem
A) 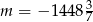 B)
B) 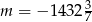 C)
C) 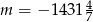 D)
D) 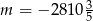
Do naczynia o pojemności 2,5 l i wlano 0,75 l wody. Jaki procent tego naczynia stanowi objętość wody?
A) 3% B) 60% C) 3,(3)% D) 30%
Pierwszy wyraz ciągu arytmetycznego jest równy 5, a różnica tego ciągu jest równa 3. Suma 100 początkowych wyrazów tego ciągu o numerach parzystych jest równa
A) 15100 B) 30500 C) 30200 D) 61000
W ciągu geometrycznym 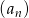 dane są
dane są 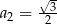 i
i 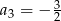 . Wtedy wyraz
. Wtedy wyraz 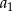 jest równy
jest równy
A) 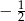 B)
B) 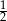 C)
C) 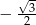 D)
D) 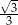
W ciągu geometrycznym 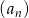 dane są
dane są 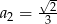 i
i 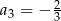 . Wtedy wyraz
. Wtedy wyraz 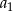 jest równy
jest równy
A) 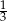 B)
B) 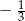 C)
C) 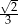 D)
D) 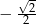
Jeżeli 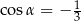 i
i  jest kątem rozwartym, to wartość
jest kątem rozwartym, to wartość 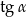 jest równa
jest równa
A) 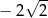 B)
B) 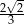 C)
C) 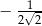 D)
D) 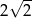
Prosta 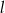 jest styczna do okręgu o środku
jest styczna do okręgu o środku 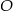 w punkcie
w punkcie 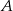 ,
, 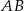 jest cięciwą okręgu,
jest cięciwą okręgu, 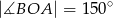 . Wówczas kąt ostry
. Wówczas kąt ostry  między cięciwą
między cięciwą 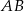 , a prostą
, a prostą 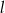 jest równy
jest równy
A) 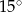 B)
B) 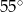 C)
C) 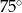 D)
D) 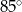
W okręgu o środku w punkcie 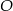 poprowadzono cięciwę
poprowadzono cięciwę 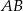 . Trójkąt
. Trójkąt 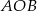 jest prostokątny. Miara kąta, jaki tworzy cięciwa
jest prostokątny. Miara kąta, jaki tworzy cięciwa 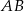 ze styczną do okręgu poprowadzoną w punkcie
ze styczną do okręgu poprowadzoną w punkcie 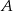 , jest równa
, jest równa
A) 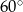 B)
B) 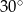 C)
C) 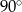 D)
D) 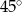
Liczba przekątnych wielokąta wypukłego jest 4 razy większa od liczby jego boków. Wynika stąd, że liczba boków tego wielokąta jest równa
A) 8 B) 9 C) 10 D) 11
Liczba przekątnych wielokąta wypukłego jest 6 razy większa od liczby jego boków. Wynika stąd, że liczba boków tego wielokąta jest równa
A) 15 B) 14 C) 13 D) 12
Liczba przekątnych wielokąta wypukłego jest 5 razy większa od liczby jego boków. Wynika stąd, że liczba boków tego wielokąta jest równa
A) 10 B) 11 C) 13 D) 14
W którym wielokącie liczba przekątnych jest dwa razy większa od liczby boków?
A) w pięciokącie B) w sześciokącie C) w siedmiokącie D) w ośmiokącie
Która z poniższych równości jest prawdziwa dla każdej liczby rzeczywistej  ?
?
A) 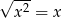 B)
B) 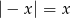 C)
C) 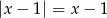 D)
D) 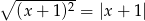
Która z poniższych równości jest prawdziwa dla każdej liczby rzeczywistej  ?
?
A) 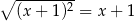 B)
B) 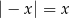 C)
C) 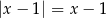 D)
D) 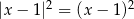
Wartość wyrażenia 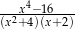 dla
dla 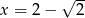 jest równa
jest równa
A) 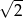 B)
B) 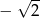 C) 2 D) -2
C) 2 D) -2
Wartość wyrażenia 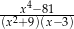 dla
dla 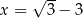 jest równa
jest równa
A) 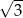 B)
B) 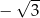 C) 3 D)
C) 3 D) 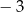
W pudełku znajdują się płytki z literami i cyframi. Na każdej płytce jest wydrukowana albo jedna wielka litera, albo jedna mała litera, albo jedna cyfra. Płytek z wielkimi literami jest o 25% mniej niż płytek z cyframi, a płytek z małymi literami jest o 40% więcej niż płytek z wielkimi literami. Losujemy jedną płytkę. Prawdopodobieństwo wylosowania płytki z cyfrą jest równe
A) 0,85 B) 0,1 C) 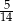 D)
D) 
Po skróceniu wyrażenia 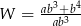 otrzymamy
otrzymamy
A) 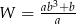 B)
B) 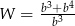 C)
C) 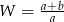 D)
D) 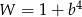
Po skróceniu wyrażenia 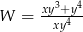 otrzymamy
otrzymamy
A) 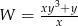 B)
B) 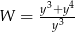 C)
C) 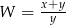 D)
D) 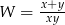
Po skróceniu wyrażenia 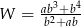 otrzymamy
otrzymamy
A) 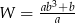 B)
B) 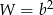 C)
C) 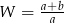 D)
D) 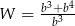
Jednym z rozwiązań równania 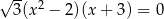 jest liczba
jest liczba
A) 3 B) 2 C) 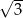 D)
D) 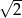
Jednym z rozwiązań równania 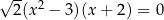 jest liczba
jest liczba
A) 3 B) 2 C) 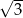 D)
D) 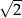
Odcinek 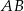 jest średnicą okręgu o środku
jest średnicą okręgu o środku 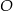 .
.
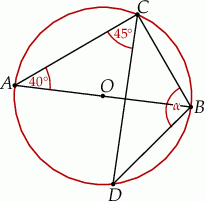
Miara kąta 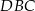 oznaczonego na rysunku literą
oznaczonego na rysunku literą  jest równa
jest równa
A) 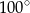 B)
B) 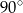 C)
C) 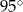 D)
D) 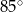
Punkty 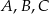 i
i 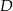 leżą na okręgu o środku
leżą na okręgu o środku 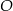 . Punkt
. Punkt 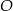 leży na odcinku
leży na odcinku 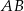 oraz
oraz 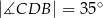 ,
, 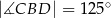 .
.
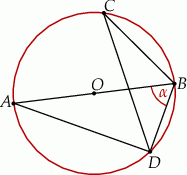
Miara kąta 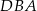 oznaczonego na rysunku literą
oznaczonego na rysunku literą  jest równa
jest równa
A) 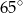 B)
B) 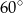 C)
C) 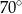 D)
D) 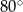
Odcinek 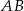 jest średnicą okręgu o środku
jest średnicą okręgu o środku 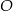 .
.
Miara kąta 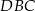 oznaczonego na rysunku literą
oznaczonego na rysunku literą  jest równa
jest równa
A) 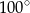 B)
B) 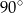 C)
C) 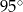 D)
D) 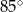
Funkcja kwadratowa 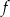 jest określona wzorem
jest określona wzorem 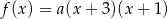 . Na rysunku przedstawiono fragment paraboli będącej wykresem tej funkcji. Jednym z punktów tej paraboli jest punkt
. Na rysunku przedstawiono fragment paraboli będącej wykresem tej funkcji. Jednym z punktów tej paraboli jest punkt 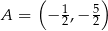 .
.
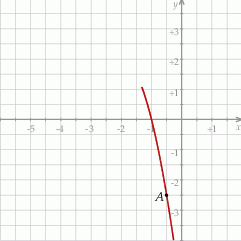
Osią symetrii paraboli będącej wykresem funkcji 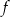 jest prosta o równaniu
jest prosta o równaniu
A) 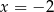 B)
B) 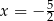 C)
C) 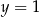 D)
D) 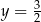
Do wykresu funkcji 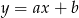 należą punkty
należą punkty 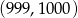 oraz
oraz 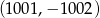 . Wówczas
. Wówczas
A) 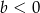 B)
B) 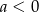 C)
C) 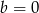 D)
D) 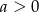
Do wykresu funkcji 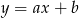 należą punkty
należą punkty 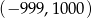 oraz
oraz 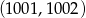 . Wówczas
. Wówczas
A) 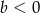 B)
B) 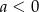 C)
C) 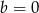 D)
D) 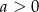
Rozwiązaniem równania 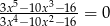 jest liczba
jest liczba
A) 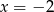 B)
B) 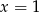 C)
C) 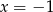 D)
D) 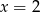
Wiadomo, że 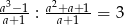 . Zatem
. Zatem 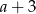 jest równe
jest równe
A) 7 B) 1 C) -1 D) 5
Wiadomo, że 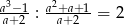 . Zatem
. Zatem 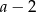 jest równe
jest równe
A) 7 B) 1 C) -1 D) 5
Wiadomo, że 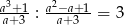 . Zatem
. Zatem 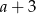 jest równe
jest równe
A) 7 B) 1 C) -1 D) 5
Punkty 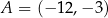 ,
, 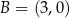 i
i 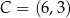 są kolejnymi wierzchołkami równoległoboku
są kolejnymi wierzchołkami równoległoboku 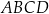 . Wierzchołek
. Wierzchołek 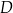 tego równoległoboku ma współrzędne
tego równoległoboku ma współrzędne
A) 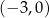 B)
B) 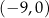 C)
C) 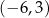 D)
D) 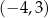
Dany jest okrąg o środku 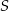 . Punkty
. Punkty 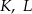 i
i 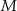 leżą na tym okręgu. Na łuku
leżą na tym okręgu. Na łuku 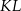 tego okręgu są oparte kąty
tego okręgu są oparte kąty 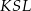 i
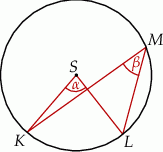
i 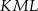 (zobacz rysunek), których miary
(zobacz rysunek), których miary  i
i 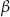 spełniają warunek
spełniają warunek 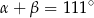 . Wynika stąd, że
. Wynika stąd, że
A) 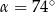 B)
B) 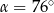 C)
C) 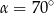 D)
D) 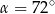
Dany jest okrąg o środku 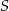 . Punkty
. Punkty 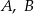 i
i 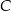 leżą na tym okręgu. Na łuku
leżą na tym okręgu. Na łuku 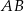 tego okręgu są oparte kąty
tego okręgu są oparte kąty 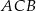 i
i 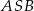 (zobacz rysunek), których miary
(zobacz rysunek), których miary  i
i 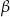 spełniają warunek
spełniają warunek 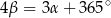 . Wynika stąd, że
. Wynika stąd, że
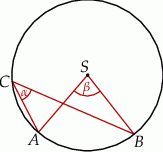
A) 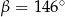 B)
B) 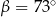 C)
C) 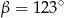 D)
D) 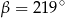
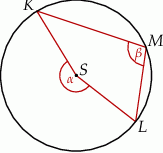
Dany jest okrąg o środku 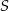 . Punkty
. Punkty 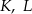 i
i 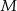 leżą na tym okręgu. Na łuku
leżą na tym okręgu. Na łuku 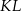 tego okręgu są oparte kąty
tego okręgu są oparte kąty 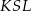 i
i 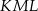 (zobacz rysunek), których miary
(zobacz rysunek), których miary  i
i 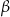 spełniają warunek
spełniają warunek 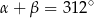 . Wynika stąd, że
. Wynika stąd, że
A) 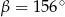 B)
B) 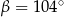 C)
C) 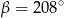 D)
D) 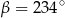
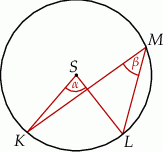
Dany jest okrąg o środku 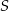 . Punkty
. Punkty 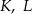 i
i 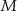 leżą na tym okręgu. Na łuku
leżą na tym okręgu. Na łuku 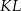 tego okręgu są oparte kąty
tego okręgu są oparte kąty 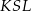 i
i 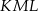 (zobacz rysunek), których miary
(zobacz rysunek), których miary  i
i 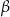 spełniają warunek
spełniają warunek 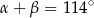 . Wynika stąd, że
. Wynika stąd, że
A) 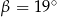 B)
B) 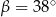 C)
C) 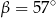 D)
D) 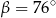
Jednym z pierwiastków równania 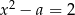 , gdzie
, gdzie  jest liczbą dodatnią, jest liczba
jest liczbą dodatnią, jest liczba 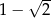 . Zatem drugim pierwiastkiem tego równania jest liczba:
. Zatem drugim pierwiastkiem tego równania jest liczba:
A) 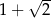 B)
B) 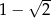 C)
C) 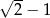 D) 0
D) 0
