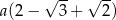Wysokość trójkąta równobocznego jest o 2 krótsza od boku tego trójkąta. Bok trójkąta ma długość
A) 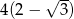 B)
B) 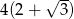 C)
C) 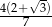 D)
D) 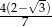
/Szkoła średnia/Zadania testowe
Wysokość trójkąta równobocznego jest o 3 krótsza od boku tego trójkąta. Bok trójkąta jest ma długość
A) 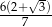 B)
B) 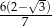 C)
C) 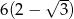 D)
D) 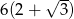
Wysokość trójkąta równobocznego jest o 4 krótsza od boku tego trójkąta. Bok trójkąta ma długość
A) 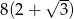 B)
B) 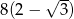 C)
C) 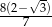 D)
D) 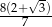
Współczynnik kierunkowy prostej prostopadłej do prostej określonej wzorem 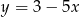 jest równy
jest równy
A) 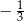 B) 3 C) -5 D)
B) 3 C) -5 D) 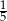
Współczynnik kierunkowy prostej prostopadłej do prostej określonej wzorem 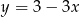 jest równy
jest równy
A) 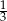 B) 3 C) -3 D)
B) 3 C) -3 D) 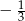
Współczynnik kierunkowy prostej prostopadłej do prostej określonej wzorem 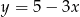 jest równy
jest równy
A) 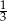 B) -3 C) 5 D)
B) -3 C) 5 D) 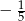
Prosta 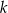 ma równanie
ma równanie 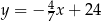 . Współczynnik kierunkowy prostej prostopadłej do prostej
. Współczynnik kierunkowy prostej prostopadłej do prostej 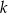 jest równy
jest równy
A)  B)
B) 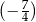 C)
C) 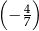 D)
D) 
Współczynnik kierunkowy prostej prostopadłej do prostej określonej wzorem 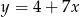 jest równy
jest równy
A) 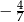 B)
B) 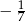 C) 7 D)
C) 7 D) 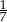
Jeśli wykres funkcji kwadratowej 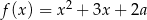 jest styczny do prostej
jest styczny do prostej 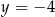 , to
, to
A) 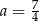 B)
B) 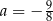 C)
C) 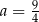 D)
D) 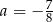
Jeśli wykres funkcji kwadratowej 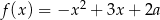 jest styczny do prostej
jest styczny do prostej 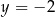 , to
, to
A) 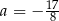 B)
B) 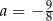 C)
C) 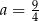 D)
D) 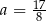
Ze zbioru dwucyfrowych liczb naturalnych wybieramy losowo jedną liczbę. Prawdopodobieństwo otrzymania liczby podzielnej przez 30 jest równe
A) 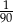 B)
B) 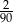 C)
C) 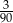 D)
D) 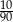
Ze zbioru dwucyfrowych liczb naturalnych wybieramy losowo jedną liczbę. Prawdopodobieństwo otrzymania liczby podzielnej przez 15 jest równe
A) 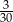 B)
B) 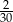 C)
C) 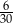 D)
D) 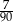
Ze zbioru liczb naturalnych dwucyfrowych nie mniejszych od 50 losujemy jedną liczbę. Jakie jest prawdopodobieństwo, że wylosowana liczba będzie podzielna przez 5?
A) 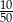 B)
B) 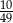 C)
C) 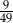 D)
D) 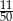
Ze zbioru liczb naturalnych dwucyfrowych nie mniejszych od 40 losujemy jedną liczbę. Jakie jest prawdopodobieństwo, że wylosowana liczba będzie podzielna przez 5?
A) 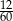 B)
B) 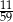 C)
C) 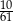 D)
D) 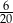
Wartość wyrażenia 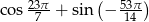 jest równa
jest równa
A) 0 B) 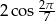 C)
C) 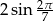 D)
D) 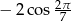
Dla każdych liczb rzeczywistych  i
i 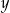 wyrażenie
wyrażenie 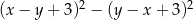 jest równe
jest równe
A) 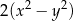 B)
B) 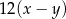 C)
C) 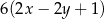 D) 9
D) 9
Wielomian 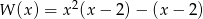 można zapisać w postaci
można zapisać w postaci
A) 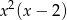 B)
B) 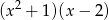 C)
C) 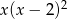 D)
D) 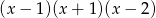
Wielomian 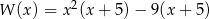 można przedstawić w postaci
można przedstawić w postaci
A) 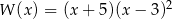 B)
B) 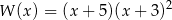
C) 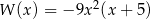 D)
D) 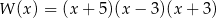
Wielomian 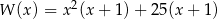 można przedstawić w postaci
można przedstawić w postaci
A) 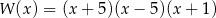 B)
B) 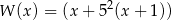
C) 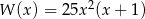 D)
D) 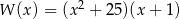
Wielomian 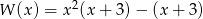 można zapisać w postaci
można zapisać w postaci
A) 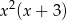 B)
B) 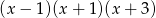 C)
C) 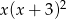 D)
D) 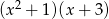
Trapez 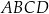 podzielono przekątną
podzielono przekątną 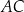 na dwa trójkąty. Punkty
na dwa trójkąty. Punkty 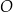 i
i 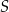 są środkami okręgów wpisanych w trójkąty
są środkami okręgów wpisanych w trójkąty 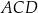 i
i 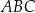 , a odcinek
, a odcinek 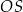 przecina przekątną
przecina przekątną 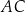 w punkcie
w punkcie 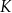 (zobacz rysunek). Stosunek długości okręgów o środkach
(zobacz rysunek). Stosunek długości okręgów o środkach 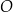 i
i 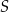 jest równy
jest równy  , a odcinek
, a odcinek 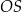 ma długość 24.
ma długość 24.
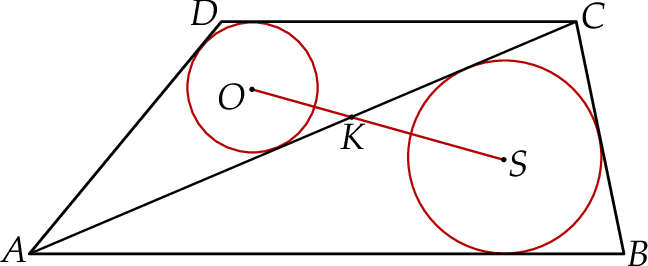
Wtedy
A) 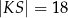 B)
B) 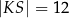 C)
C) 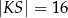 D)
D) 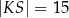
Przykładem liczby niewymiernej spełniającej nierówność 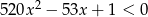 jest
jest
A) 0,04 B) 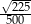 C)
C) 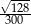 D)
D) 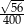
Zbiorem wszystkich rozwiązań równania 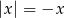 jest
jest
A) 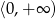 B)
B) 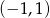 C)
C) 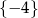 D)
D) 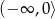
Zbiorem wszystkich rozwiązań równania 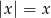 jest
jest
A) 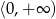 B)
B) 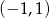 C)
C) 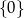 D)
D) 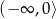
Cena towaru bez podatku VAT jest równa 60 zł. Towar ten wraz z podatkiem VAT w wysokości 22% kosztuje
A) 73,20 zł B) 49,18 zł C) 60,22 zł D) 82 zł
Cena towaru bez podatku VAT jest równa 90 zł. Towar ten wraz z podatkiem VAT w wysokości 23% kosztuje
A) 91,23 zł B) 110,7 zł C) 69,3 zł D) 105,13 zł
Wysokość graniastosłupa prawidłowego czworokątnego, którego pole powierzchni całkowitej jest równe 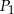 , zwiększono trzykrotnie. Pole powierzchni całkowitej otrzymanego w ten sposób graniastosłupa jest równe
, zwiększono trzykrotnie. Pole powierzchni całkowitej otrzymanego w ten sposób graniastosłupa jest równe 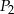 . Zatem
. Zatem
A) 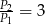 B)
B) 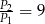 C)
C) 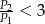 D)
D) 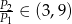
Rzucamy dwa razy symetryczną sześcienną kostką do gry. Prawdopodobieństwo dwukrotnego otrzymania liczby oczek różnej od 5 jest równe
A)  B)
B) 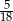 C)
C) 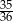 D)
D) 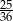
Liczba rzeczywista  spełnia warunek:
spełnia warunek: 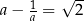 . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Wartość wyrażenia 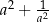 jest liczbą całkowitą. jest liczbą całkowitą. | P | F |
Liczba  jest liczbą wymierną. jest liczbą wymierną. | P | F |
Funkcja kwadratowa 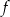 jest określona wzorem
jest określona wzorem 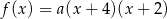 . Na rysunku przedstawiono fragment paraboli będącej wykresem tej funkcji. Jednym z punktów tej paraboli jest punkt
. Na rysunku przedstawiono fragment paraboli będącej wykresem tej funkcji. Jednym z punktów tej paraboli jest punkt 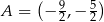 .
.
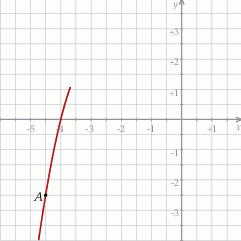
Najmniejsza wartość funkcji 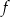 w przedziale
w przedziale 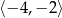 jest równa
jest równa
A) 0 B) 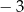 C)
C) 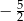 D)
D) 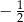
Do wykresu funkcji liniowej 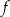 należy punkt
należy punkt 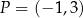 , a jej miejscem zerowym jest
, a jej miejscem zerowym jest 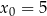 . Wzór funkcji
. Wzór funkcji 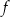 ma postać
ma postać
A) 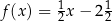 B)
B) 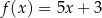 C)
C) 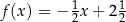 D)
D) 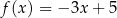
Miejscem zerowym funkcji liniowej 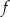 jest liczba 1. Wykres tej funkcji przechodzi przez punkt
jest liczba 1. Wykres tej funkcji przechodzi przez punkt 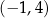 . Wzór funkcji
. Wzór funkcji 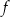 ma postać
ma postać
A) 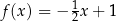 B)
B) 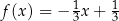
C) 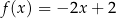 D)
D) 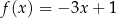
Miejscem zerowym funkcji liniowej 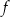 jest liczba
jest liczba 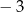 . Wykres tej funkcji przechodzi przez punkt
. Wykres tej funkcji przechodzi przez punkt 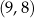 . Wzór funkcji
. Wzór funkcji 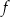 ma postać
ma postać
A) 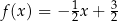 B)
B) 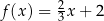
C) 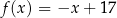 D)
D) 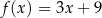
W okręgu 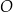 kąt środkowy
kąt środkowy 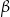 jest oparty na łuku trzy razy dłuższym od łuku, na którym oparty jest kąt wpisany
jest oparty na łuku trzy razy dłuższym od łuku, na którym oparty jest kąt wpisany  . Kąt
. Kąt 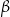 ma miarę o
ma miarę o 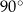 większą od kąta
większą od kąta  . Miara kąta
. Miara kąta 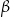 jest równa
jest równa
A) 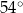 B)
B) 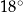 C)
C) 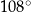 D)
D) 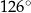
Który wyraz ciągu 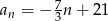 jest równy zero?
jest równy zero?
A) 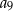 B)
B) 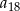 C)
C) 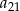 D)
D) 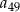
Układ równań 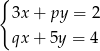 z niewiadomymi
z niewiadomymi  i
i 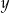 ma nieskończenie wiele rozwiązań. Zatem liczba
ma nieskończenie wiele rozwiązań. Zatem liczba 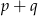 jest równa
jest równa
A) 6 B) 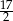 C)
C) 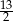 D) 15
D) 15
Układ równań 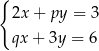 z niewiadomymi
z niewiadomymi  i
i 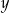 ma nieskończenie wiele rozwiązań. Zatem liczba
ma nieskończenie wiele rozwiązań. Zatem liczba 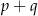 jest równa
jest równa
A) 6 B) 1 C) 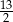 D)
D) 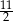
Obwód trójkąta 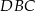 , przedstawionego na rysunku, jest równy
, przedstawionego na rysunku, jest równy
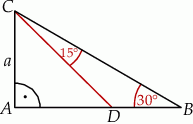
A) 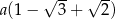 B)
B) 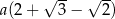 C)
C) 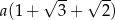 D)
D)