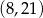Pięciowyrazowy ciąg 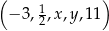 jest arytmetyczny. Liczby
jest arytmetyczny. Liczby  oraz
oraz 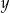 są równe
są równe
A) 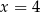 oraz
oraz 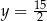 B)
B) 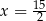 oraz
oraz 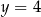
C) 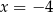 oraz
oraz 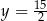 D)
D) 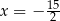 oraz
oraz 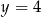
/Szkoła średnia/Zadania testowe
Pięciowyrazowy ciąg 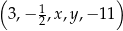 jest arytmetyczny. Liczby
jest arytmetyczny. Liczby  oraz
oraz 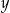 są równe
są równe
A) 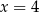 oraz
oraz 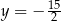 B)
B) 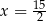 oraz
oraz 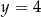
C) 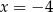 oraz
oraz 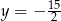 D)
D) 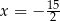 oraz
oraz 
Na rysunku zaznaczono długości niektórych odcinków w rombie oraz kąt  .
.
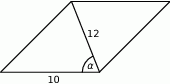
Wtedy
A) 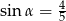 B)
B) 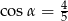 C)
C) 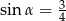 D)
D) 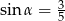
Na rysunku zaznaczono długości niektórych odcinków w rombie oraz kąt  .
.
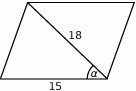
Wtedy
A) 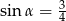 B)
B) 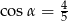 C)
C) 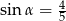 D)
D) 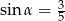
Funkcja 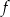 określona jest wzorem
określona jest wzorem 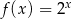 . Funkcja
. Funkcja 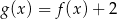 z prostą
z prostą 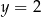
A) ma jeden punkt wspólny B) dwa punkty wspólne
C) nie ma punktów wspólnych D) ma nieskończenie wiele punktów wspólnych
Funkcja 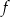 określona jest wzorem
określona jest wzorem 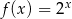 . Wykres funkcji
. Wykres funkcji 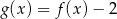 z prostą
z prostą 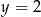
A) ma jeden punkt wspólny B) dwa punkty wspólne
C) nie ma punktów wspólnych D) ma nieskończenie wiele punktów wspólnych
Z prostopadłościanu 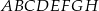 odcięto ostrosłup
odcięto ostrosłup 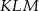 w ten sposób, że punkty
w ten sposób, że punkty 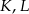 i
i 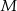 są środkami krawędzi
są środkami krawędzi 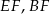 i
i 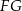 (zobacz rysunek).
(zobacz rysunek).
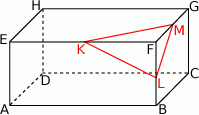
Ile razy objętość odciętego ostrosłupa jest mniejsza od objętości pozostałej części prostopadłościanu?
A) 48 razy. B) 47 razy. C) 46 razy. D) 24 razy.
Na ile sposobów można ustawić na półce 5 tomów encyklopedii tak, aby tomy 3 i 4 stały obok siebie (w dowolnej kolejności)?
A) 24 B) 48 C) 120 D) 60
Na ile sposobów można ustawić na półce 6 tomów encyklopedii tak, aby tomy 4, 5 i 6 stały obok siebie (w dowolnej kolejności)?
A) 144 B) 48 C) 72 D) 24
Z koła o promieniu 12 wycięto dwa wycinki odpowiadające kątom środkowym 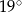 i
i 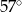 .
.
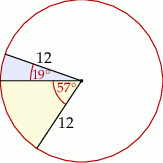
Następnie sklejono dwa stożki, których powierzchnie boczne utworzone zostały z otrzymanych wycinków. Ile razy pole podstawy większego z otrzymanych stożków jest większe od pola podstawy mniejszego stożka?
A) 3 B) 6 C) 9 D) 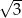
Wartość wyrażenia 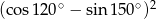 jest równa
jest równa
A) 1 B) 0 C) 3 D) 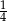
Wartość wyrażenia 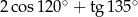 jest równa
jest równa
A) 2 B) 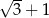 C)
C) 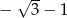 D)
D) 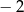
Wykres funkcji kwadratowej 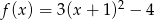 nie ma punktów wspólnych z prostą o równaniu
nie ma punktów wspólnych z prostą o równaniu
A) 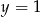 B)
B) 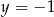 C)
C) 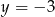 D)
D) 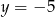
Wykres funkcji kwadratowej 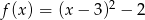 nie ma punktów wspólnych z prostą o równaniu
nie ma punktów wspólnych z prostą o równaniu
A) 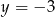 B)
B) 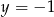 C)
C) 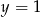 D)
D) 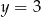
Wykres funkcji kwadratowej 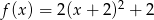 nie ma punktów wspólnych z prostą o równaniu
nie ma punktów wspólnych z prostą o równaniu
A) 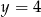 B)
B) 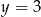 C)
C) 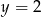 D)
D) 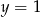
Na rysunkach poniżej przedstawiono siatki dwóch ostrosłupów.
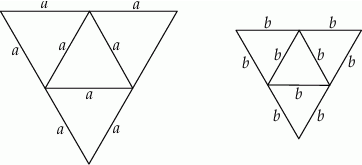
Pole powierzchni całkowitej ostrosłupa o krawędzi  jest dwa razy większe od pola powierzchni całkowitej ostrosłupa o krawędzi
jest dwa razy większe od pola powierzchni całkowitej ostrosłupa o krawędzi 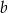 . Ile razy objętość ostrosłupa o krawędzi
. Ile razy objętość ostrosłupa o krawędzi  jest większa od objętości ostrosłupa o krawędzi
jest większa od objętości ostrosłupa o krawędzi 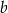 ?
?
A) 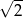 B) 2 C)
B) 2 C) 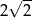 D) 4
D) 4
Na rysunkach poniżej przedstawiono siatki dwóch ostrosłupów.
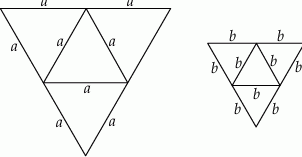
Pole powierzchni całkowitej ostrosłupa o krawędzi  jest trzy razy większe od pola powierzchni całkowitej ostrosłupa o krawędzi
jest trzy razy większe od pola powierzchni całkowitej ostrosłupa o krawędzi 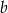 . Ile razy objętość ostrosłupa o krawędzi
. Ile razy objętość ostrosłupa o krawędzi  jest większa od objętości ostrosłupa o krawędzi
jest większa od objętości ostrosłupa o krawędzi 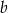 ?
?
A) 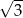 B)
B) 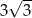 C) 3 D) 9
C) 3 D) 9
Odległość początku układu współrzędnych od prostej o równaniu 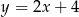 jest równa
jest równa
A) 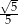 B)
B) 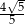 C)
C)  D) 4
D) 4
Odległość początku układu współrzędnych od prostej o równaniu 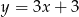 jest równa
jest równa
A) 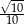 B)
B) 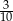 C)
C) 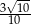 D) 3
D) 3
Odległość początku układu współrzędnych od prostej o równaniu 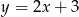 jest równa
jest równa
A) 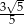 B)
B) 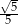 C)
C)  D) 3
D) 3
Odległość początku układu współrzędnych od prostej o równaniu 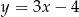 jest równa
jest równa
A) 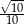 B) 4 C)
B) 4 C) 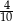 D)
D) 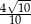
Odległość początku układu współrzędnych od prostej o równaniu 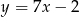 jest równa
jest równa
A) 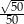 B)
B) 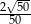 C)
C) 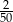 D) 2
D) 2
Odległość początku układu współrzędnych od prostej o równaniu 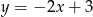 jest równa
jest równa
A) 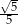 B) 3 C)
B) 3 C)  D)
D) 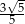
Punkt 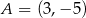 jest wierzchołkiem kwadratu
jest wierzchołkiem kwadratu 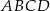 , a punkt
, a punkt 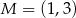 jest punktem przecięcia się przekątnych tego kwadratu. Wynika stąd, że pole kwadratu
jest punktem przecięcia się przekątnych tego kwadratu. Wynika stąd, że pole kwadratu 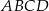 jest równe
jest równe
A) 68 B) 136 C) 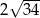 D)
D) 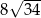
Punkt 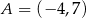 jest wierzchołkiem kwadratu
jest wierzchołkiem kwadratu 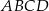 , a punkt
, a punkt 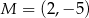 jest punktem przecięcia się przekątnych tego kwadratu. Wynika stąd, że pole kwadratu
jest punktem przecięcia się przekątnych tego kwadratu. Wynika stąd, że pole kwadratu 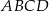 jest równe
jest równe
A) 360 B) 90 C) 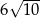 D)
D) 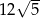
Funkcja 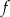 jest określona wzorem
jest określona wzorem 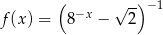 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Liczba
. Liczba 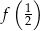 jest równa
jest równa
A) 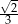 B)
B) 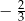 C)
C) 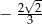 D)
D) 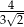
Przybliżenie z nadmiarem liczby dodatniej  wynosi 13. Błąd względny tego przybliżenia wynosi
wynosi 13. Błąd względny tego przybliżenia wynosi 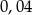 . Wobec tego
. Wobec tego
A) 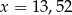 B)
B) 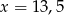 C)
C) 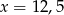 D)
D) 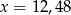
Przybliżenie z nadmiarem liczby dodatniej  wynosi 63. Błąd względny tego przybliżenia wynosi 0,008. Wobec tego
wynosi 63. Błąd względny tego przybliżenia wynosi 0,008. Wobec tego
A) 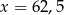 B)
B) 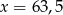 C)
C) 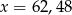 D)
D) 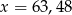
Przybliżenie z niedomiarem liczby  jest równe 6, a błąd względny tego przybliżenia wynosi 0,2. Wówczas liczba
jest równe 6, a błąd względny tego przybliżenia wynosi 0,2. Wówczas liczba  jest równa:
jest równa:
A) 4,8 B) 5 C) 7,2 D) 7,5
Przybliżenie z nadmiarem liczby dodatniej  wynosi 16. Błąd względny tego przybliżenia wynosi 0,024. Wobec tego
wynosi 16. Błąd względny tego przybliżenia wynosi 0,024. Wobec tego
A) 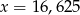 B)
B) 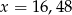 C)
C) 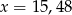 D)
D) 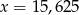
Przybliżenie z niedomiarem liczby dodatniej  wynosi 18. Błąd względny tego przybliżenia wynosi 0,04. Wobec tego
wynosi 18. Błąd względny tego przybliżenia wynosi 0,04. Wobec tego
A) 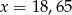 B)
B) 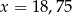 C)
C) 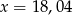 D)
D) 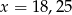
Kasia kupiła dwa i pół kilograma landrynek po 20 zł za kilogram, pół kilograma cukierków czekoladowych po 14 zł za kilogram i kilogram cukierków kawowych po 15 zł za kilogram. Średnia wartość 1 kg cukierków, które kupiła Kasia, była równa
A) 18 zł B) ok. 16,30 zł C) 24 zł D) 23 zł
Ewa kupiła trzy i pół kilograma landrynek po 16 zł za kilogram, dwa i pół kilograma cukierków czekoladowych po 12 zł za kilogram i dwa kilogramy cukierków kawowych po 11 zł za kilogram. Średnia wartość 1 kg cukierków, które kupiła Kasia, była równa
A) 13 zł B) 14 zł C) 13,5 zł D) 14,2 zł
Jacek kupił pół kilograma landrynek po 18 zł za kilogram, dwa i pół kilograma cukierków czekoladowych po 16 zł za kilogram i kilogram cukierków kawowych po 13 zł za kilogram. Średnia wartość 1 kg cukierków, które kupił Jacek, była równa
A) 15,50 zł B) 16,30 zł C) 23,50 zł D) 17,20 zł
Odcinek 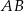 jest średnicą okręgu o środku w punkcie
jest średnicą okręgu o środku w punkcie 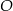 i promieniu
i promieniu 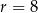 (zobacz rysunek). Cięciwa
(zobacz rysunek). Cięciwa 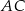 ma długość
ma długość 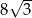 .
.
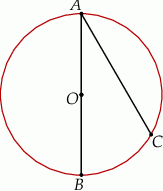
Miara kąta 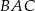 jest równa
jest równa
A) 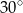 B)
B) 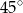 C)
C) 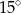 D)
D) 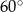
Odcinek 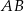 jest średnicą okręgu o środku w punkcie
jest średnicą okręgu o środku w punkcie 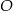 i promieniu
i promieniu 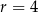 (zobacz rysunek). Cięciwa
(zobacz rysunek). Cięciwa 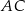 ma długość
ma długość 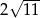 .
.
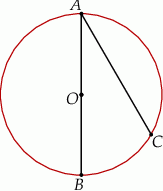
Sinus kąta 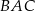 jest równy
jest równy
A) 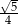 B)
B) 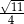 C)
C) 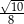 D)
D) 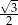
Rozwinięcie dziesiętne nieskończone ma liczba
A) 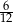 B)
B) 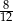 C)
C) 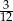 D)
D) 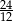
Rozwinięcie dziesiętne nieskończone ma liczba
A) 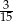 B)
B) 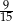 C)
C) 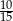 D)
D) 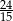
Rozwinięcie dziesiętne nieskończone ma liczba
A) 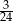 B)
B) 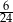 C)
C) 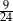 D)
D) 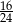
Funkcja liniowa 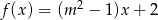 jest rosnąca wtedy, gdy
jest rosnąca wtedy, gdy
A) 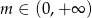 B)
B) 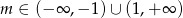 C)
C) 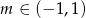 D)
D) 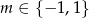
Funkcja liniowa 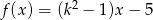 jest malejąca dla
jest malejąca dla
A) 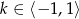 B)
B) 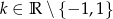 C)
C) 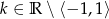 D)
D) 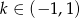
Funkcja liniowa 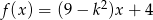 jest rosnąca wtedy, gdy
jest rosnąca wtedy, gdy
A) 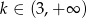 B)
B) 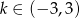 C)
C) 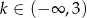 D)
D) 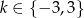
Funkcja liniowa 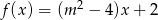 jest malejąca, gdy
jest malejąca, gdy
A) 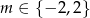 B)
B) 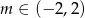 C)
C) 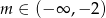 D)
D) 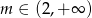
Funkcja liniowa 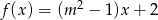 jest malejąca wtedy, gdy
jest malejąca wtedy, gdy
A) 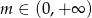 B)
B) 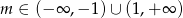 C)
C) 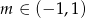 D)
D) 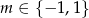
Wszystkich liczb naturalnych dwucyfrowych, które są podzielne przez 6 lub przez 10, jest
A) 25 B) 24 C) 21 D) 20
Wszystkich liczb naturalnych dwucyfrowych, które są podzielne przez 8 lub przez 20, jest
A) 13 B) 15 C) 22 D) 44
Wszystkich liczb naturalnych dwucyfrowych, które są podzielne przez 7 lub przez 10, jest
A) 24 B) 21 C) 23 D) 22
W pewnym liceum 85% uczniów posiada telefony komórkowe. Pozostałych 27 uczniów nie posiada telefonów komórkowych. Wobec tego telefony posiada
A) mniej niż 160 osób B) więcej niż 200 osób C) 180 osób D) 154 osoby
W pewnej szkole 75% uczniów mieszka w internacie. Pozostałych 105 uczniów dojeżdża do szkoły autobusem. Wobec tego w internacie mieszka
A) mniej niż 300 uczniów B) więcej niż 400 uczniów C) 315 uczniów D) 210 uczniów.
Punkty 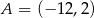 ,
, 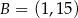 i
i 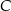 leżą na jednej prostej. Punkt
leżą na jednej prostej. Punkt 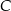 może mieć współrzędne
może mieć współrzędne
A) 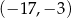 B)
B) 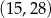 C)
C) 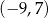 D)
D)